Содержание
- 2. доцент кафедры математического образования Батан Любовь Федоровна учитель математики первой квалификационной категории МОУ лицей № 176
- 3. Аннотация Урок алгебры рекомендован для учащихся 10 класса, обучающихся по учебнику «Алгебра и математический анализ» для
- 4. Актуальность Данная тема является очень важной и значимой, т. к. в материалах ЕГЭ большое внимание уделяется
- 5. Тип урока Урок закрепления изученного материала в форме самостоятельной групповой работы по карточкам Оборудование: Smart-доска; Сканер;
- 6. Цели урока Для учителя Для ученика
- 7. Цели урока Обобщить и закрепить свои знания и умения при построении графика функции с помощью ее
- 8. Цели урока Систематизировать, обобщить и расширить знания и умения учащихся при построении графиков функций. Развивать умения
- 9. Задачи урока Формировать устойчивый интерес к математике через дифференцированный подход к учащимся. Вовлекать каждого ученика в
- 10. Содержание урока Вводная беседа. Устная работа. Самостоятельная работа в группах. Обобщение. Итог. Историческая справка. Рефлексия.
- 11. На уроке мы должны закрепить и обобщить свои знания и умения при построении графика функции с
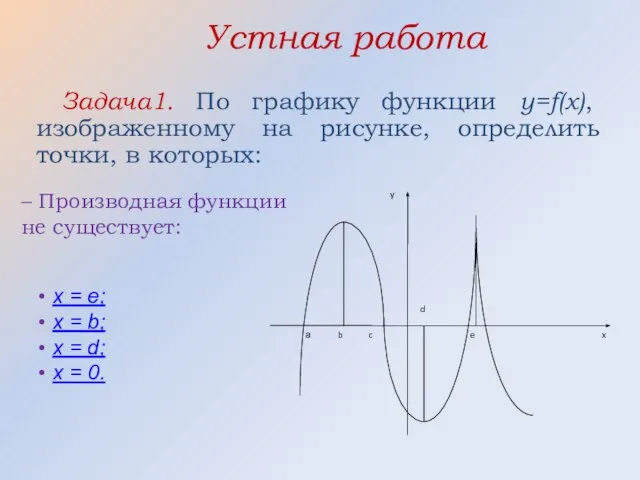
- 12. Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить точки, в которых: – Производная
- 13. Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить точки, в которых: – Производная
- 14. Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить: – Точки максимума функции: x
- 15. Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить: – промежутки убывания функции: [b;d]
- 16. Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить: – Промежутки возрастания функции: [b;d]
- 17. Отлично! Далее
- 18. Подумай ещё!
- 19. Отлично! Далее
- 20. Подумай ещё!
- 21. Отлично! Далее
- 22. Подумай ещё!
- 23. Отлично! Далее
- 24. Подумай ещё!
- 25. Отлично! Далее
- 26. Подумай ещё!
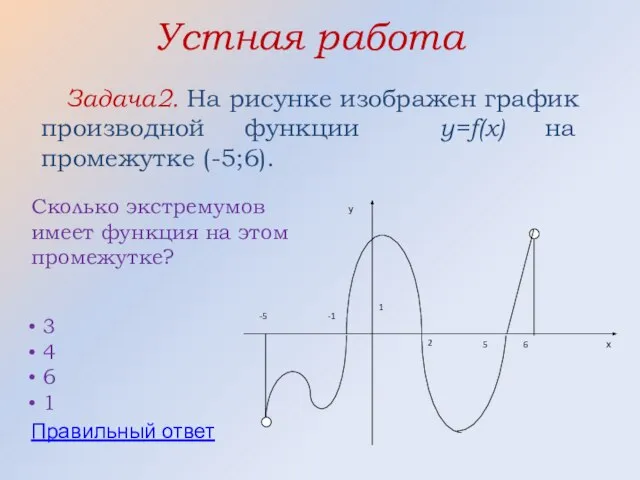
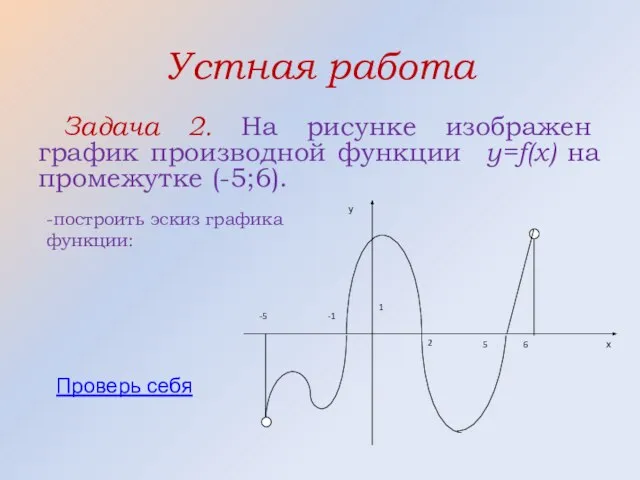
- 27. Устная работа Задача2. На рисунке изображен график производной функции y=f(x) на промежутке (-5;6). Сколько экстремумов имеет
- 28. Правильный ответ 3
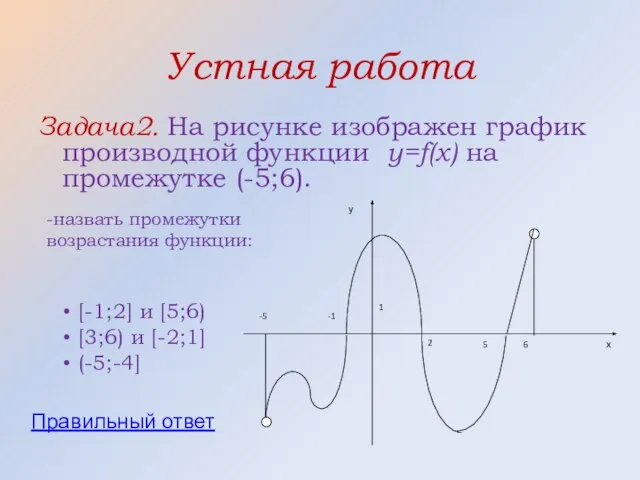
- 29. Устная работа Задача2. На рисунке изображен график производной функции y=f(x) на промежутке (-5;6). -назвать промежутки возрастания
- 30. Правильный ответ [-1;2] и [5;6)
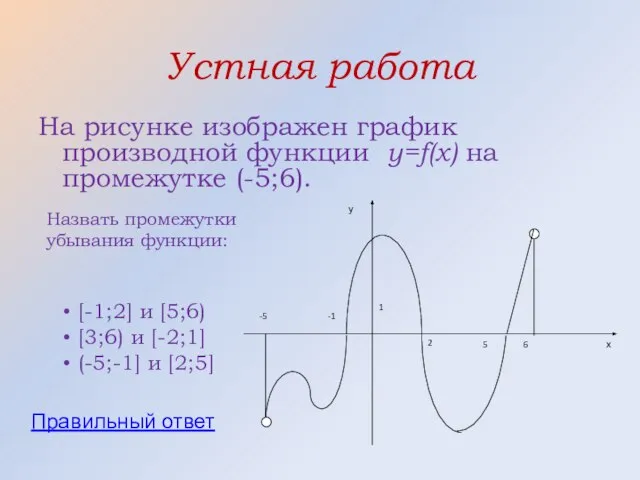
- 31. Устная работа На рисунке изображен график производной функции y=f(x) на промежутке (-5;6). Назвать промежутки убывания функции:
- 32. Правильный ответ (-5;-1] и [2;5]
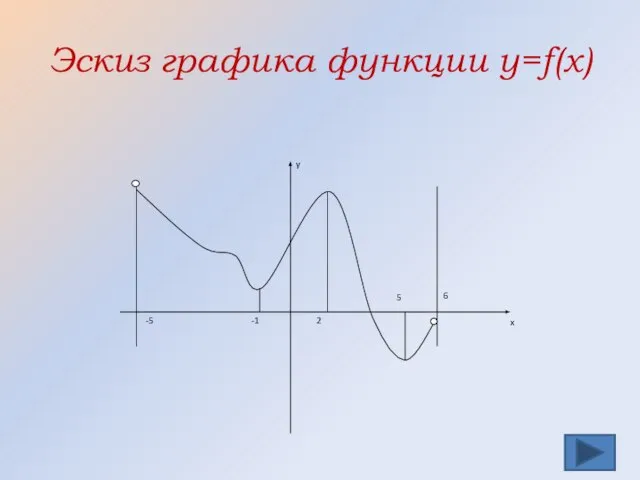
- 33. Устная работа Задача 2. На рисунке изображен график производной функции y=f(x) на промежутке (-5;6). -построить эскиз
- 34. Эскиз графика функции y=f(x)
- 35. Устная работа Задача3. Найти асимптоты графика функции Проверь себя
- 36. Ответ х=2 – вертикальная асимптота у=х – наклонная асимптота
- 37. Самостоятельная работа учащихся Класс делится на 3 группы. Каждая группа учащихся получает задание на карточке. Первая
- 38. Уровни базовый уровень основной уровень продвинутый уровень
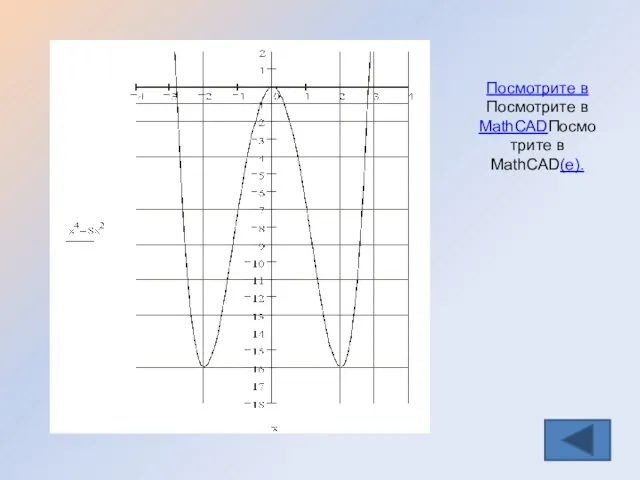
- 39. Задание группе 1 Базовый уровень: Исследовать функцию и построить ее график у = x4 – 8x2
- 40. Задание группе 2 Основной уровень: Исследовать функцию и построить ее график Проверь себя Назад Справка
- 41. Задание группе 3 Продвинутый уровень: Исследовать функцию и построить ее график Проверь себя Назад Справка
- 42. Вспомните план исследования: 1.Область определения функции. 2.Множество значений функции. 3.Чётность. 4.Периодичность. 5.Первая производная: по ней определяются
- 43. Вспомните план исследования: 1.Область определения функции. 2.Множество значений функции. 3.Чётность. 4.Периодичность. 5.Первая производная: по ней определяются
- 44. Вспомните план исследования: 1.Область определения функции. 2.Множество значений функции. 3.Чётность. 4.Периодичность. 5.Первая производная: по ней определяются
- 45. Проверь себя Замечаем, что функция четная и ее график симметричен оси ОУ, достаточно исследовать ее на
- 46. Посмотрите в Посмотрите в MathCADПосмотрите в MathCAD(е).
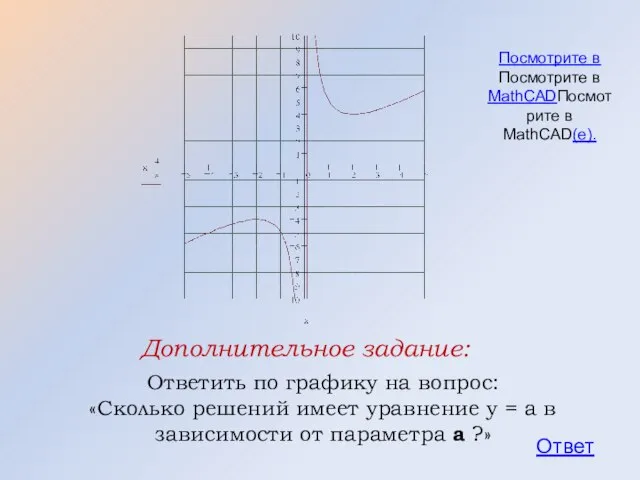
- 47. Ответить, используя график, на вопросы: 1. Сколько критических точек имеет функция ? 2. Чему равна точка
- 48. Ответить, используя график, на вопросы: 1. Сколько критических точек имеет функция ? ( 3 ) 2.
- 49. Ответить по графику на вопрос: «Сколько решений имеет уравнение у = а в зависимости от параметра
- 50. Ответ: Если а = ± 4, то одно решение. Если |а| > 4, то два решения.
- 51. Обобщение Графики функций можно строить «по точкам». Однако при таком способе построения можно пропустить важные особенности
- 52. Итог Вот что сказал Декарт по поводу методов: «Под методом же я разумею точные и простые
- 53. Математика развивалась стремительно, но без понятия производной многие исследования не имели смысла. В 1679 году Пьер
- 54. Исследуя функцию с помощью производной, я научился находить : Область определения функции; Определять четность функции; Критические
- 55. Спасибо за урок До свидания!!! Удачи вам!!!
- 57. Скачать презентацию

























![Правильный ответ [-1;2] и [5;6)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/285813/slide-29.jpg)
![Правильный ответ (-5;-1] и [2;5]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/285813/slide-31.jpg)



















 На лесной поляне
На лесной поляне Показательная функция. Теория
Показательная функция. Теория Презентация на тему ИСПОЛЬЗОВАНИЕ МЕТОДИКИ РАЗВИВАЮЩЕГО ОБУЧЕНИЯ НА УРОКАХ МАТЕМАТИКИ
Презентация на тему ИСПОЛЬЗОВАНИЕ МЕТОДИКИ РАЗВИВАЮЩЕГО ОБУЧЕНИЯ НА УРОКАХ МАТЕМАТИКИ  Умножение. Законы умножения
Умножение. Законы умножения Цилиндр. Сечения цилиндра
Цилиндр. Сечения цилиндра Методы доказательства теорем: прямой метод и метод от противного
Методы доказательства теорем: прямой метод и метод от противного Самостоятельная работа. Задания
Самостоятельная работа. Задания Задачи по геометрии 11 класс
Задачи по геометрии 11 класс Центральная симметрия
Центральная симметрия Правильные и неправильные дроби
Правильные и неправильные дроби Щенок Пузырёк. Сложение и вычитание в пределах десяти
Щенок Пузырёк. Сложение и вычитание в пределах десяти Дифференциалы высших порядков
Дифференциалы высших порядков Устный счёт. Математика
Устный счёт. Математика 2.7. Теория систем линейных алгебраических уравнений
2.7. Теория систем линейных алгебраических уравнений Первообразная
Первообразная Тренажёр. Игра Хоккей
Тренажёр. Игра Хоккей Таблица умножения
Таблица умножения Интервальные вычисления. Лекция 11
Интервальные вычисления. Лекция 11 Уравнение средней
Уравнение средней 제1장 통계와 통계학
제1장 통계와 통계학 Дифференциальные уравнения и их применение в медицине
Дифференциальные уравнения и их применение в медицине Հեղուկների և գազերի կիռարական մեխանիկա
Հեղուկների և գազերի կիռարական մեխանիկա The formal normal form degenerate singular points in the case of case of focus
The formal normal form degenerate singular points in the case of case of focus Математический ребус
Математический ребус Измерение размеров деталей с помощью штангенциркуля
Измерение размеров деталей с помощью штангенциркуля Презентация на тему СВОЙСТВА ДВИЖЕНИЯ
Презентация на тему СВОЙСТВА ДВИЖЕНИЯ  Старинные меры длины
Старинные меры длины Числовая последовательность
Числовая последовательность