«слово», «отношение» и ἀριθμός — «число») и переводится как отношение чисел, одно из которых является членом арифметической прогрессии, а другое членом геометрической прогрессии.
В первые это понятие ввел английский математик Джон Непер,
о чем сообщалось в публикации 1614 года.
Кроме того, этот человек известен тем, что он первый изобрел
таблицу логарифмов, которая пользовалась большой популяр-
ностью среди ученых на протяжении долгих лет.
Первые таблицы десятичных логарифмов были составлены в
1617 г. английским математиком Бриггсом.
Изобретатели логарифмов не ограничились созданием
логарифмических таблиц, уже через 9 лет после их разработки в 1623 г. английским математиком Гантером была создана первая логарифмическая линейка. Она стала рабочим инструментом для многих поколений инженеров (до 70-х годов нашего века). В настоящее время значения логарифмов находят используя компьютер.
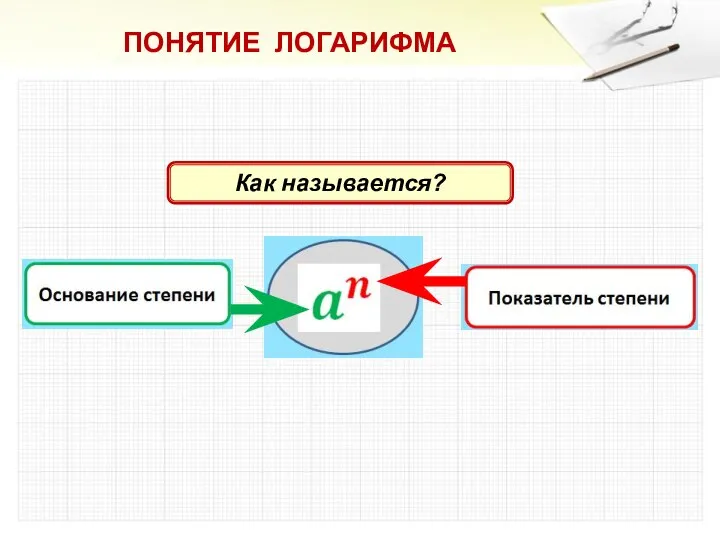
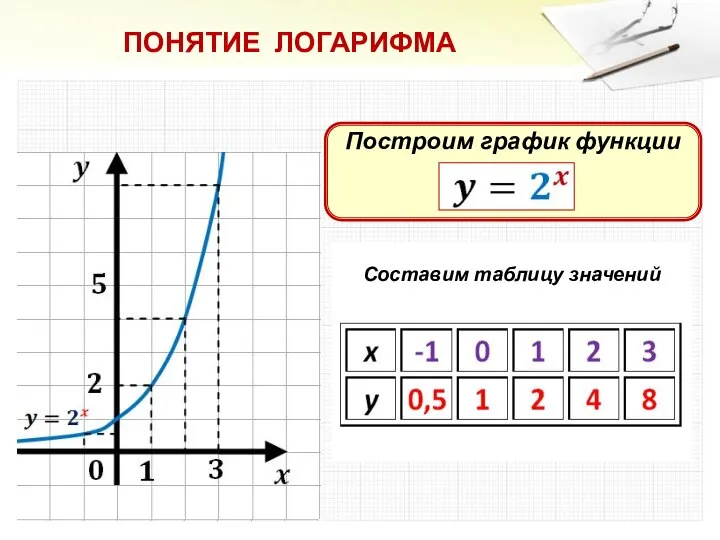
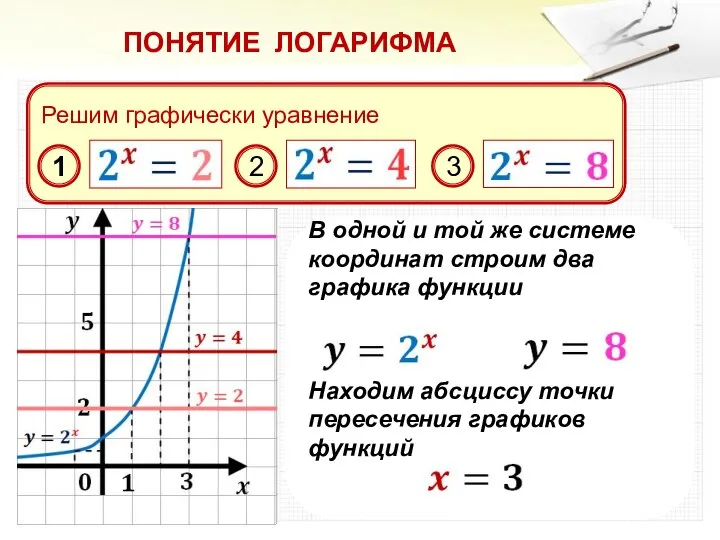
ПОНЯТИЕ ЛОГАРИФМА












 Сводка и группировка
Сводка и группировка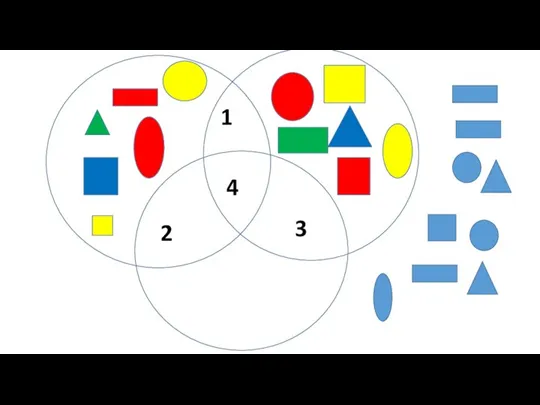 Круги Эйлера. Геометрические фигуры
Круги Эйлера. Геометрические фигуры Проект Колодец. Деловая игра по теме Цилиндр
Проект Колодец. Деловая игра по теме Цилиндр Погрешности измерений
Погрешности измерений Буквенные выражения
Буквенные выражения Задачи. вариант 3
Задачи. вариант 3 Индивидуальный итоговый проект по математике 22 задание ОГЭ
Индивидуальный итоговый проект по математике 22 задание ОГЭ Площадь трапеции
Площадь трапеции Математика. Исправляем ошибки
Математика. Исправляем ошибки Площади и объемы
Площади и объемы Случаи вычитания 15-
Случаи вычитания 15- Производная. Определение производной
Производная. Определение производной Презентация на тему Свойства степени с рациональным показателем
Презентация на тему Свойства степени с рациональным показателем  Сложение однозначных чисел с переходом через десяток вида * + 6
Сложение однозначных чисел с переходом через десяток вида * + 6 Касательная к окружности. 7 класс
Касательная к окружности. 7 класс Аналитическая геометрия. Уравнения прямой
Аналитическая геометрия. Уравнения прямой Формулы половинного аргумента
Формулы половинного аргумента Веселый счет (Счет в прямом и обратном порядке в пределах 10)
Веселый счет (Счет в прямом и обратном порядке в пределах 10) ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ
ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ Презентация на тему Аксиома параллельных прямых
Презентация на тему Аксиома параллельных прямых  Арифметические действия
Арифметические действия Основные задачи и область применения дискретной математики
Основные задачи и область применения дискретной математики Презентация на тему Длина отрезка
Презентация на тему Длина отрезка  Соотношения между тригонометрическими функциями одного аргумента
Соотношения между тригонометрическими функциями одного аргумента Геометрия до Евклида
Геометрия до Евклида Магические цифры
Магические цифры Регрессионный анализ
Регрессионный анализ Подобие треугольников
Подобие треугольников