Тела вращения

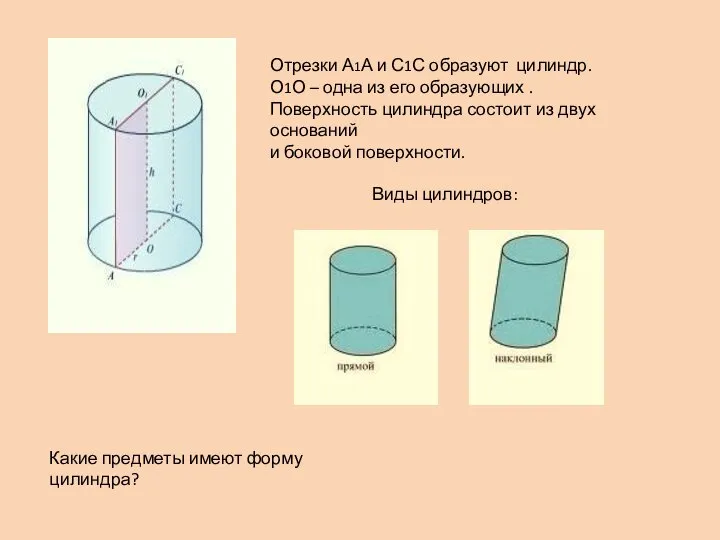
Отрезки А1А и С1С образуют цилиндр.
О1О – одна из его образующих .
Поверхность цилиндра состоит из двух оснований
и боковой поверхности.
Какие предметы имеют форму цилиндра?
Виды цилиндров:

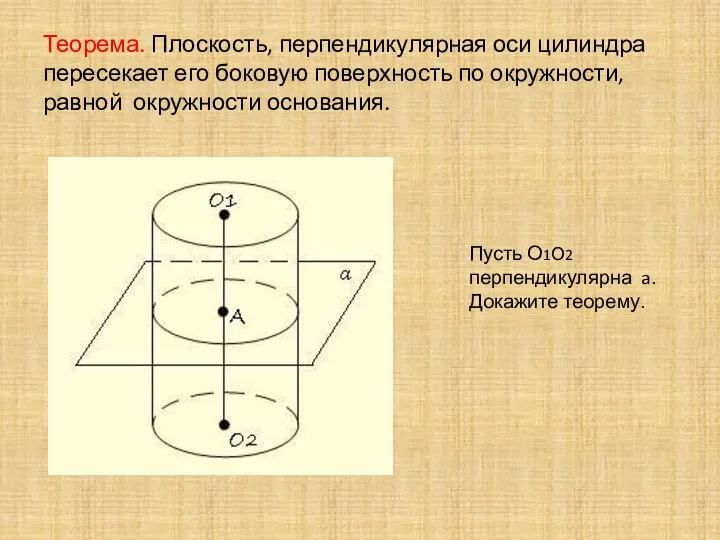
Теорема. Плоскость, перпендикулярная оси цилиндра пересекает его боковую поверхность по окружности, равной окружности основания.
Пусть О1О2 перпендикулярна a.
Докажите теорему.

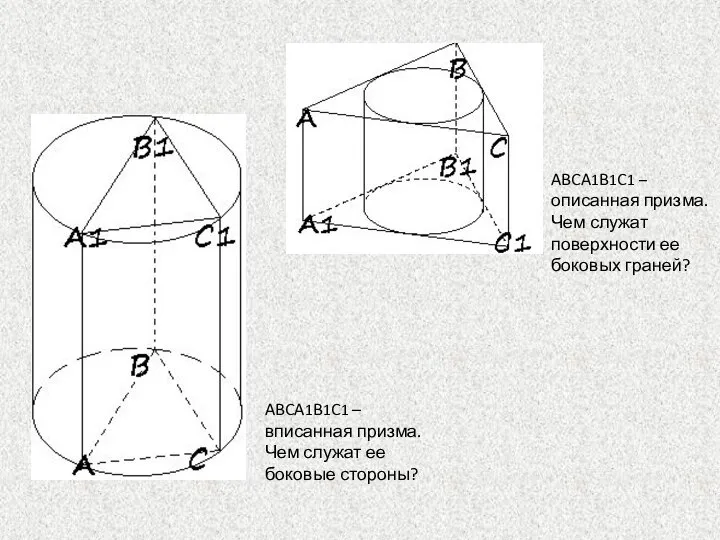
ABCA1B1C1 – вписанная призма.
Чем служат ее боковые стороны?
ABCA1B1C1 – описанная призма.
Чем служат поверхности ее боковых граней?

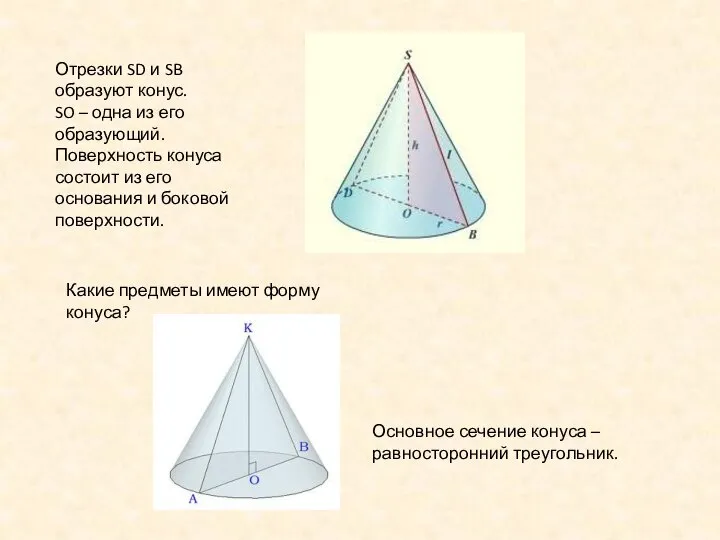
Отрезки SD и SB образуют конус.
SO – одна из его образующий.
Поверхность конуса состоит из его основания и боковой поверхности.
Какие предметы имеют форму конуса?
Основное сечение конуса – равносторонний треугольник.

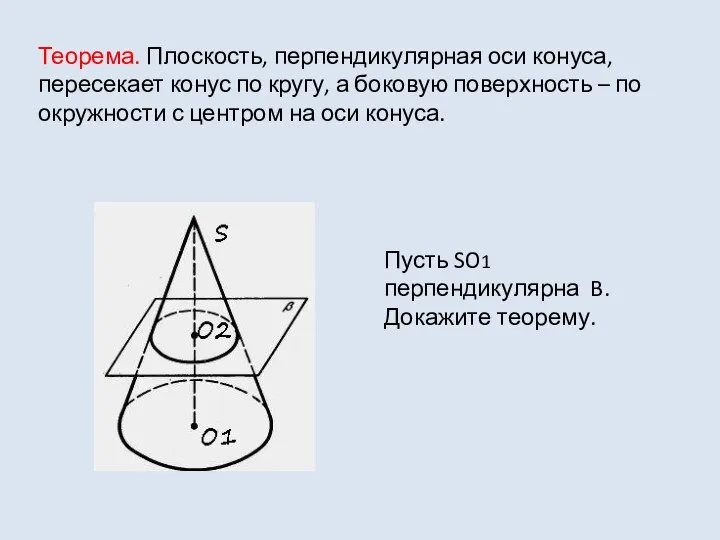
Теорема. Плоскость, перпендикулярная оси конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса.
Пусть SO1 перпендикулярна B.
Докажите теорему.

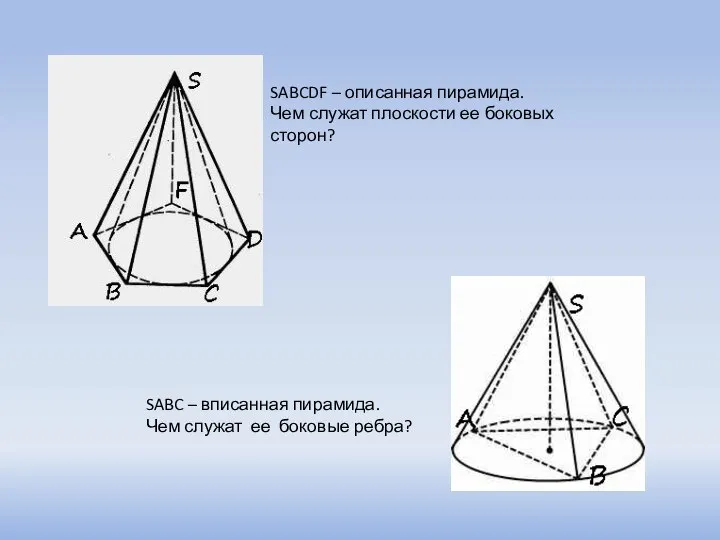
SABCDF – описанная пирамида.
Чем служат плоскости ее боковых сторон?
SABC – вписанная пирамида.
Чем служат ее боковые ребра?

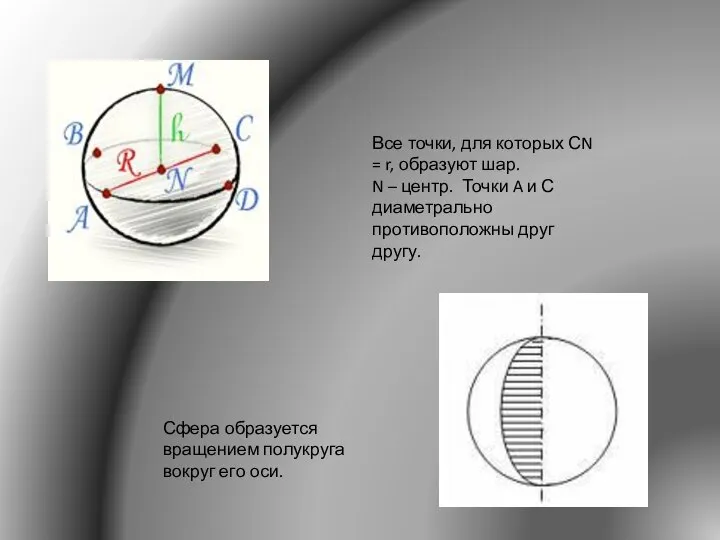
Все точки, для которых СN = r, образуют шар.
N – центр. Точки A и С диаметрально противоположны друг другу.
Сфера образуется вращением полукруга вокруг его оси.

Теорема. Всякое сечение шара плоскостью – круг. Центр этого круга – основание перпендикуляра опущенного из центра шара на секущую плоскость.
Пусть А принадлежит шару с радиуса R и плоскости a. OB перпендикулярно плоскости a.
Доказать теорему.
Показать, что всякая точка этого круга принадлежит шару.

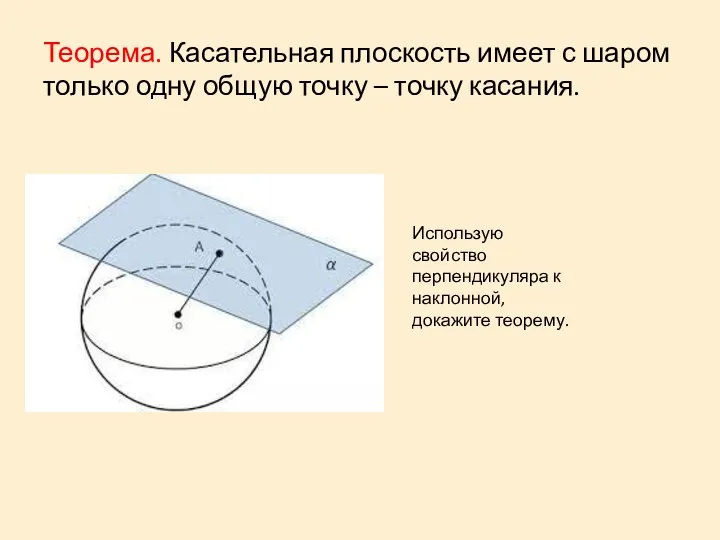
Теорема. Касательная плоскость имеет с шаром только одну общую точку – точку касания.
Использую свойство перпендикуляра к наклонной, докажите теорему.

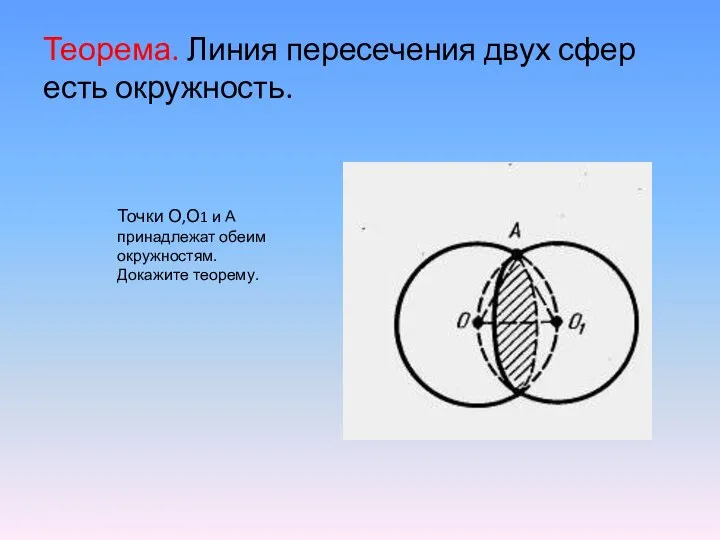
Теорема. Линия пересечения двух сфер есть окружность.
Точки О,О1 и А принадлежат обеим окружностям.
Докажите теорему.

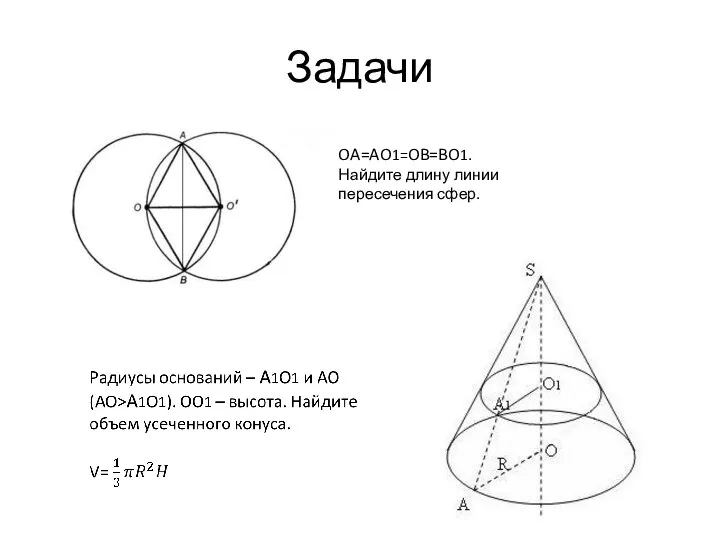
Задачи
OA=AO1=OB=BO1.
Найдите длину линии пересечения сфер.