Содержание
- 2. Цели урока: Ввести определение показательного уравнения; Рассмотреть методы решения показательных уравнений. Подготовиться к заданиям В3, встречающиеся
- 3. А мы умеем устно считать! Вспомним! Изучение нового. Давайте решать!. Рефлексия. Итог урока. Сегодня нас ожидает…
- 4. Устный счет. 3. Решите уравнения. Ответ: А) 3; Ответ: Б) 2; Ответ: В) 4; Ответ: Г)
- 5. Актуализация знаний. 1.Среди заданных функций укажите те, которые являются показательными: Ответ: А); В). 2.Какие из заданных
- 6. Пример 1.
- 7. Изучение нового материала Показательное уравнение-это уравнение, содержащее неизвестное в показателе степени при некоторых постоянных основаниях. Примеры
- 8. I. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ Определение: показательными уравнениями называются уравнения вида a f(x) = a g(x) , где
- 9. Методы решения показательных уравнений: 1. Метод уравнивания показателей; 2. Метод введения новой переменной. 3.Метод вынесения общего
- 10. I. Метод уравнивания показателей 2 2 х –4 = 2 6 2 х – 4 =
- 11. II. Метод введения новой переменной. Решить уравнение : 4х + 2 х+1 – 24 = 0
- 12. III. Метод вынесения общего множителя за скобки. Решите уравнение Ответ: х=1
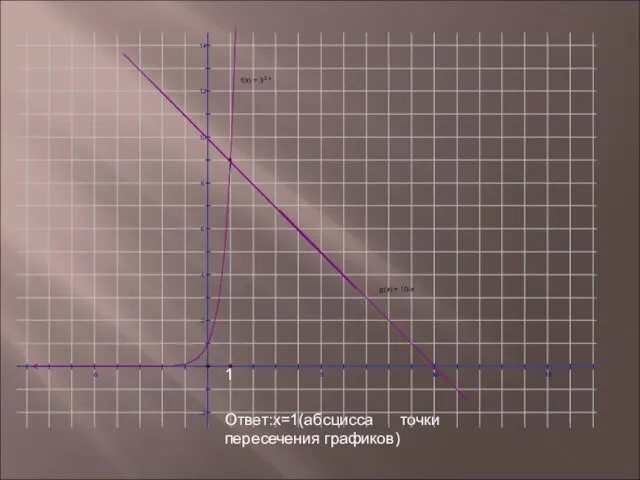
- 13. Использование графического метода решения уравнений. Решить уравнение Построим таблицы значений.
- 14. Ответ:х=1(абсцисса точки пересечения графиков)
- 15. Работа в группах:
- 16. Синквейн Это стихотворение, представляющее собой синтез информации в лаконичной форме
- 17. Синквейн 1 строка – заявляется тема или предмет (одно существительное) 2 строка – описание предмета (два
- 18. Пример 1. Экзамен. 2. Строгий, трудный. 3. Проверяет, доказывает, подтверждает 4. Что ты знаешь, а чего
- 19. Примеры Сумму квадратов катетов – мы знаем, Квадрат гипотенузы – вычисляем, Корень квадратный из неё извлекаем
- 20. Подведём итог Сегодня на уроке Я узнал… Сегодня на уроке Я научился…
- 21. Домашнее задание: Учебник П36, № 460 (а,г) , 461(а,б) Рабочая тетрадь В3 с. 28-29 № Т9.1,
- 23. Скачать презентацию



















 Сложение и вычитание с переходом через десяток в пределах 10. Интерактивная игра-тренажер по математике Смешарики
Сложение и вычитание с переходом через десяток в пределах 10. Интерактивная игра-тренажер по математике Смешарики Факториал. Задача со стульями
Факториал. Задача со стульями Повторение. Дроби
Повторение. Дроби В стране занимательной Математики
В стране занимательной Математики Понятие функции. Свойства функции
Понятие функции. Свойства функции Многочлен. Основные понятия. Определение многочлена
Многочлен. Основные понятия. Определение многочлена Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Решение задач по теме Длина окружности, длина дуги окружности
Решение задач по теме Длина окружности, длина дуги окружности Квадратичная функция
Квадратичная функция Устно вычислите значение производной
Устно вычислите значение производной Путешествие в город Дробей на проспект Умножения. 6 класс
Путешествие в город Дробей на проспект Умножения. 6 класс Многогранники и их основные свойства
Многогранники и их основные свойства Признаки параллельности прямых
Признаки параллельности прямых Задача о железнодорожных составах
Задача о железнодорожных составах Схемы к задачам
Схемы к задачам Формула перехода к новому основанию логарифма
Формула перехода к новому основанию логарифма Асимптоты. Вертикальная асимптота
Асимптоты. Вертикальная асимптота Готовимся к ЕГЭ-2015 по математике. Решение 1 части реального теста ЕГЭ-2014
Готовимся к ЕГЭ-2015 по математике. Решение 1 части реального теста ЕГЭ-2014 Животные в мире математики
Животные в мире математики Решение и составление ребусов
Решение и составление ребусов Отношения. Синонимы в русском языке и математике
Отношения. Синонимы в русском языке и математике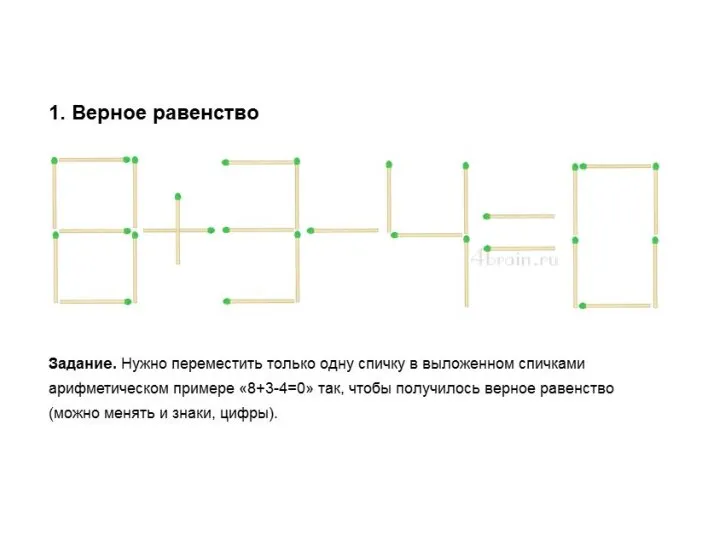 Спички
Спички Многозначные числа. Тест
Многозначные числа. Тест Определение корня n–ой степени
Определение корня n–ой степени pokaz_ur-nia
pokaz_ur-nia Треугольники. Решение задач
Треугольники. Решение задач Решение линейных неравенств
Решение линейных неравенств Векторы. Метод координат
Векторы. Метод координат