Понятие о производной функции

Свободно падающее тело за время t проходит расстояние
Найти мгновенную скорость тела в момент времени t, если
S= 20 м g≈10 м/с2
Задача №1

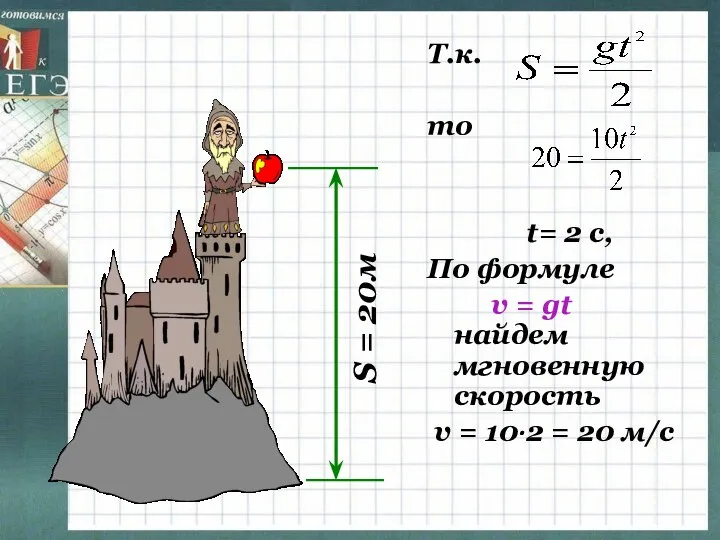
S = 20м
Т.к.
то
t= 2 с,
По формуле
v = gt найдем мгновенную скорость
v = 10·2 = 20 м/с

По прямой, на которой заданы начало отсчета, единица измерения (метр) и направление, движется некоторое тело (материальная точка). Закон движения задан формулой S=S(t), где t – время (в секундах), S(t) – положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу отсчета (в метрах). Найти скорость движения тела в момент времени t (в м/с).
Задача №2

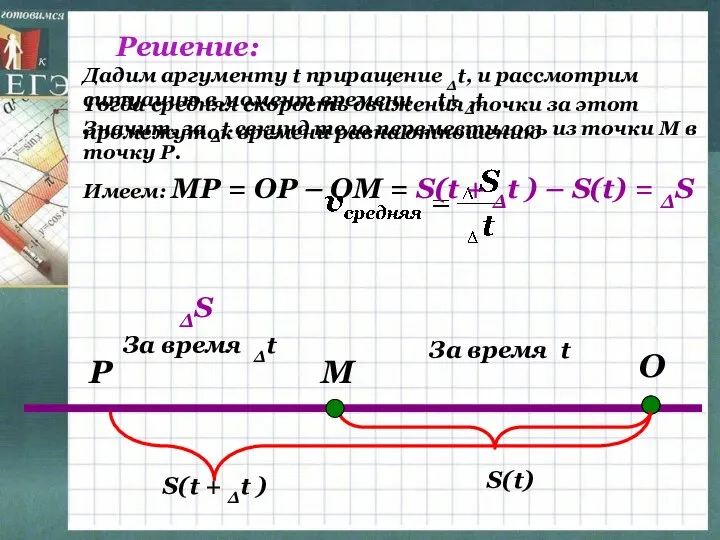
Решение:
S(t)
За время t
Дадим аргументу t приращение Δt, и рассмотрим ситуацию в момент времени t+ Δt
S(t + Δt )
Тогда средняя скорость движения точки за этот промежуток времени равна отношению
За время Δt
О
М
Р
Значит, за Δt секунд тело переместилось из точки М в точку Р.
∆S
Имеем: МР = ОР – ОМ = S(t + Δt ) – S(t) = ∆S

Рассмотрим, как связаны между собой средняя и мгновенная скорости движения:
S(t)
S(t + Δt )
Что такое скорость v(t) в момент времени (ее называют мгновенной скоростью )?
Это средняя скорость движения за промежуток времени Δt, при условии, что Δt выбирается все меньше и меньше; точнее при условии, что Δt → 0.
Δt → 0
Число v(t) называют пределом данного отношения при ∆t→ 0
∆S

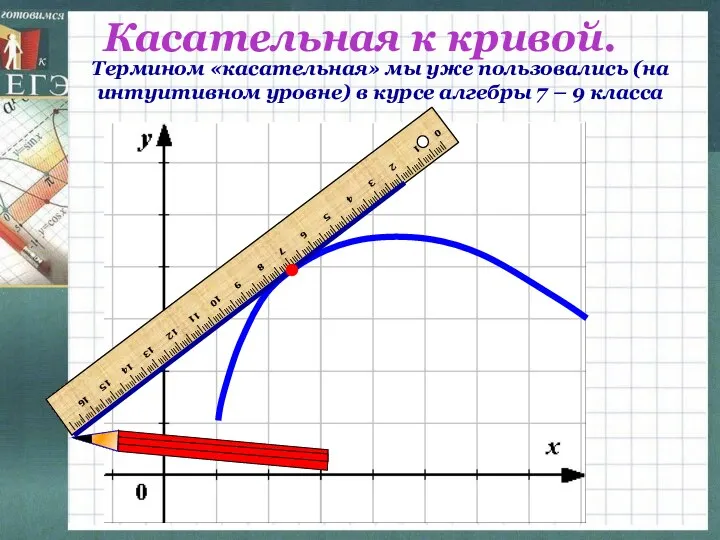
Касательная к кривой.
Термином «касательная» мы уже пользовались (на интуитивном уровне) в курсе алгебры 7 – 9 класса

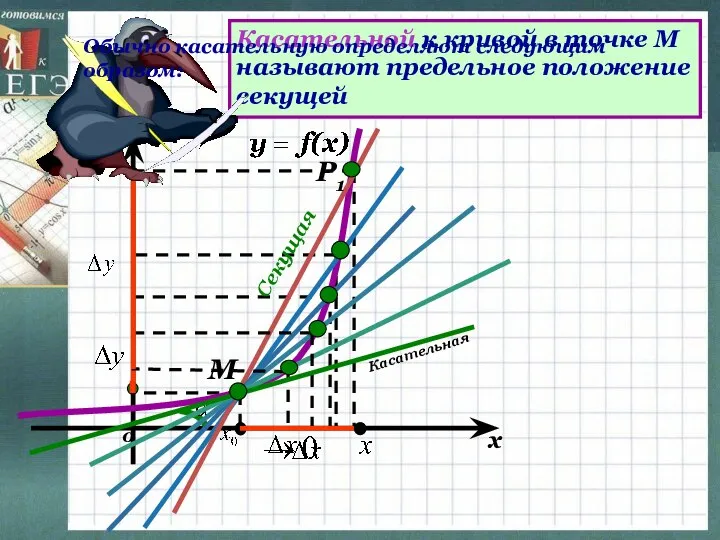
Секущая
М
Р1
Касательной к кривой в точке М называют предельное положение секущей
Обычно касательную определяют следующим образом:

Дан график функции у = f(x). На нем выбрана точка М(а; f(a)), в этой точке к графику функции проведена касательная (предполагается, что она существует). Найти угловой коэффициент касательной.
Задача №3

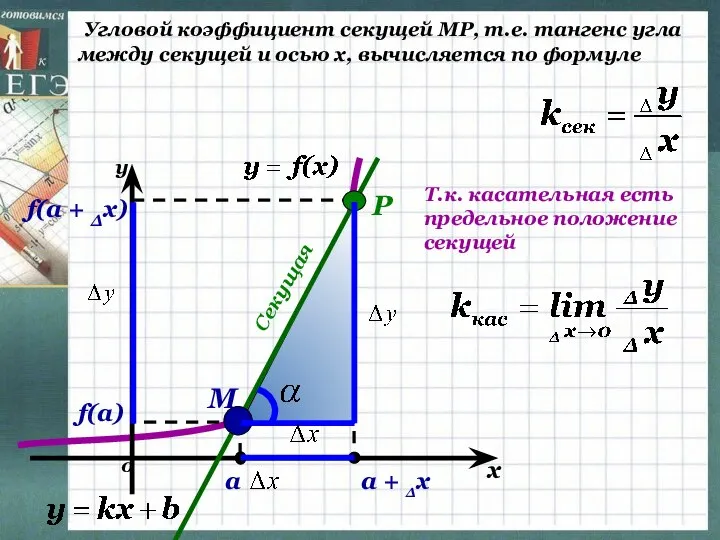
Угловой коэффициент секущей МР, т.е. тангенс угла между секущей и осью х, вычисляется по формуле
Секущая
а
f(a)
М
Р
f(a + ∆x)
а + ∆x
Т.к. касательная есть предельное положение секущей

Итак, две различные задачи привели к
одной и той же математической модели –
пределу отношения приращения функции к
приращению аргумента при условии, что
приращение аргумента стремится к нулю
Многие задачи физики, химии, экономики
и т.д. приводят в процессе решения к такой
же модели. Значит, эту математическую
модель надо специально изучить, т.е.
присвоить ей новый термин;
ввести для нее обозначение;
исследовать свойства новой модели

Пусть функция у =f(x) определена в точке х и в некоторой ее окрестности. Дадим аргументу х приращение ∆x, такое, чтобы не выйти из указанной окрестности. Найдем соответствующее приращение функции ∆у и составим отношение .
или

Если f(x) имеет производную в точке х, то эта функция называется дифференцируемой в этой точке
Если f(x) имеет производную в каждой точке промежутка, то говорят, что эта функция имеет производную на этом промежутке
Операция нахождения производной называется дифференцированием

Дано: S(t) = 2t2
Найти : мгновенную скорость
Пример №1
Пример №2
Найти производную функции
f(x)= х2
Пример №3
Найти производную функции
f(x)= х3
(х2)‘=2х
(х3)‘=3х2

Примеры №4 и №5 стр. 227

Первые формулы!
(х2)‘=2х
(х3)‘=3х2
с‘=0
(кх+в)‘=к