располагаются в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.
Тетраэдры в технике
Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов и т. д. Стержни испытывают только продольные нагрузки.
Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
Граф четверичного триггера представляет собой тетраэдр.







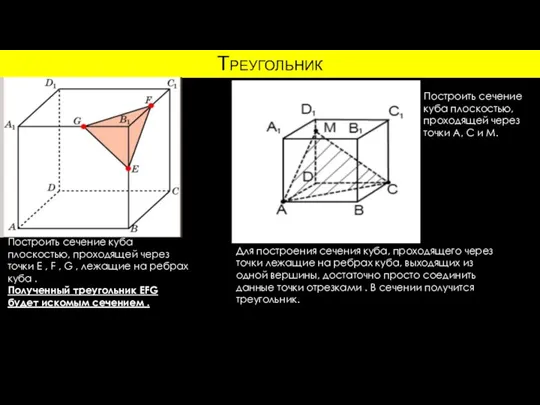
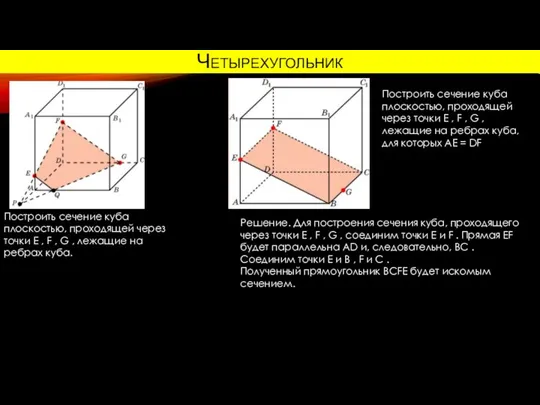
 Сокращение дробей. Самоанализ
Сокращение дробей. Самоанализ Геометрический конструктор GeoGebra
Геометрический конструктор GeoGebra Кусочная функция
Кусочная функция Презентация на тему Число 0 Цифра 0
Презентация на тему Число 0 Цифра 0  Повторение по математике
Повторение по математике 9fc9887af90115bf
9fc9887af90115bf Урок математики 20.09
Урок математики 20.09 Презентация на тему Повторяем таблицу умножения
Презентация на тему Повторяем таблицу умножения  Степенная функция
Степенная функция Нечеткие числа
Нечеткие числа Теорема Пифагора
Теорема Пифагора Дифференциальные уравнения и их применение в медицинской практике. Элементы комбинаторики. Случайные величины
Дифференциальные уравнения и их применение в медицинской практике. Элементы комбинаторики. Случайные величины Процент
Процент Презентация на тему НЕРАВЕНСТВО ТРЕУГОЛЬНИКА
Презентация на тему НЕРАВЕНСТВО ТРЕУГОЛЬНИКА  Теорема Виета. Устная работа
Теорема Виета. Устная работа Циркуль. Учимся работать циркулем (2 класс, технология)
Циркуль. Учимся работать циркулем (2 класс, технология) Решение текстовых задач. 5 класс
Решение текстовых задач. 5 класс Литр. Задачи
Литр. Задачи Презентация на тему КВН по информатике и математике
Презентация на тему КВН по информатике и математике  Описанная окружность треугольника
Описанная окружность треугольника Презентация на тему Аксиома параллельных прямых
Презентация на тему Аксиома параллельных прямых  Правильные многогранники в природе
Правильные многогранники в природе Деление одночлена на одночлен
Деление одночлена на одночлен Математический КВН. Счет и вычисления
Математический КВН. Счет и вычисления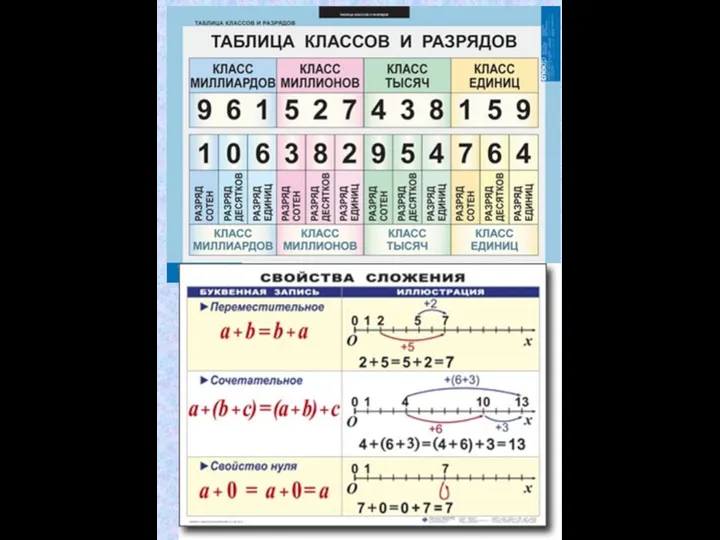 Таблица классов и разрядов. Свойства сложения
Таблица классов и разрядов. Свойства сложения Спасение похищенных чисел. Урок-сказка
Спасение похищенных чисел. Урок-сказка Формулы сокращенного умножения. Интерактивный плакат
Формулы сокращенного умножения. Интерактивный плакат Произведение многочленов
Произведение многочленов