Слайд 2Решение различных экономических задач в формате ЕГЭ часто сводится к отысканию экстремальных

(минимальных или максимальных) значений некоторой функции. Нередко такими функциями являются линейная функция или квадратичная функция
Слайд 3Линейная функция y=kx+m
1) Если задан промежуток, которому принадлежит х, то экстремальное значение

функция принимает на одном из концов промежутка.
Слайд 4Линейная функция y=kx+m
2) Если линейная функция рассматривается только на множестве целых чисел,

то число из этого промежутка, при котором функция принимает наибольшее или наименьшее значение, будет ближайшим целым числом к тому концу промежутка, на котором она принимает соответствующее экстремальное значение
Слайд 5Квадратичная функция
Квадратичная функция принимает экстремальное значение при

Слайд 6№1.
Индивидуальный предприниматель за 288 тысяч рублей приобрёл цех по производству носков. Затраты

на изготовление х тысяч пар носков в месяц составляют (x²+6x+7) тысяч рублей. Если продавать одну пару носков по с рублей, то прибыль от продажи х тысяч пар носков в месяц составит сх - (x²+6x+7) тысяч рублей (с>6). Предприниматель имеет возможность изготавливать и продавать такое количество пар носков, которое обеспечивает наибольшую прибыль. При каком наименьшем значении с предприниматель окупит затраты на покупку цеха не более чем за 32 месяца?
Слайд 9№2
Крупный бизнесмен является владельцем двух заводов, выпускающих одинаковую продукцию. На втором заводе

используется более современное оборудование, позволяющее за одинаковое время с первым заводом производить больше продукции, чем на первом заводе. Известно, что если рабочие первого завода трудятся суммарно t² часов в неделю, то за это время они производят 2t единиц товара. А если рабочие второго завода трудятся суммарно t² часов в неделю, то за это время они производят 5t единиц товара. За обоих заводах за 1 час работы рабочему платят 500 рублей. Какое наибольшее число единиц продукции можно будет выпустить на обоих заводах при условии, что заработную плату на предстоящую неделю можно будет выплатить в размере 1 450 000 рублей?
Слайд 12Задание для самостоятельной работы
1) Затраты на строительство нового аквапарка составляют 50 млн

рублей. Стоимость обслуживания х тысяч посетителей за сезон равна 0,25х²+4х+6 млн рублей. Если за обслуживание одного посетителя за сезон брать с тысяч рублей (с>4), то прибыль за обслуживание х тысяч посетителей за сезон будет равна сх-(0,25х²+4х+6) млн рублей. По окончанию строительства у руководства аквапарка будет возможность организовать обслуживание такого числа посетителей, которое обеспечивает максимальную прибыль. При каком наименьшем значении с окупятся затраты на строительство аквапарка не более чем за 5 сезонов?











 Повторим… Уравнение линии на плоскости
Повторим… Уравнение линии на плоскости Как построить графики функций y = f(x) + b и y = f(x + a), если известен график функции y = f(x)
Как построить графики функций y = f(x) + b и y = f(x + a), если известен график функции y = f(x) Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной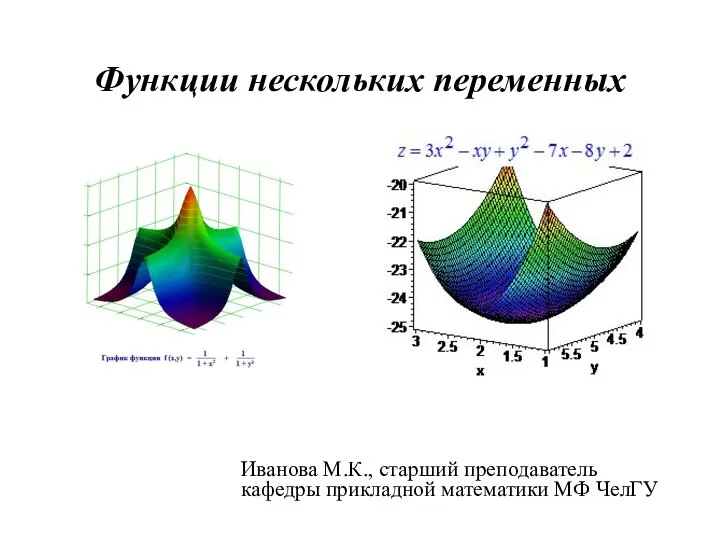 Функции нескольких переменных
Функции нескольких переменных Вписанi й описанi. Чотирикутники
Вписанi й описанi. Чотирикутники Открой свою звезду. Математический диктант
Открой свою звезду. Математический диктант Прямая на плоскости
Прямая на плоскости Обыкновенные дроби (с использованием контрольно-измерительных материалов)
Обыкновенные дроби (с использованием контрольно-измерительных материалов) Комбінаторика, як розділ математики. Сполуки без повторень. Найпростіші комбінаторні задачі
Комбінаторика, як розділ математики. Сполуки без повторень. Найпростіші комбінаторні задачі Исторические задачи по математике
Исторические задачи по математике ТАиФЯ № 1 (Введение)
ТАиФЯ № 1 (Введение) Теорема Байеса
Теорема Байеса Теория Графов
Теория Графов Решение задач с помощью теоремы Пифагора
Решение задач с помощью теоремы Пифагора Свойства степени с рациональным показателем
Свойства степени с рациональным показателем Б. Кавальери и его метод неделимых
Б. Кавальери и его метод неделимых Тригонометрические уравнения. Устный счет
Тригонометрические уравнения. Устный счет Числовое значение буквенного выражения (часть 2)
Числовое значение буквенного выражения (часть 2) Площадь поверхности цилиндра
Площадь поверхности цилиндра Дифференциальные уравнения
Дифференциальные уравнения Роль математики в медицине
Роль математики в медицине Математика в экскурсиях
Математика в экскурсиях Экономический факторный анализ. Теорема о среднем
Экономический факторный анализ. Теорема о среднем Основное свойство дроби
Основное свойство дроби Математика «Сравнение трехзначных чисел» 3 класс ОС «Школа 2100» Загатина А.О.
Математика «Сравнение трехзначных чисел» 3 класс ОС «Школа 2100» Загатина А.О. График функции y = ax^2 + n
График функции y = ax^2 + n Методы решения творческих задач
Методы решения творческих задач Состав чисел в пределах 10. Урок №80
Состав чисел в пределах 10. Урок №80