Классическая формула подсчета результатов

Пример: выпадение герба и решки образуют полную группу событий.
Группа событий называется
полной, если при проведении
опыта всегда происходит
одно из этих событий.

Случаем называются равновозможные
попарно несовместные события,
образующие полную группу.
Случай называется благоприятным
некоторому событию, если
наступление этого случая
влечет за собой наступление
данного события.

При бросании игральной кости возможно 6 случаев, из которых три случая будут благоприятны событию А - появлению четного числа очков.
Пример.

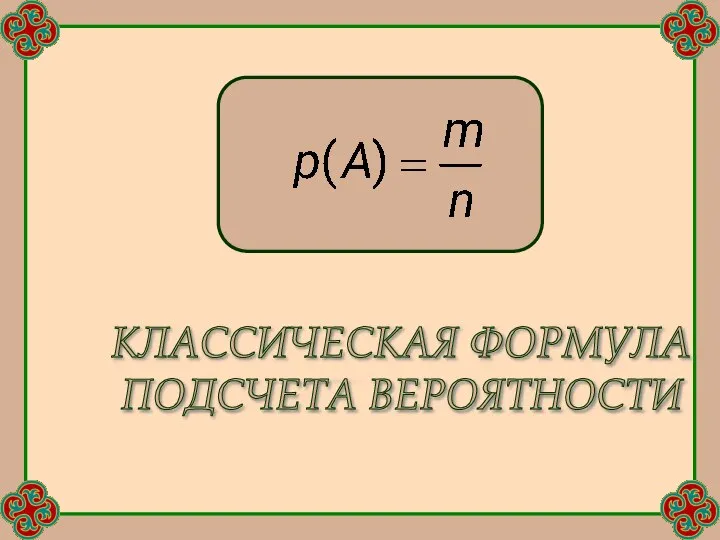
Вероятность события можно оценить по относительной доле благоприятных случаев.
Если n - общее число случаев, а m - число случаев, благоприятных событию А, то вероятность события А может быть найдена по формуле:

КЛАССИЧЕСКАЯ ФОРМУЛА ПОДСЧЕТА ВЕРОЯТНОСТИ

В качестве единицы измерения вероятности принимается вероятность достоверного события. Т.е. вероятность события, которое всегда происходит, полагается равной 1.
Вероятные но недостоверные события будут иметь вероятность меньше 1.
Вероятность невозможного события полагается равной 0.
Таким образом, вероятность любого события находится в интервале от 0 до 1.

Классическая формула для вероятности справедлива только в том случае, если все исходы опыта можно разделить на группы равновозможных случаев. Часто это является следствием симметрии, которой обладает опыт.

Пример.
Брошены два игральных кубика.
Найти вероятность событий: А-
сумма выпавших очков – четная,
В – произведение очков больше 20.

Всего будет 36 событий, которые являются случаями, поскольку они равновозможны и образуют полную группу, т.е. n=36.
Решение.
Событию А будет благоприятно 18 случаев, т.е. m=18.