Взаимное расположение прямых в пространстве. Угол между двумя прямыми

Как известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку).

В пространстве мы можем представить ситуацию, когда две прямые не пересекаются, но они и не параллельны.

Определение:
Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Теорема "Признак скрещивающихся прямых"
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).

В пространстве прямые расположены следующим образом:
1. Параллельны

В пространстве прямые расположены следующим образом:
2. Пересекающиеся

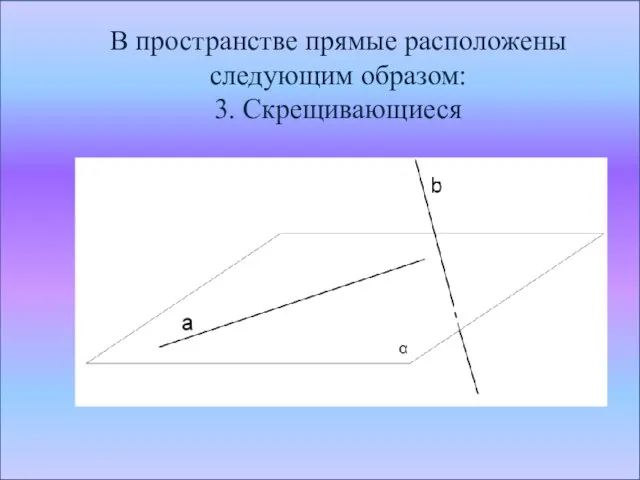
В пространстве прямые расположены следующим образом:
3. Скрещивающиеся

Теорема
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

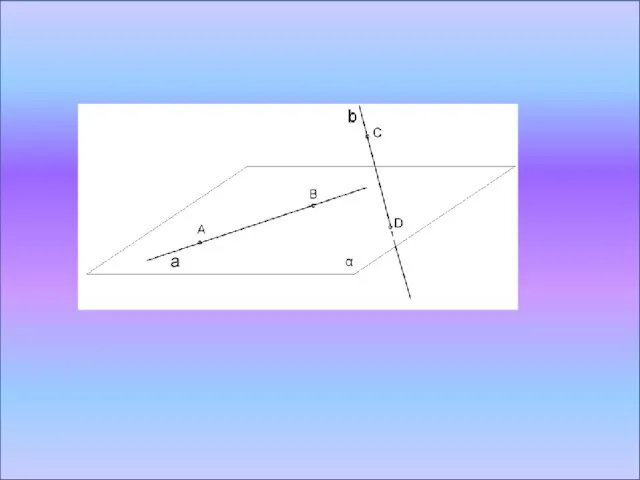
Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.
1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.

Углы между прямыми

Обрати внимание!!!
Провести соответственные параллельные прямые данным скрещивающимися прямым можно через любую точку.
Иногда удобно выбрать эту точку на одной из данных скрещивающихся прямых и провести через эту точку прямую параллельную другой из скрещивающихся прямых.

Задача №1
Дан куб ABCDA1B1C1D1

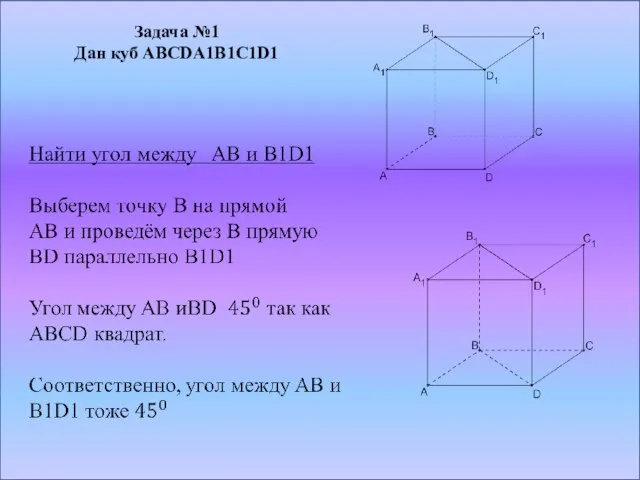
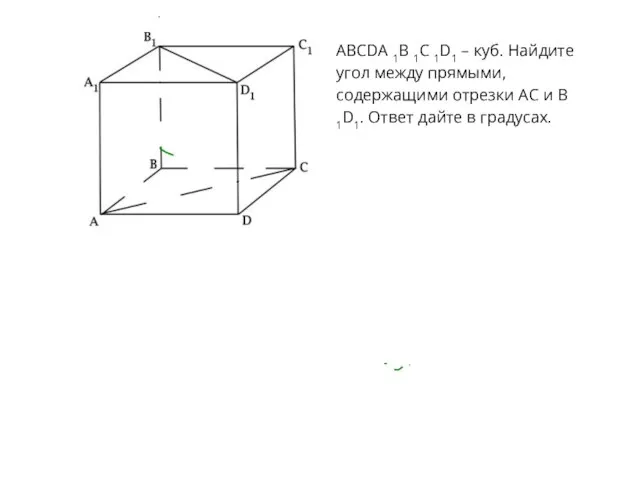
ABCDA 1B 1C 1D1 – куб. Найдите угол между прямыми, содержащими отрезки AC и B 1D1. Ответ дайте в градусах.

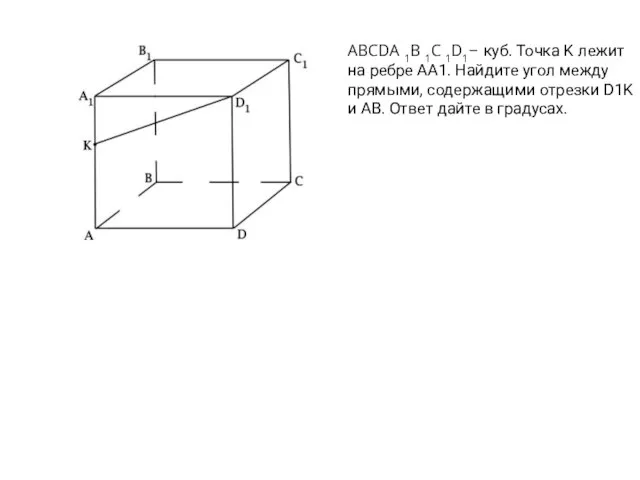
ABCDA 1B 1C 1D1– куб. Точка K лежит на ребре AA1. Найдите угол между прямыми, содержащими отрезки D1K и AB. Ответ дайте в градусах.