Содержание
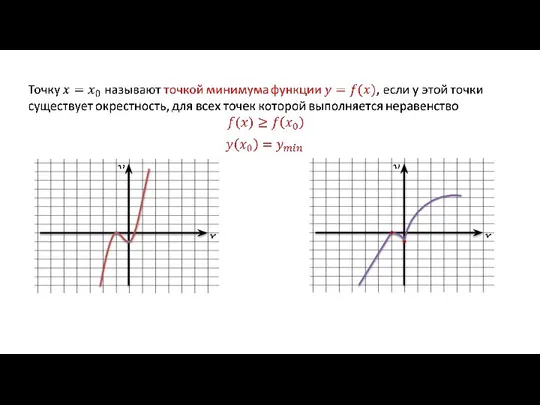
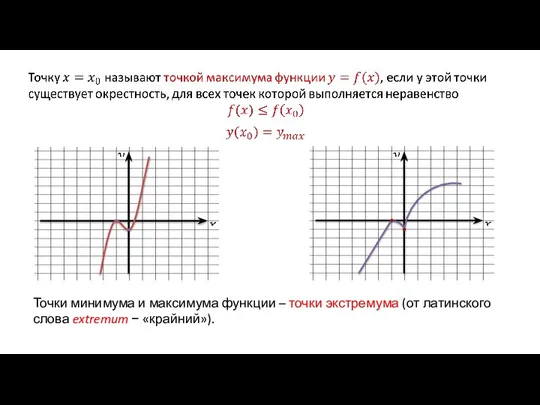
- 4. Точки минимума и максимума функции – точки экстремума (от латинского слова extremum − «крайний»).
- 5. Пьер Ферма (1601 – 1665 гг.) Леонард Эйлер (1707 – 1783 гг.) Колин Маклорен (1698 –
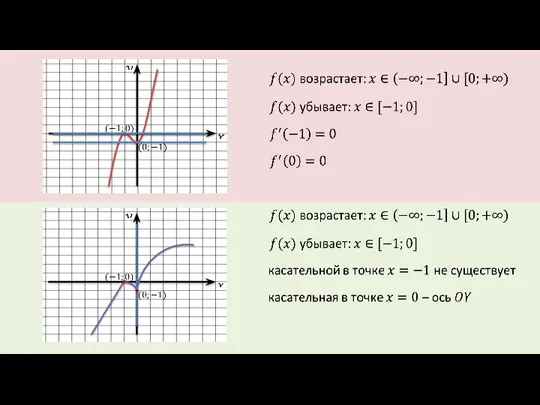
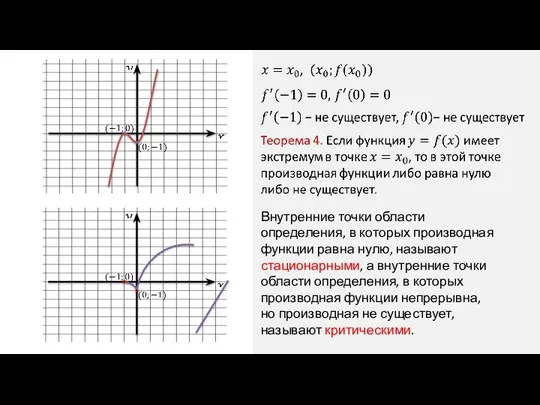
- 6. Внутренние точки области определения, в которых производная функции равна нулю, называют стационарными, а внутренние точки области
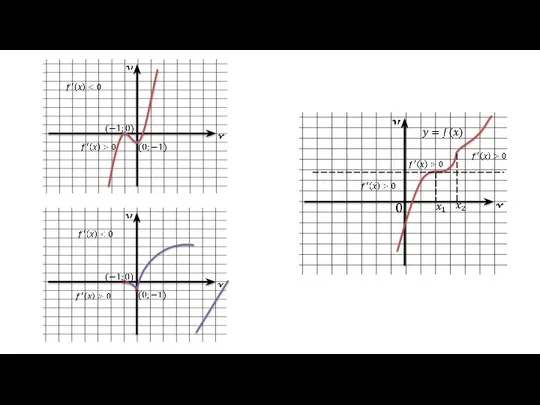
- 9. Пример:
- 11. Пример:
- 13. Скачать презентацию





 Обозначение числа буквой и выражением
Обозначение числа буквой и выражением Обобщающее повторение. Алгебра 11 класс
Обобщающее повторение. Алгебра 11 класс Формулы половинного аргумента
Формулы половинного аргумента Деление с остатком
Деление с остатком Координаты вектора
Координаты вектора Подготовка к контрольной работе. Уравнения
Подготовка к контрольной работе. Уравнения Преобразование буквенных выражений
Преобразование буквенных выражений Знакомство с образованием чисел второго десятка
Знакомство с образованием чисел второго десятка Правильные многоугольники
Правильные многоугольники Застосування кількох способів розкладання многочленів на множники
Застосування кількох способів розкладання многочленів на множники Статистическая сводка и группировка. Лекция 3
Статистическая сводка и группировка. Лекция 3 Дифференциальные уравнения
Дифференциальные уравнения Алгоритм письмового додавання, якщо сума розрядних одиниць дорівнює 10
Алгоритм письмового додавання, якщо сума розрядних одиниць дорівнює 10 Дифференциальные исчисления функции одной независимой переменной
Дифференциальные исчисления функции одной независимой переменной Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе
Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе Презентация на тему ФАКТОРИАЛ
Презентация на тему ФАКТОРИАЛ  Функция и способы ее задания. Преобразования графиков функций
Функция и способы ее задания. Преобразования графиков функций Коррекция СУ
Коррекция СУ Презентация на тему Плоскость. Прямая. Луч
Презентация на тему Плоскость. Прямая. Луч  Сравнение многозначных чисел. 4 класс
Сравнение многозначных чисел. 4 класс Linear Algebra. Lecture 2
Linear Algebra. Lecture 2 Признак параллельности прямых по равенству соответственных углов
Признак параллельности прямых по равенству соответственных углов Перпендикулярные прямые, перпендикулярные к плоскости
Перпендикулярные прямые, перпендикулярные к плоскости Треугольники. Часть II. ЕГЭ
Треугольники. Часть II. ЕГЭ Наряди елочку. Устный счёт
Наряди елочку. Устный счёт Урок 9 Розв. типових задач
Урок 9 Розв. типових задач Интегральное исчисление
Интегральное исчисление ВПР вариант 16 № 11. Решение трудной задачи
ВПР вариант 16 № 11. Решение трудной задачи