Содержание
- 2. План построения графика функции с помощью производной Найти область определения функции и определить точки разрыва если
- 3. Как найти промежутки выпуклости, вогнутости и точку перегиба графика функции Промежутки выпуклости и вогнутости кривой можно
- 4. Для нахождения интервалов выпуклости графика функции используют следующий алгоритм: Находят f΄(х), а затем f ΄΄(х) Находят
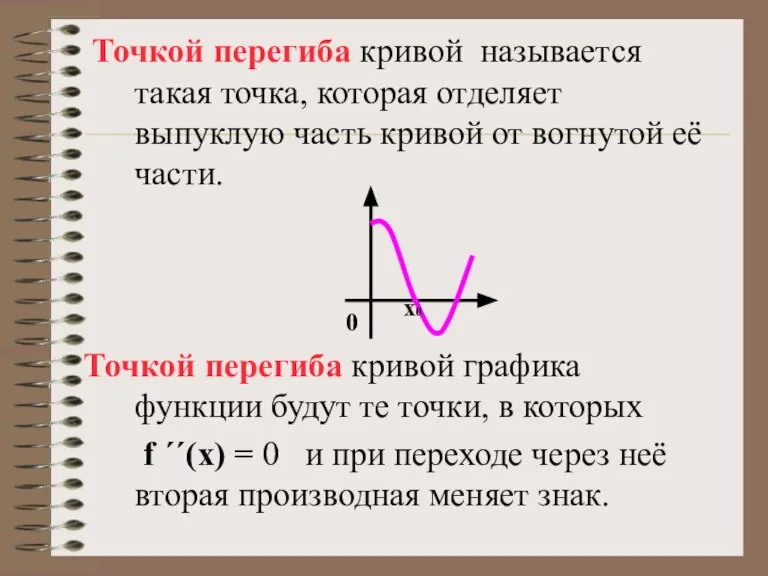
- 5. Точкой перегиба кривой называется такая точка, которая отделяет выпуклую часть кривой от вогнутой её части. Точкой
- 6. Найти интервалы выпуклости и точку перегиба функции Решение. Найдем у΄(х) и у΄΄(х): у΄(х) = 4х³-12х =>
- 7. Например: исследовать функцию у = 2х³+3х² -1 и построить её график Решение. D(у)= (-∞; +∞), четность
- 8. Найдем промежутки монотонности: при x ϵ (-∞; -1] и [0; + ∞) - функция возрастает при
- 9. Найдем ещё некоторые точки (контрольные, дополнительные): т.к. х=-1 – точка максимума, то уmax=0 => (-1; 0)
- 10. Составим таблицу: Найдем f ΄΄(х). f΄΄(х) =(6х(х+1))΄=12х+6 = 6(2х+1) f΄΄(х)=0 => 6(2х+1)=0 => х = -0,5
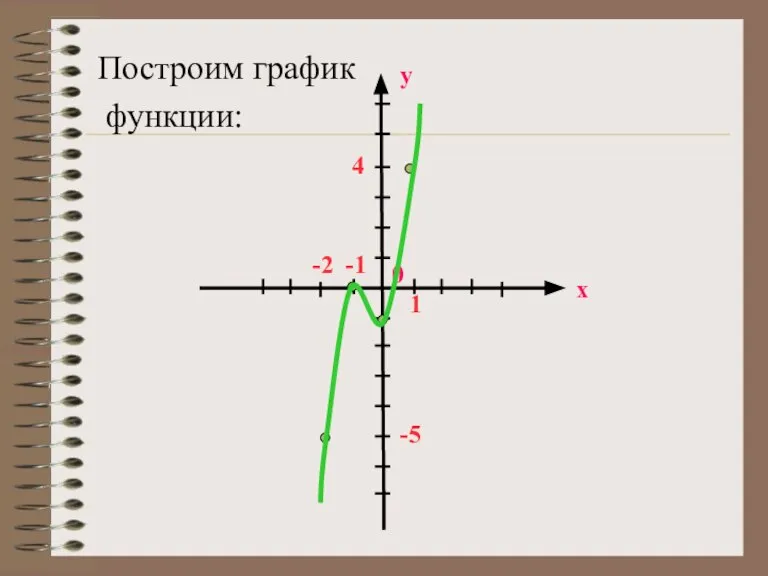
- 11. Построим график функции: х у 0 -1 -2 4 1 -5
- 12. Исследовать функцию и построить её график 1) у = 3х² - х³ 2) у = -
- 13. Работа с графиками функций
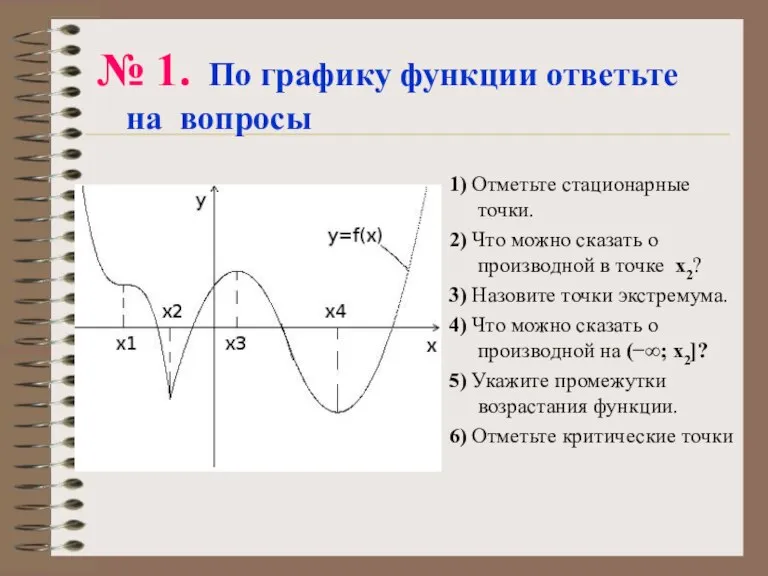
- 14. № 1. По графику функции ответьте на вопросы 1) Отметьте стационарные точки. 2) Что можно сказать
- 15. Проверим ответы 1. х1,х3,х4 2. не существует 3. х2,х3,х4 4. f′(х) ≤ 0 5. [х2; х3]U
- 16. № 2. Постройте график непрерывной функции у = f(х), определенной на [а;в], удовлетворяющей следующим условиям: а)
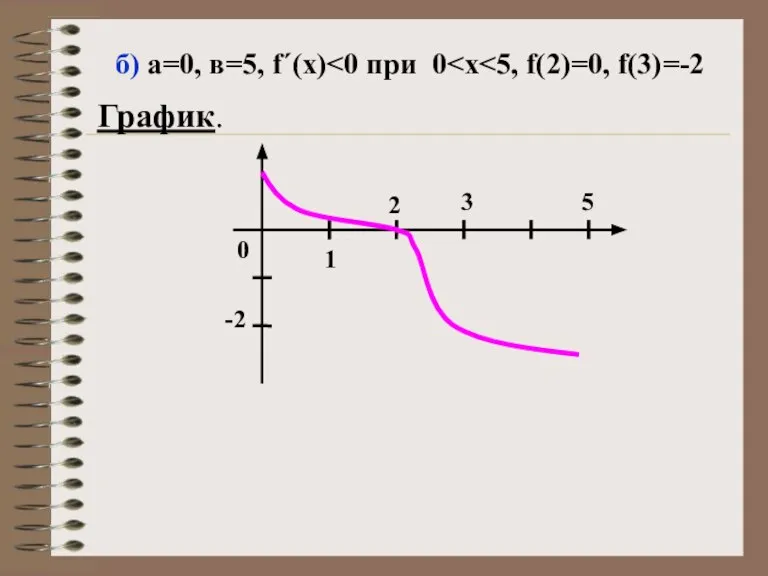
- 17. б) а=0, в=5, f΄(х) График. 0 -2 3 5 2 1
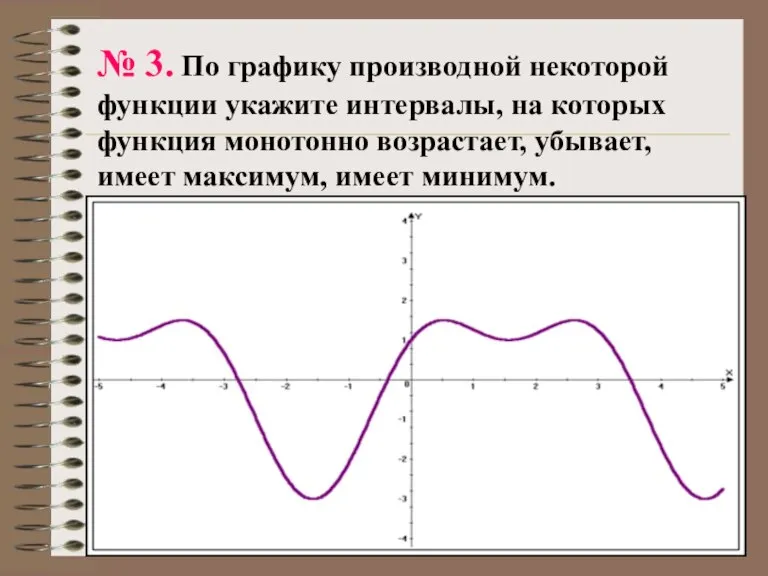
- 18. № 3. По графику производной некоторой функции укажите интервалы, на которых функция монотонно возрастает, убывает, имеет
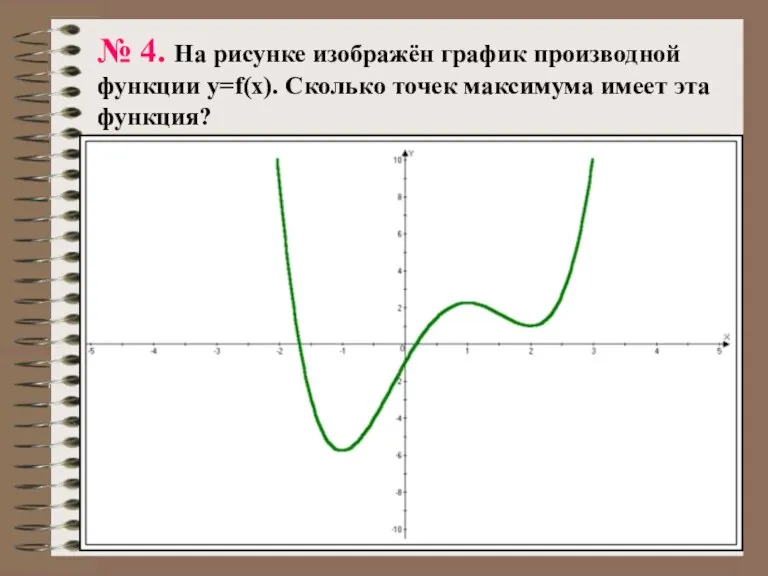
- 19. № 4. На рисунке изображён график производной функции y=f(x). Сколько точек максимума имеет эта функция?
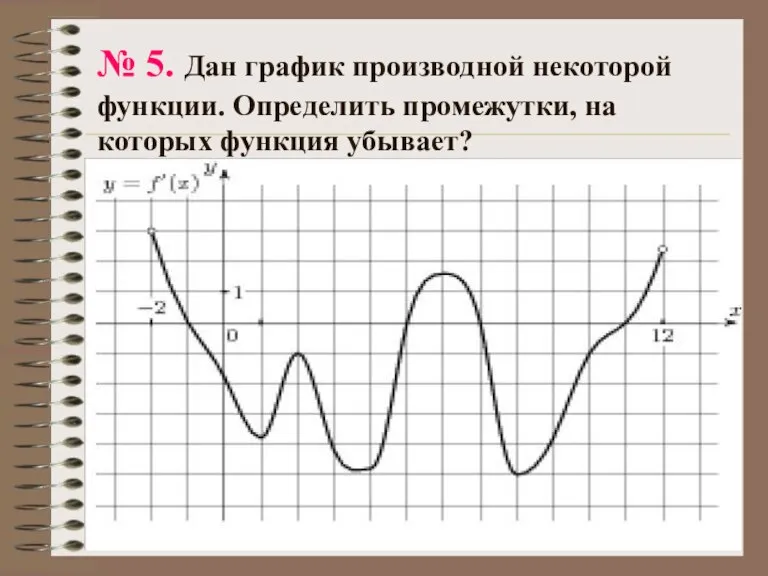
- 20. № 5. Дан график производной некоторой функции. Определить промежутки, на которых функция убывает?
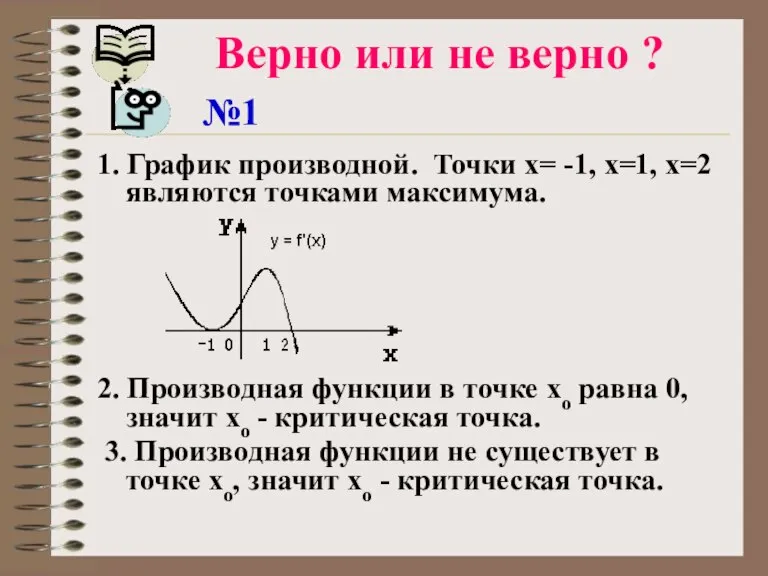
- 21. Верно или не верно ? №1 1. График производной. Точки х= -1, х=1, х=2 являются точками
- 22. 4. Критическая точка является точкой экстремума. 5. Точка экстремума является критической точкой. 6. Функция y(x) непрерывна
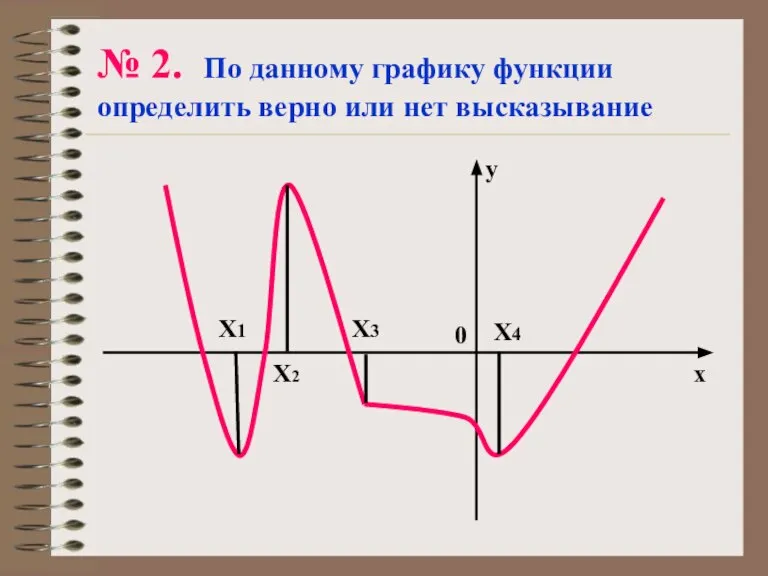
- 23. № 2. По данному графику функции определить верно или нет высказывание 0 х у Х1 Х2
- 24. Точка х1 – точка минимума. Точка х1 – точка перегиба. В точках х2 и х4 касательная
- 26. Скачать презентацию





![Найдем промежутки монотонности: при x ϵ (-∞; -1] и [0; + ∞)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1149034/slide-7.jpg)




![№ 2. Постройте график непрерывной функции у = f(х), определенной на [а;в],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1149034/slide-15.jpg)


 Геро́н Александри́йский
Геро́н Александри́йский Линейные пространства
Линейные пространства Элементы теории вероятностей
Элементы теории вероятностей 15 задание. Виды. Делимость. Числовая последовательность. Конъюнкция. Множества
15 задание. Виды. Делимость. Числовая последовательность. Конъюнкция. Множества Дифференциальные уравнения
Дифференциальные уравнения Площадь. Площадь прямоугольника
Площадь. Площадь прямоугольника Детерминационный, факторный и кластерный анализ
Детерминационный, факторный и кластерный анализ mypresentation.ru
mypresentation.ru Геометрический биатлон
Геометрический биатлон Задачи на готовых чертежах. Ромб
Задачи на готовых чертежах. Ромб Презентация на тему Внетабличное умножение и деление
Презентация на тему Внетабличное умножение и деление  Упражнения
Упражнения Доли. Зарядка для ума
Доли. Зарядка для ума Решение задач. Урок 22
Решение задач. Урок 22 Системы уравнений
Системы уравнений Презентация на тему Преобразование плоскости
Презентация на тему Преобразование плоскости  Построить линейный угол двугранного угла
Построить линейный угол двугранного угла Задачи на построение
Задачи на построение Задачи на составление уравнений. 7 класс
Задачи на составление уравнений. 7 класс Повторение и закрепление. Итоговое повторение за год. 4 класс
Повторение и закрепление. Итоговое повторение за год. 4 класс Второй и третий признаки равенства треугольников. LOGO
Второй и третий признаки равенства треугольников. LOGO Путешествуем с теоремой Пифагора. 8 класс
Путешествуем с теоремой Пифагора. 8 класс Διδακτική Ενότητα Α: Συνδυαστική Ανάλυση
Διδακτική Ενότητα Α: Συνδυαστική Ανάλυση Презентация на тему Умножение числа 2
Презентация на тему Умножение числа 2  Алгоритм упаковки прямоугольников
Алгоритм упаковки прямоугольников Итоговая контрольная работа
Итоговая контрольная работа Презентация на тему Ознакомление с различными способами деления суммы на число
Презентация на тему Ознакомление с различными способами деления суммы на число  Статистическая сводка и группировка
Статистическая сводка и группировка