Слайд 2Сечение куба плоскостью.
Задача1: Построить сечение куба плоскостью, которая проходит через точки K,

L, M, расположенные на его ребрах.
Слайд 3Дано:
ABCDА1B1C1D1 -куб,
точка К принадлежит ребру A1В1, точка L принадлежит
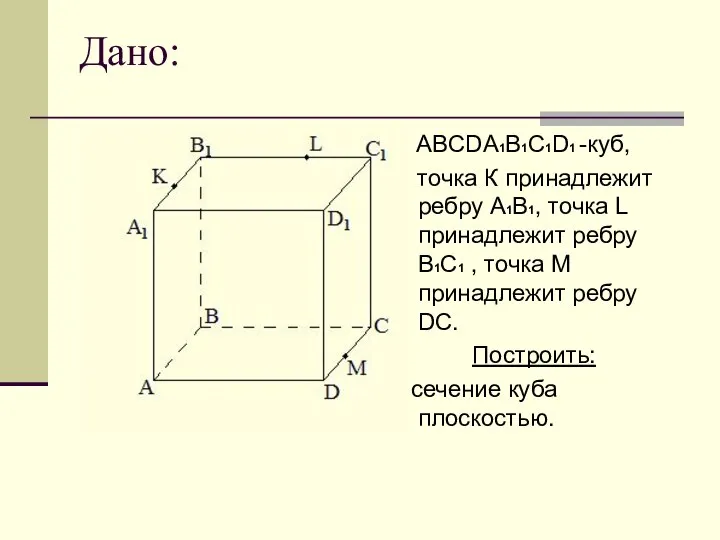
ребру В1C1 , точка М принадлежит ребру DC.
Построить:
сечение куба плоскостью.
Слайд 4Решение:
Проведем прямую КL и отметим точки ее пересечения с продолжениями соответствующих
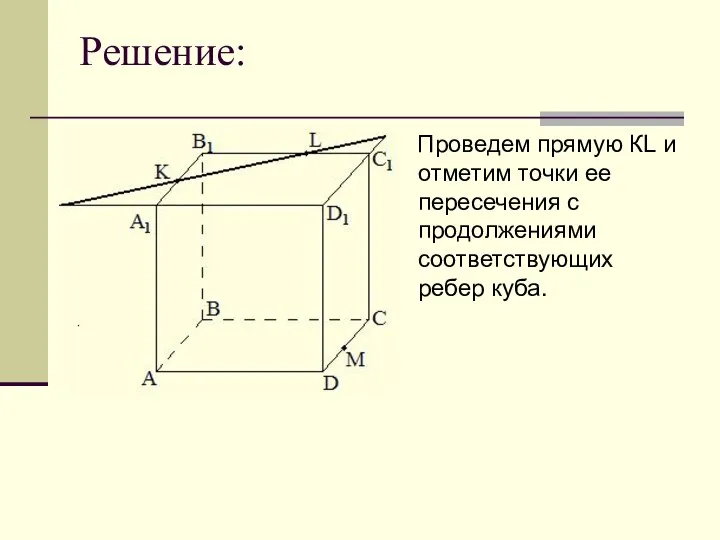
ребер куба.
Слайд 5 Получим еще две точки, лежащие в плоскости сечения и на продолжениях
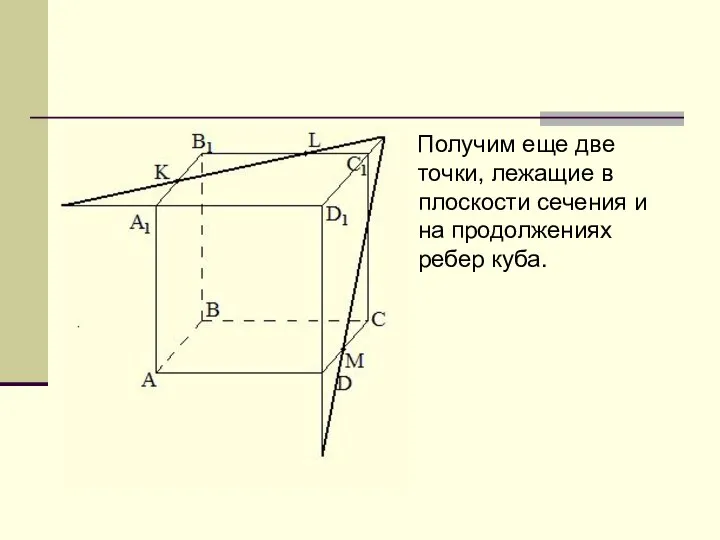
ребер куба.
Слайд 6 Проводя аналогичным образом прямые в плоскостях других граней куба мы построим
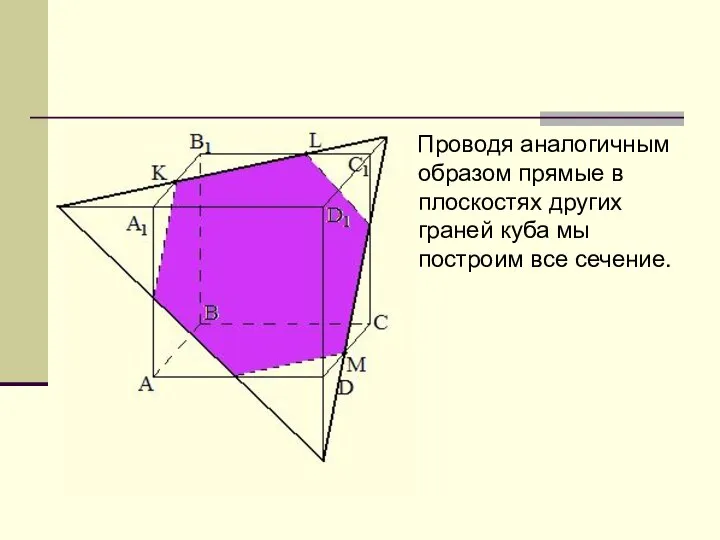
все сечение.
Слайд 7Сечение пирамиды плоскостью.
Задача 2: Постройте сечение пирамиды ABCD плоскостью проходящей через точки

K, L, M.
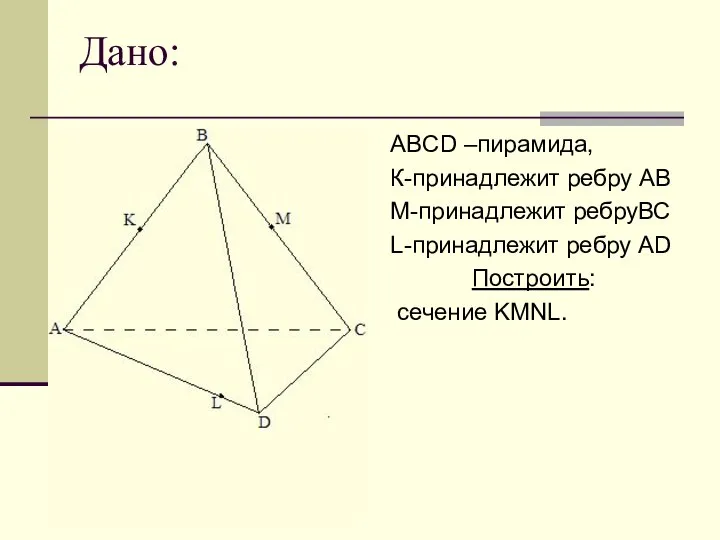
Слайд 8Дано:
ABCD –пирамида,
К-принадлежит ребру АВ
М-принадлежит ребруВС
L-принадлежит ребру AD
Построить:
сечение KMNL.
Слайд 9Решение:
Провести в плоскости ABD прямую KL (используя метод следов – прямые, по
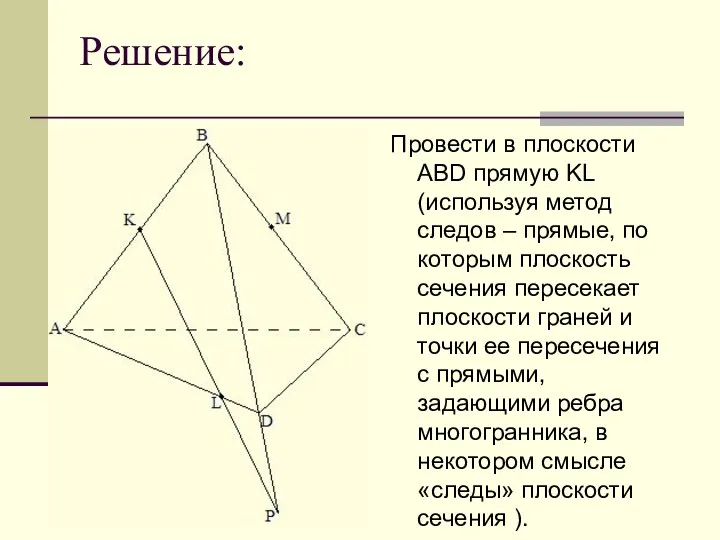
которым плоскость сечения пересекает плоскости граней и точки ее пересечения с прямыми, задающими ребра многогранника, в некотором смысле «следы» плоскости сечения ).
Слайд 10Обозначим через Р точку пересечения KL и BD.
Проводим прямую РМ, получаем точку
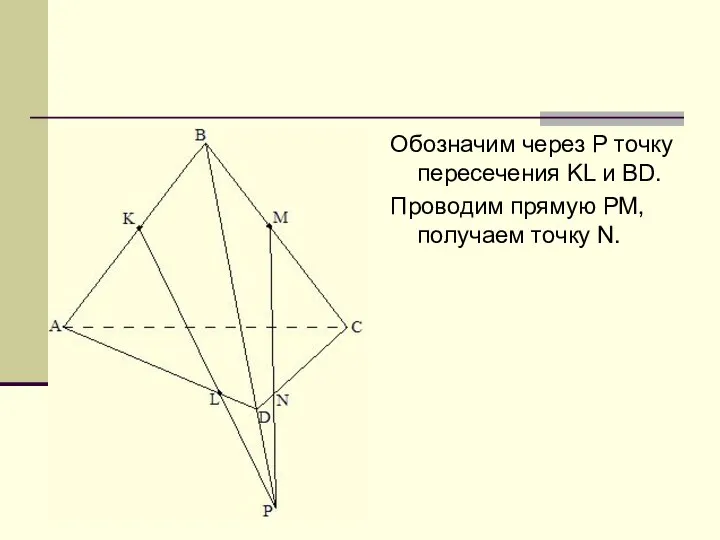
N.
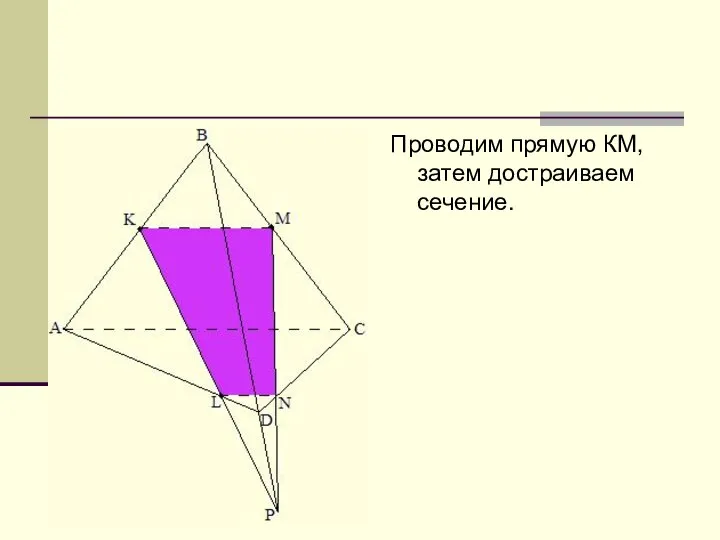
Слайд 11Проводим прямую КМ, затем достраиваем сечение.
Слайд 12Задание 1:
На ребрах взяты точки K, L и M, как показано
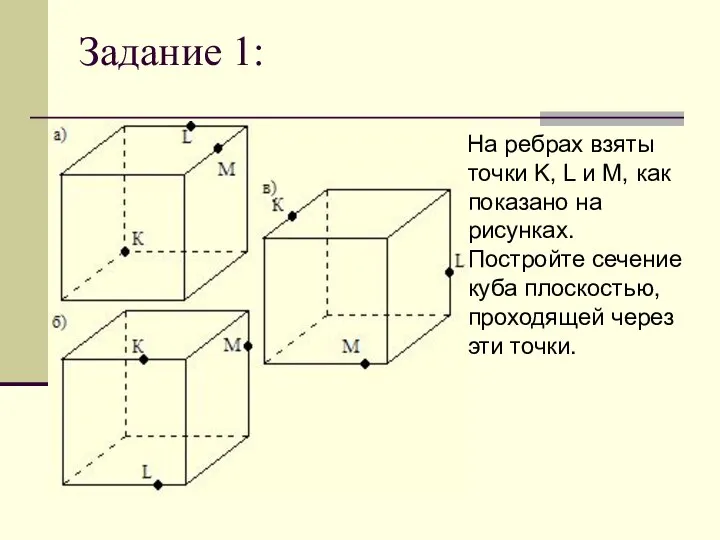
на рисунках. Постройте сечение куба плоскостью, проходящей через эти точки.











 Признаки параллелограмма. 8 класс
Признаки параллелограмма. 8 класс Неопределённый и определённый интеграл
Неопределённый и определённый интеграл Веселый паровоз. Мультимедийное пособие по математике
Веселый паровоз. Мультимедийное пособие по математике Проект Колодец. Деловая игра по теме Цилиндр
Проект Колодец. Деловая игра по теме Цилиндр Презентация на тему Деление многозначных чисел
Презентация на тему Деление многозначных чисел  Алгоритм вычислений
Алгоритм вычислений Логика
Логика Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8
Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8 Параллелограмм и трапеция. Урок 6
Параллелограмм и трапеция. Урок 6 Пирамида. Виды пирамид
Пирамида. Виды пирамид Игра-тренажёр Округление чисел
Игра-тренажёр Округление чисел Вычисление одномерных, двумерных и интегралов c переменным верхним пределом
Вычисление одномерных, двумерных и интегралов c переменным верхним пределом Алгебра 10кл - Презентация к уроку 1 (Самойлова Г. А.)
Алгебра 10кл - Презентация к уроку 1 (Самойлова Г. А.) Правильные многогранники
Правильные многогранники Алгебраические выражения
Алгебраические выражения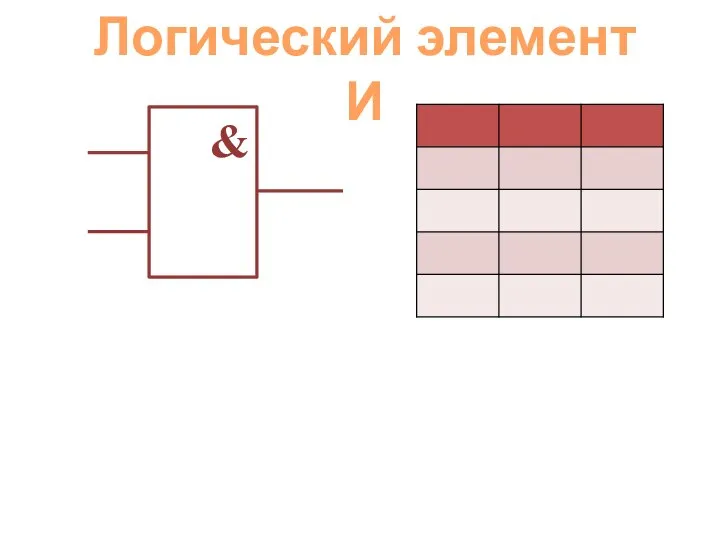 Логический элемент
Логический элемент Презентация на тему Вектор
Презентация на тему Вектор  Правила с двумя решениями. Подход Неймана – Пирсона
Правила с двумя решениями. Подход Неймана – Пирсона Координатный метод в решении задач на плоскости Белобородова Н. Е., учитель математики МАОУ «СОШ №2»
Координатный метод в решении задач на плоскости Белобородова Н. Е., учитель математики МАОУ «СОШ №2» Презентация на тему Отрезок. Графики
Презентация на тему Отрезок. Графики  Стереометрия 1. ЕГЭ
Стереометрия 1. ЕГЭ Окружность. 5 класс
Окружность. 5 класс Урок 14. Первый признак равенства треугольников
Урок 14. Первый признак равенства треугольников Сложение и вычитание вида ± 1, ± 2, ± 3 (1 класс)
Сложение и вычитание вида ± 1, ± 2, ± 3 (1 класс) Презентация на тему Римские цифры (3 класс)
Презентация на тему Римские цифры (3 класс)  Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Тестирование генераторов случайных чисел
Тестирование генераторов случайных чисел Презентация на тему Подготовка к ГИА 2013
Презентация на тему Подготовка к ГИА 2013