Группировки в историческом исследовании

Группировка является методом исследования содержания изучаемого явления. На ее основе рассчитываются обобщающие показатели по группам, выявляется строение совокупности, взаимосвязи между изучаемыми признаками, а затем проводится анализ полученных результатов.

Группировка - это распределение множества единиц исследуемой совокупности по группам в соответствии с существенным для данной группы признаком. Метод группировки позволяет обеспечивать первичное обобщение данных, представление их в более упорядоченном виде.

Благодаря группировке можно соотнести сводные показатели по совокупности в целом со сводными показателями по группам. Появляется возможность сравнивать, анализировать причины различий между группами, изучать взаимосвязи между признаками.

Группировка позволяет делать вывод о структуре совокупности и о роли отдельных групп этой совокупности. Именно группировка формирует основу для последующей сводки и анализа данных.

Основными категориями метода группировок являются группировочный признак (основание группировки) и интервал.
Группировочным признаком (основанием группировки) называется признак, по которому происходит выделение однородных групп.

Правильный выбор существенного группировочного признака дает возможность сделать научно обоснованные выводы по результатам статистического исследования. Группировочные признаки могут иметь как количественное выражение (объем, доход, курс валюты, возраст и т.д.), так и качественное (форма собственности предприятия, пол человека, отраслевая принадлежность, семейное положение и т.д.).

В качестве группировочного обычно выбирается один из существенных легко распознаваемых признаков, носящих как атрибутивный, так и количественный характер.

При определении числа групп, как правило, учитываются задача исследования, объем совокупности и виды признаков, которые берутся в качестве основания группировки. Например, по количественному признаку возраст населения может быть разбит на самые различные группы. Их число будет зависеть от поставленных задач. Например, это могут быть группы по возрасту трудоспособного населения; экономически активного населения и т.д.

Если берется, предположим, такой качественный признак, как образование, то групп будет ровно столько, сколько существует ступеней или профилей образования. В образовании по ступеням групп будет шесть (неполное среднее; среднее; неполное среднее специальное; специальное среднее; неполное высшее; высшее).

По профилю образования количество групп может совпадать или с числом профессиональных групп, или с числом сфер образования (гуманитарное; инженерно-техническое; естественнонаучное).

Интервал – это совокупность варьирующих значений признака в группе, он определяет количественные границы групп, а его ширина представляет собой промежуток между максимальным и минимальным значениями признака в группе.

При выполнении группировок используются следующие типы интервалов:
• равные – во всех выделенных группах ширина интервала является одинаковой;
• неравные – в каждой группе ширина интервала различна; при этом ее изменение может изменяться закономерно (например, равномерно возрастать), или произвольно, то есть быть свободной;

• закрытые - если известны верхняя и нижняя границы интервалов (максимальное и минимальное значения признака в группах);
• открытые - если известна только одна граница интервала, верхняя или нижняя.

Основные приемы построения и выполнения группировок
Если для построения группировки используется только один признак, то такую группировку называются простой, если группировка проводится по нескольким признакам, ее называют сложной. Сложная группировка бывает или комбинационная, или многомерная.

Комбинационная группировка выполняется последовательно: группы, выделенные по одному признаку, затем выделяются в подгруппы по другому признаку, которые, в свою очередь, могут выделяться по следующему другому признаку.

В этом случае число групп будет равно произведению числа выделенных групп на число группировочных признаков. Процедура определения оптимального числа групп основана на применении формулы Стерджесса
n=1+3,332*lg(N)(3.1)
где n - число групп; N - число единиц совокупности.

Из формулы видно, что выбор числа групп зависит от объема совокупности. Если групп оказывается много и они включают малое число единиц, то групповые показатели могут стать ненадежными. Поэтому альтернативой комбинационной группировке является многомерная группировка, которая осуществляется по комплексу признаков одновременно.

Ее применение требует использования электронной вычислительной техники. С помощью специально разработанных электронных программ формируются однородные группы на основании близости по всему комплексу признаков.

Определение числа групп тесно связано с понятием величина интервала: чем больше число групп, тем меньше величина интервала, и наоборот. Интервал - разница между максимальным и минимальным значениями признака в каждой группе.

Он определяет количественные границы групп, что для статистической практики имеет большое значение, особенно когда нужно образовать качественно однородные группы. Например, исследуется совокупность предприятий по выполнению коллективных договоров. Здесь нельзя объединять предприятия, которые не выполнили обязательства, и те, которые их перевыполнили. Показатель здесь - величина интервала.

Другим примером является невозможность образовывать группу 95 - 105%, поскольку это разные части совокупности. Следует образовать две группы: 95 - 100% и 101 - 105%. В этом случае границы, по которым различаются совокупности, абсолютно соблюдаются.

Каждый интервал имеет нижнюю (наименьшее значение признака) и верхнюю (наибольшее значение признака) границы или одну из них. Поэтому величина интервала есть разность между верхней и нижней границами интервала. Если у интервала указана лишь одна граница (у первого - верхняя, у последнего - нижняя), то речь идет об открытых интервалах.

Если у интервала имеются и нижняя, и верхняя границы, то речь идет о закрытых интервалах. Закрытые интервалы подразделяются на равные и неравные (прогрессивно возрастающие, прогрессивно убывающие), а также специализированные и произвольные.

Группировку с равными интервалами строят тогда, когда исследуются количественные различия в величине признака внутри групп одинакового качества, а также если распределение носит более или менее равномерный характер. Если можно заранее установить определенное количество групп, то величину равного интервала можно вычислить по формуле
T=(X max-X min)/n (3.2)

T=(X max-X min)/(1,000+3,322*lgn) (3.3)
где i - величина равного интервала; xmax , xmin - наибольшее и наименьшее значения признака; n - число групп.

Если величина равного интервала рассчитывается по данной формуле, то следует знаменатель предварительно округлить до целого числа (как правило, всегда большего), так как количество групп не может быть дробным числом.

В статистической практике чаще применяются неравные интервалы (постепенно возрастающие или постепенно убывающие). При этом исследуемая совокупность делится на группы примерно равного заполнения с большим числом единиц. Неравные интервалы могут использоваться, например, в таких случаях:

а) при исследовании группировки с применением нескольких признаков, дающих возможность составить несколько подгрупп, где требуются уже и более длинные и более короткие интервалы;
б) при образовании крупных групп с новым качеством на базе мелких групп при условии сохранения их однородности, что приводит к увеличению интервалов.

В статистической практике используются также специализированные интервалы. Интервалы называют специализированными, если речь идет об установлении границ интервала в группах, схожих по типу и по признаку, но имеющих отношение, скажем, к разным отраслям производства.

Виды группировок. Статистическая таблица
Виды группировок зависят от целей и задач, которые они выполняют. С помощью метода статистических группировок выделяют качественно однородные совокупности, изучают структуры совокупности и изменения, происходящие в них, а также решают задачи по исследованию существующих связей и зависимостей.

С известной мерой условности для выполнения этих задач группировки соответственно делят на типологические, структурные и аналитические.

Метод типологической группировки заключается в выявлении в качественно разнородной совокупности однородных групп. При этом очень важно правильно отобрать группировочный признак, который поможет идентифицировать выбранный тип. Типологические группировки широко применяются в исследовании социально- экономических явлений.

Примерами такого вида группировок могут быть группы предприятий по формам собственности (табл. 3.1), по формам хозяйствования, социальные группы населения и т.д. В типологических группировках часто используются специализированные интервалы.

Группировка полиграфических предприятий
одного из городов России
по формам собственности

Метод структурной группировки есть разделение однородной совокупности на группы по тому или иному варьирующему группировочному признаку. Примерами такого вида группировок могут быть группы населения по полу, возрасту, месту проживания, доходу и т.д.,

то есть может решаться задача по изучению структурного состава той или иной однородной совокупности, структурных изменений по тому или иному группировочному признаку. На основе структурных изменений изучаются закономерности общественных явлений (табл. 3.2).

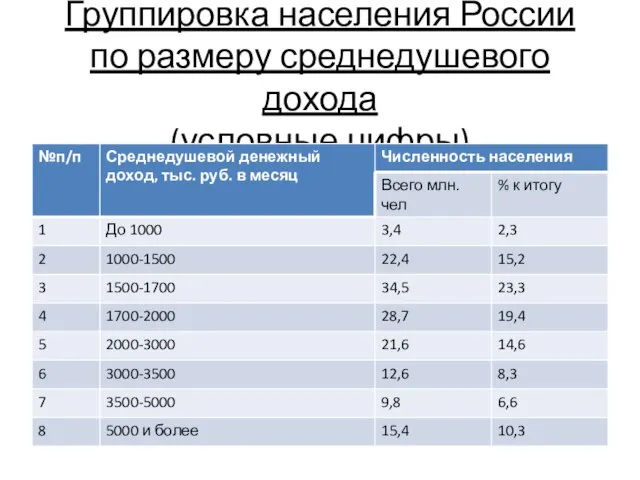
Группировка населения России
по размеру среднедушевого дохода
(условные цифры)

Метод аналитической группировки заключается в исследовании взаимосвязей между факторными признаками в качественно однородной совокупности. С помощью аналитических группировок удается выявлять признаки, которые могут выступать или причиной, или следствием того или иного явления.

В аналитических группировках чаще всего используются неравные интервалы. Пример аналитической группировки представлен в табл. 3.3.

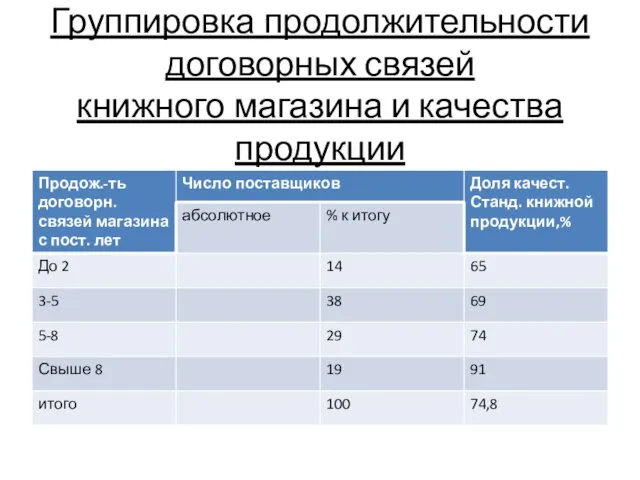
Группировка продолжительности договорных связей
книжного магазина и качества продукции

Результаты группировочного материала оформляются в виде таблиц, где он излагается в наглядно-рациональной форме. Не всякая таблица может быть статистической. Табличные формы календарей, тестовых и опросных листов, таблица умножения не являются статистическими.

Статистическая таблица - это цифровое выражение итоговой характеристики всей наблюдаемой совокупности или ее составных частей по одному или нескольким существенным признакам. Статистическая таблица содержит два элемента: подлежащее и сказуемое.
Подлежащее статистической таблицы есть перечень групп или единиц, составляющих исследуемую совокупность единиц наблюдения.

Сказуемое статистической таблицы - это цифровые показатели, с помощью которых дается характеристика выделенных в подлежащем групп и единиц.
Различают простые, групповые и комбинационные таблицы.

простых таблицах, как правило, содержится справочный материал, где дается перечень групп или единиц, составляющих объект изучения. При этом части подлежащего не являются группами одинакового качества, отсутствует систематизация изучаемых единиц. Сказуемое этих таблиц содержит абсолютные величины, отражающие объемы изучаемых процессов.

Групповые и комбинационные таблицы предназначены для научных целей, где, в отличие от простых таблиц, в сказуемом - средние и относительные величины на основе абсолютных величин.

Групповая таблица - это таблица, где статистическая совокупность разбивается на отдельные группы по какому-либо одному существенному признаку, при этом каждая группа характеризуется рядом показателей. Примером такой группировки может быть разделение российских семей на группы по месту проживания (сельское и городское), где образуются подгруппы семей по количеству детей. Анализ этих группировок по материалам переписи 1989 года позволил сделать вывод, что большинство семей, независимо от принадлежности к городскому или сельскому населению, имеют только по одному ребенку.

Комбинационная таблица - это таблица, где подлежащее представляет собой группировку единиц совокупности по двум и более признакам, которые распределяются на группы сначала по одному признаку, а затем на подгруппы по другому признаку внутри каждой из уже выделенных групп. Комбинационная таблица устанавливает существенную связь между факторами группировки.

Примером комбинационной группировки может быть распределение полиграфических предприятий по трем существенным признакам: степени оснащенности современным полиграфическим оборудованием, степени применения современных технологий и уровню производительности труда. Такого рода статистические таблицы позволяют осуществить всесторонний анализ, но они менее наглядны.

При составлении таблиц необходимо соблюдать общие правила:
таблица должна быть легко обозримой;
общий заголовок должен кратко выражать основное содержание;
наличие строк «общих итогов»;
наличие нумерации строк, которые заполняются данными;
соблюдение правила округления чисел.

Динамический ряд - последовательность числовых значений (уровней), характеризующих развитие во времени какого-либо признака исторического явления.

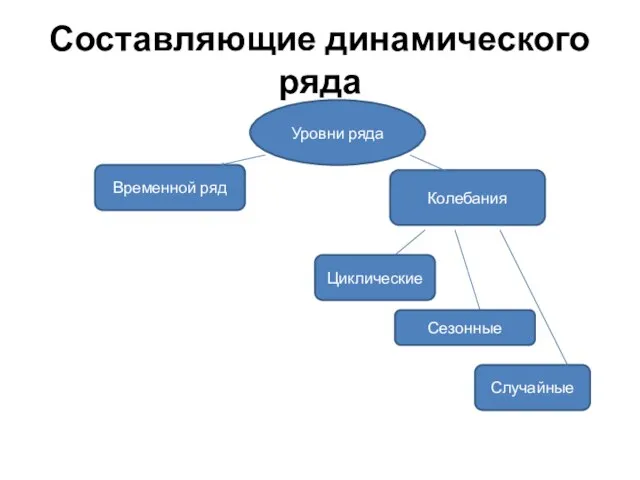
Составляющие динамического ряда
Уровни ряда
Временной ряд
Колебания
Циклические
Сезонные
Случайные

Уровни ряда - числовые значения признака, характеризующие его состояние в определенный

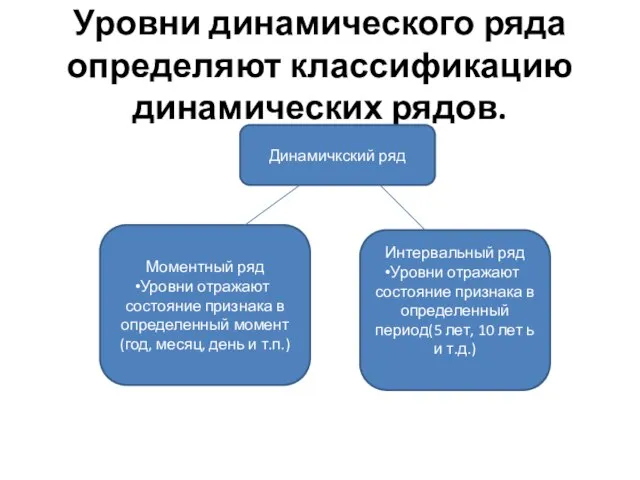
Уровни динамического ряда определяют классификацию динамических рядов.
Динамичкский ряд
Моментный ряд
Уровни отражают состояние признака в определенный момент(год, месяц, день и т.п.)
Интервальный ряд
Уровни отражают состояние признака в определенный период(5 лет, 10 лет ь и т.д.)