Прямоугольная система координат в пространстве. Координаты середины отрезка. Расстояние между двумя точками. Уравнение сферы
Содержание
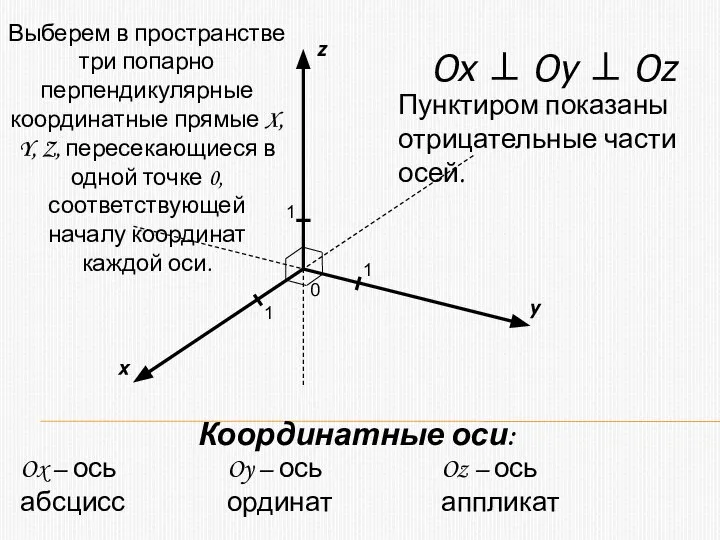
- 2. Как задать прямоугольную систему координат в пространстве?
- 3. Тема 13.4. Прямоугольная система координат в пространстве. Координаты середины отрезка. Расстояние между двумя точками. Уравнение сферы
- 4. x y z 0 1 Ox ⊥ Oy ⊥ Oz Ox – ось абсцисс Oy –
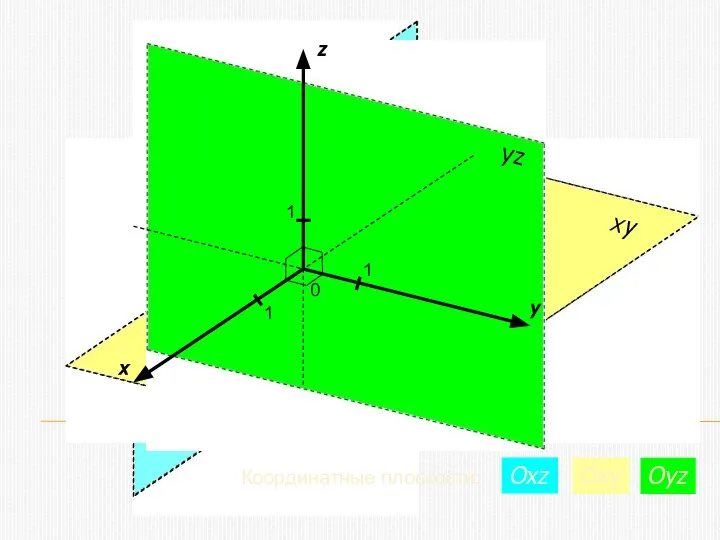
- 5. x y z 0 1 1 1 Координатные плоскости: Oxz Oxy Oyz
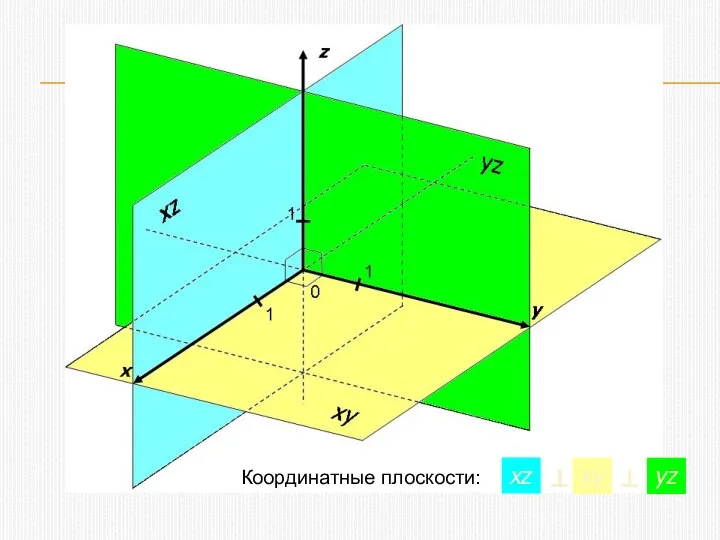
- 6. Координатные плоскости: xz ⊥ xy ⊥ yz
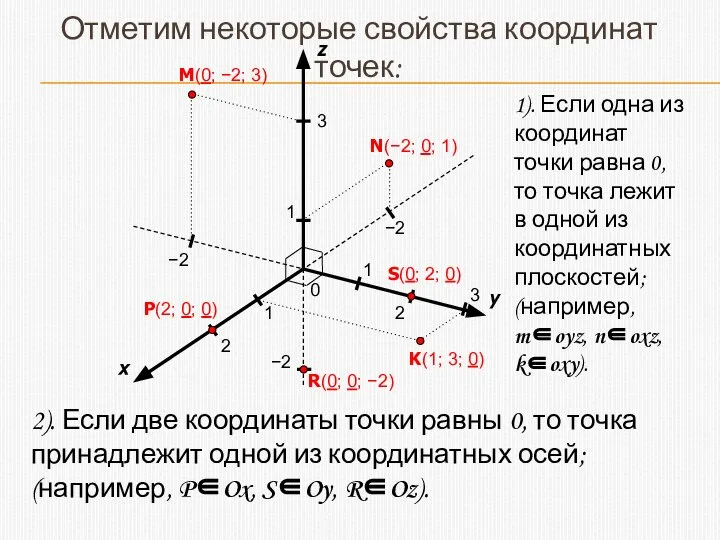
- 7. Как определить положение точки в пространстве?
- 8. 1). Если одна из координат точки равна 0, то точка лежит в одной из координатных плоскостей;
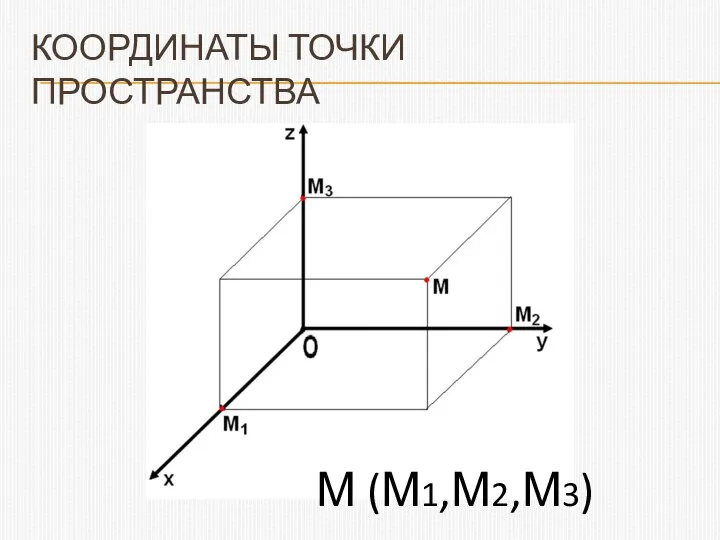
- 9. КООРДИНАТЫ ТОЧКИ ПРОСТРАНСТВА М (М1,М2,М3)
- 10. Расстояние между точками A(x1; y1; z1) и B(x2; y2; z2) Координаты середины отрезка АВ, где A(x1;
- 11. Задача Дано: А (1;-1;2), В (3;1;-2) Найдите координаты середины отрезка АВ и его длину.
- 12. Решение: Найдем координаты середины отрезка Теперь найдем отрезок AB
- 16. Скачать презентацию








 Презентация на тему Числовые выражения 7 класс
Презентация на тему Числовые выражения 7 класс  Тригонометрические функции
Тригонометрические функции Системы нелинейных неравенств с двумя переменными
Системы нелинейных неравенств с двумя переменными Целостный подход. Производная функции y=f'(x)
Целостный подход. Производная функции y=f'(x) СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ
СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ Последовательности и прогрессии (ПР №25)
Последовательности и прогрессии (ПР №25) Неравенства с двумя переменными
Неравенства с двумя переменными Новые счётные единицы. Класс единиц и класс тысяч
Новые счётные единицы. Класс единиц и класс тысяч Сочетание традиций и инноваций в учебниках математики Н. Я. Виленкина – залог успешного обучения
Сочетание традиций и инноваций в учебниках математики Н. Я. Виленкина – залог успешного обучения Перехідна та імпульсна перехідна функції
Перехідна та імпульсна перехідна функції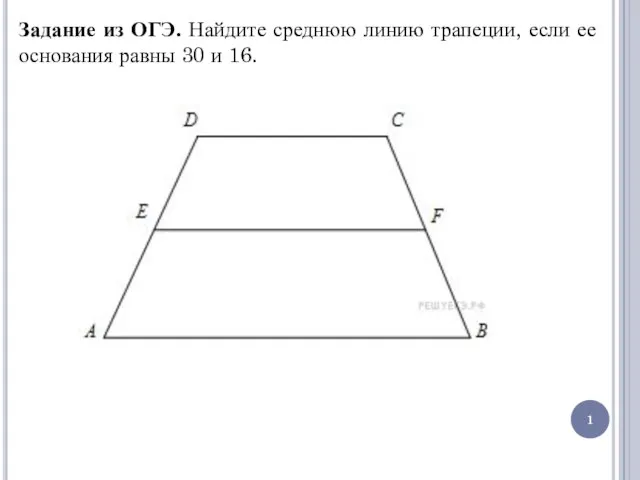 Прямоугольник. Ромб. Квадрат. Задание из ОГЭ
Прямоугольник. Ромб. Квадрат. Задание из ОГЭ Рефлексия. Задачи. Домашняя работа
Рефлексия. Задачи. Домашняя работа Волшебная страна - Геометрия
Волшебная страна - Геометрия Десятичные и натуральные логарифмы. Формула перехода к другому основанию
Десятичные и натуральные логарифмы. Формула перехода к другому основанию Сайы. Умумий малюмат
Сайы. Умумий малюмат Элементы математического анализа
Элементы математического анализа Сумма углов треугольника
Сумма углов треугольника Сравнение числовых выражений (Урок 30)
Сравнение числовых выражений (Урок 30) Methodical Problems of Comparative Studies
Methodical Problems of Comparative Studies Отбор корней в тригонометрических уравнениях. Уравнения, имеющие ограничения в области определения
Отбор корней в тригонометрических уравнениях. Уравнения, имеющие ограничения в области определения Вторая производная и её физический смысл
Вторая производная и её физический смысл Число и цифра 3
Число и цифра 3 Разложение квадратного трёхчлена на множители
Разложение квадратного трёхчлена на множители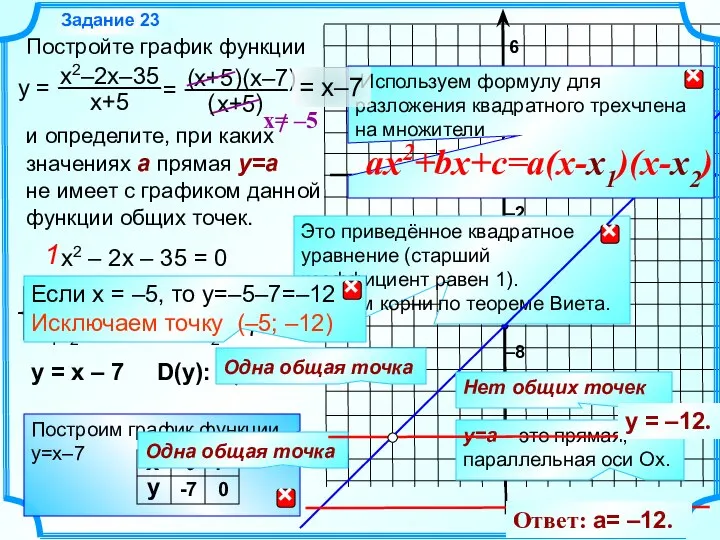 Прямая. Часть II
Прямая. Часть II Медианы, биссектрисы и высота треугольника
Медианы, биссектрисы и высота треугольника Симметрия. Виды симметрии
Симметрия. Виды симметрии Виды углов
Виды углов Основы теории вероятностей и математической статистики
Основы теории вероятностей и математической статистики