Содержание
- 2. Окружность Надо вспомнить: • ОКРУЖНОСТЬ И КРУГ • СВОЙСТВА ХОРД • УГЛЫ И ОКРУЖНОСТЬ • ВПИСАННЫЕ
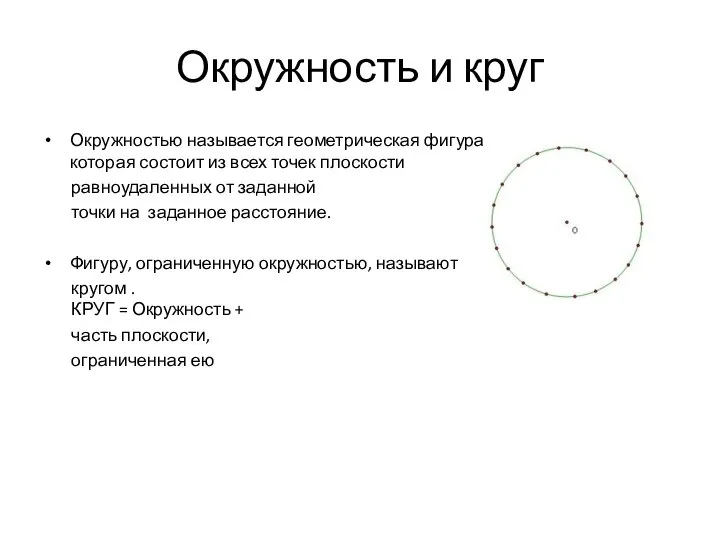
- 3. Окружностью называется геометрическая фигура, которая состоит из всех точек плоскости равноудаленных от заданной точки на заданное
- 4. Свойства хорд Если хорды равноудалены от центра окружности, то они равны. Если хорды равны, то они
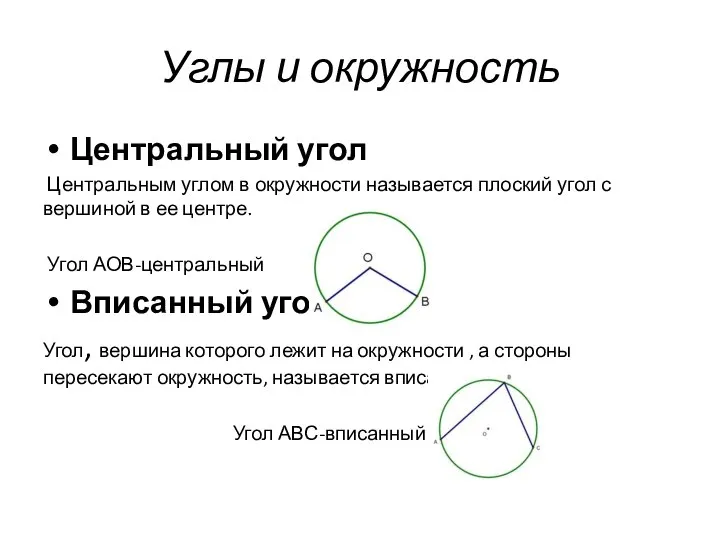
- 5. Углы и окружность Центральный угол Центральным углом в окружности называется плоский угол с вершиной в ее
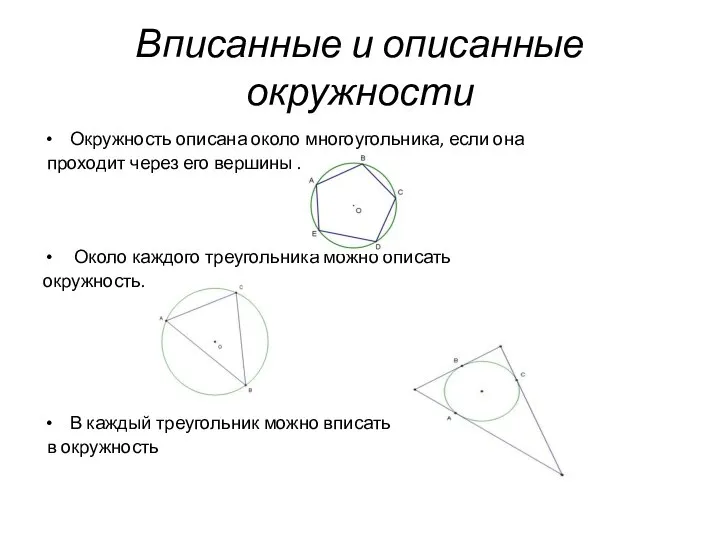
- 6. Вписанные и описанные окружности Окружность описана около многоугольника, если она проходит через его вершины . Около
- 7. Длины и площади
- 8. Четырехугольники Многоугольники Параллелограмм и трапеция Прямоугольник, ромб, квадрат Площадь Теорема Пифагора
- 9. Многоугольники Многоугольник Смежные отрезки-это пара пересекающихся отрезков, не лежащих на одной прямой. Диагональ-отрезок, соединяющий любые две
- 10. Параллелограмм и трапеция Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны. В параллелограмме противоположные стороны
- 11. Прямоугольник, ромб,квадрат Прямоугольником называется параллелограмм, у которого все углы прямые. Диагонали прямоугольника равны. Если в параллелограмме
- 12. Площадь Равные многоугольники имеют равные площади. Если многоугольник составлен из нескольких многоугольников, то его площадь равна
- 13. Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
- 14. Треугольники Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны этого треугольника. Медиана
- 15. Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит
- 16. Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника. В
- 17. Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку. Каждая точка серединного
- 19. Скачать презентацию













 Преемственность в формировании УПК младших школьников и учащихся 5-6 классов на уроках математики посредством интеграции
Преемственность в формировании УПК младших школьников и учащихся 5-6 классов на уроках математики посредством интеграции Геометрия Евклида
Геометрия Евклида Почему нельзя делить на ноль
Почему нельзя делить на ноль Определение синуса, косинуса, тангенса острого угла прямоугольного треугольника
Определение синуса, косинуса, тангенса острого угла прямоугольного треугольника Точка, отрезок, луч, прямая
Точка, отрезок, луч, прямая Интерактивная дидактическая игра Состав чисел до 10. Математика, 1 класс
Интерактивная дидактическая игра Состав чисел до 10. Математика, 1 класс Презентация на тему Дробные выражения (6 класс)
Презентация на тему Дробные выражения (6 класс)  Правило Лопиталя. Семинар 17
Правило Лопиталя. Семинар 17 Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля
Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля 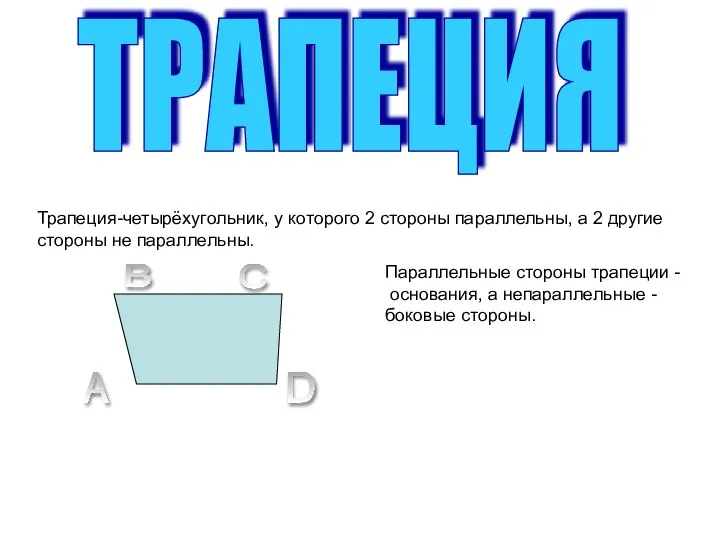 Трапеция
Трапеция Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Общее уравнение прямой и плоскости. Лекция1 (1)
Общее уравнение прямой и плоскости. Лекция1 (1) Умножение и деление десятичных дробей на натуральное число
Умножение и деление десятичных дробей на натуральное число Презентация на тему Понятие одночлена стандартный вид одночлена (7 класс)
Презентация на тему Понятие одночлена стандартный вид одночлена (7 класс)  Второй признак равенства треугольников. Урок 16
Второй признак равенства треугольников. Урок 16 Соотношения между сторонами и углами прямоугольного треугольника. Синус, косинус, тангенс и котангенс острого угла
Соотношения между сторонами и углами прямоугольного треугольника. Синус, косинус, тангенс и котангенс острого угла Решение примеров и уравнений
Решение примеров и уравнений L_3_U
L_3_U Презентация по математике "Число 5. Цифра 5" -
Презентация по математике "Число 5. Цифра 5" -  Цилиндр
Цилиндр Fraktaly_Osnovnye_ponyatia (1)
Fraktaly_Osnovnye_ponyatia (1) Действительные числа
Действительные числа Задача на внимание. 5 класс
Задача на внимание. 5 класс Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота
Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота Площадь параллелограмма
Площадь параллелограмма Умножение двузначных чисел
Умножение двузначных чисел Число 5
Число 5 Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей