Содержание
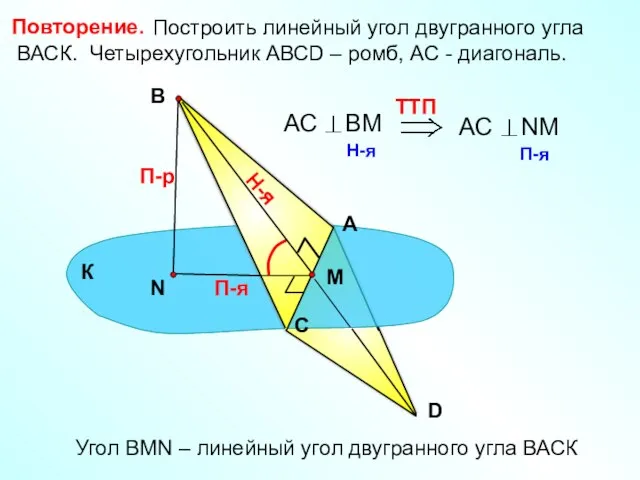
- 2. Построить линейный угол двугранного угла ВАСК. Четырехугольник АВСD – ромб, АС - диагональ. А С В
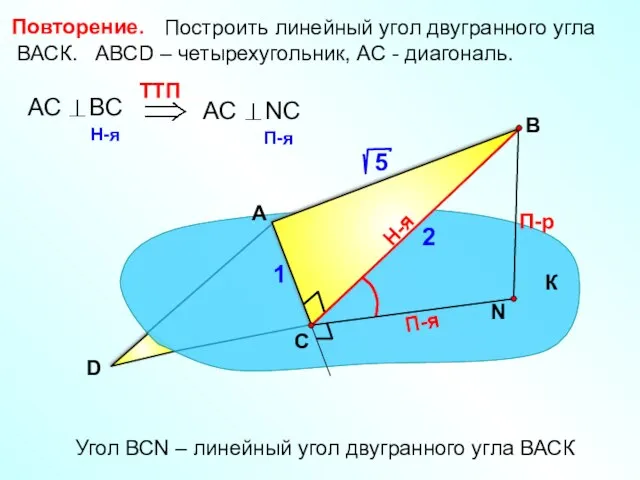
- 3. Построить линейный угол двугранного угла ВАСК. АВСD – четырехугольник, АС - диагональ. А В П-р Н-я
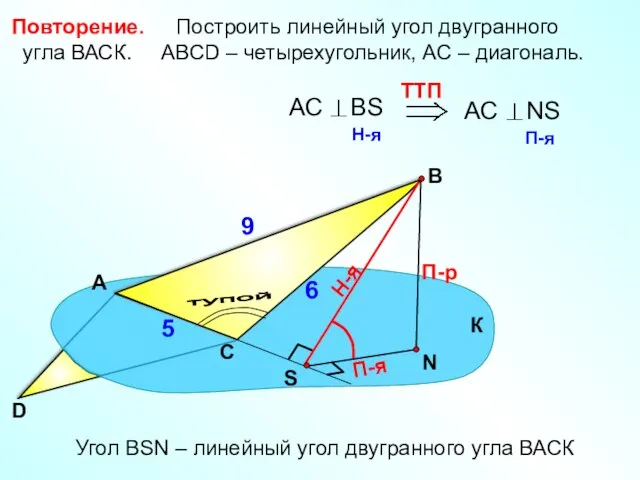
- 4. Построить линейный угол двугранного угла ВАСК. АВСD – четырехугольник, АС – диагональ. А В П-р Н-я
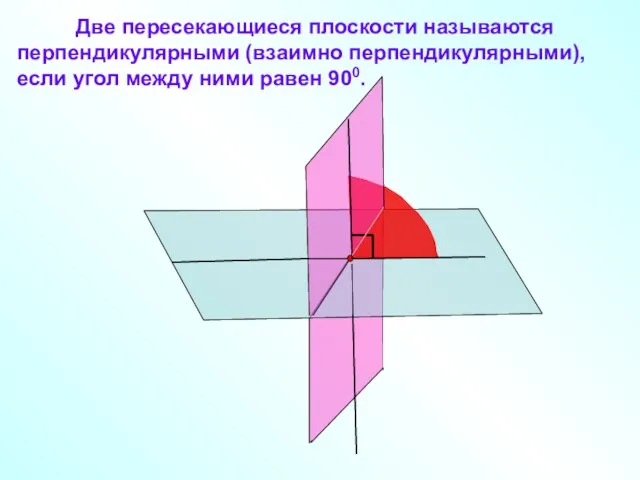
- 5. Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 900.
- 6. Примером взаимно перпендикулярных плоскостей служат плоскости стены и пола комнаты, плоскости стены и потолка.
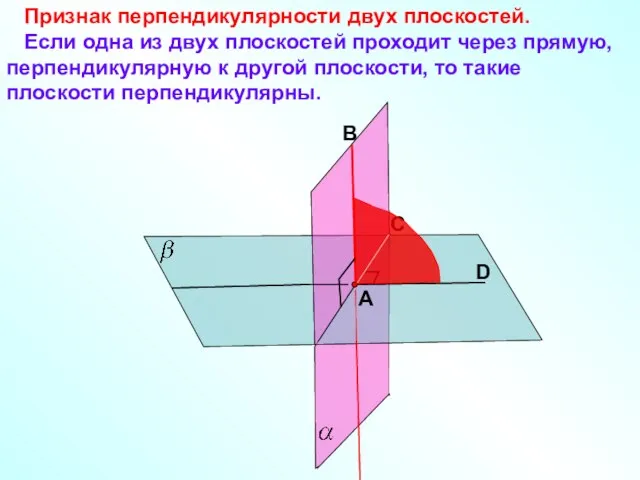
- 7. Признак перпендикулярности двух плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости,
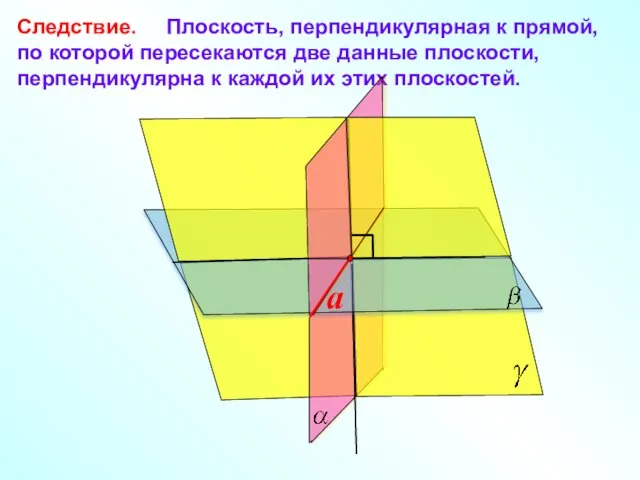
- 8. Следствие. Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой их этих
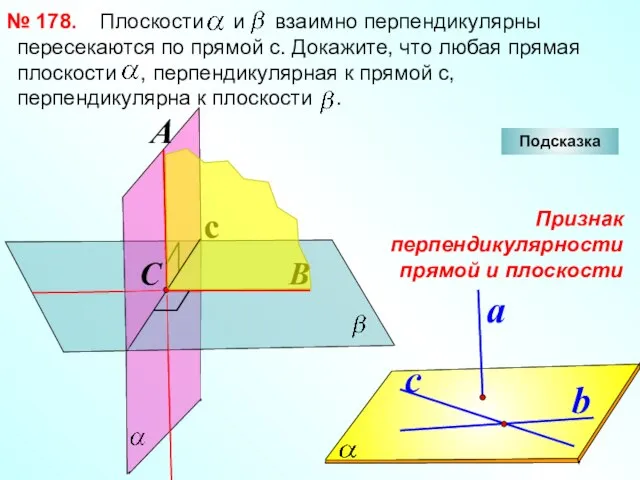
- 9. Плоскости и взаимно перпендикулярны пересекаются по прямой с. Докажите, что любая прямая плоскости , перпендикулярная к
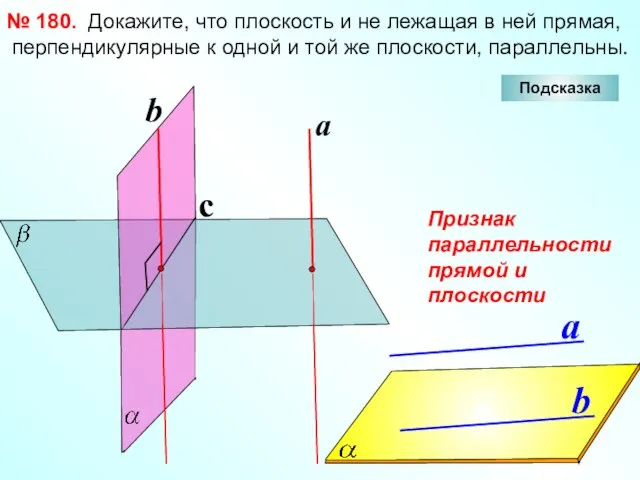
- 10. Докажите, что плоскость и не лежащая в ней прямая, перпендикулярные к одной и той же плоскости,
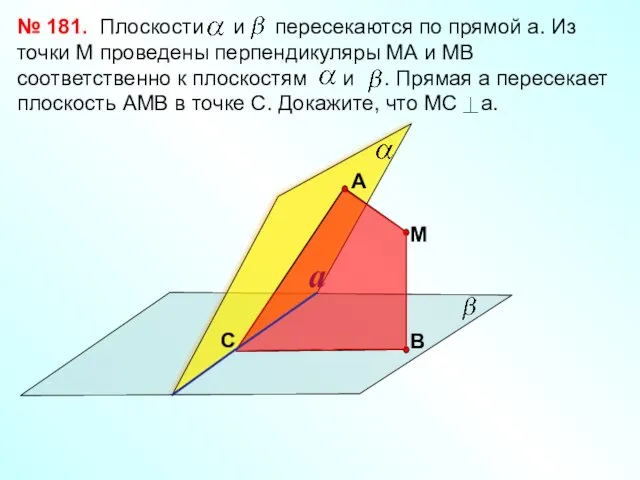
- 11. № 181. С М a
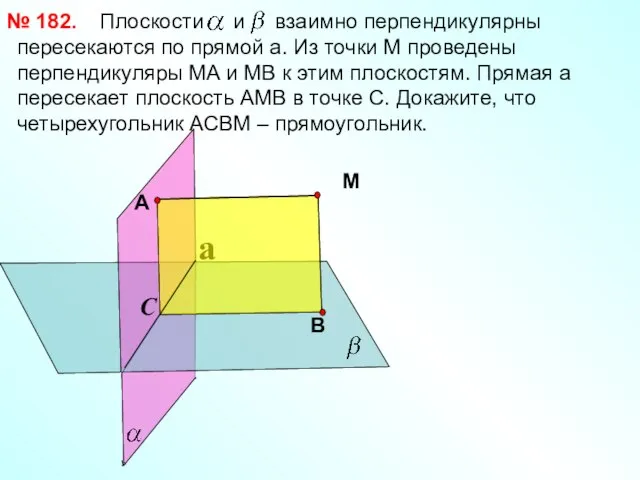
- 12. Плоскости и взаимно перпендикулярны пересекаются по прямой a. Из точки М проведены перпендикуляры МА и МВ
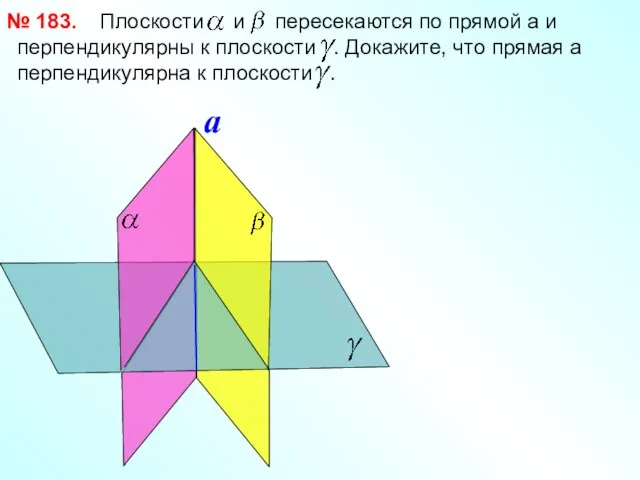
- 13. Плоскости и пересекаются по прямой a и перпендикулярны к плоскости . Докажите, что прямая а перпендикулярна
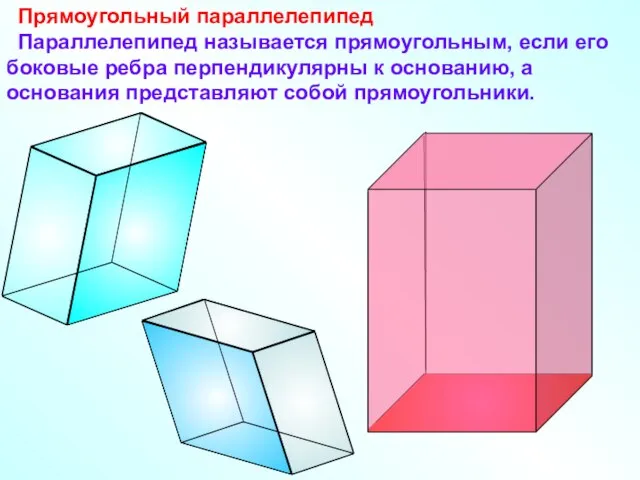
- 14. Прямоугольный параллелепипед Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой
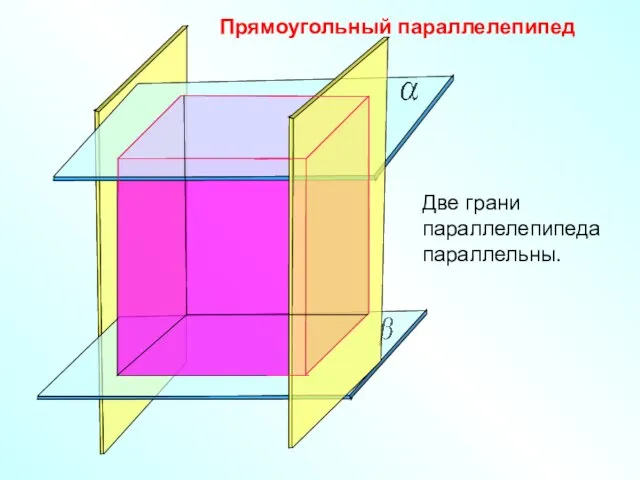
- 15. Прямоугольный параллелепипед Две грани параллелепипеда параллельны.
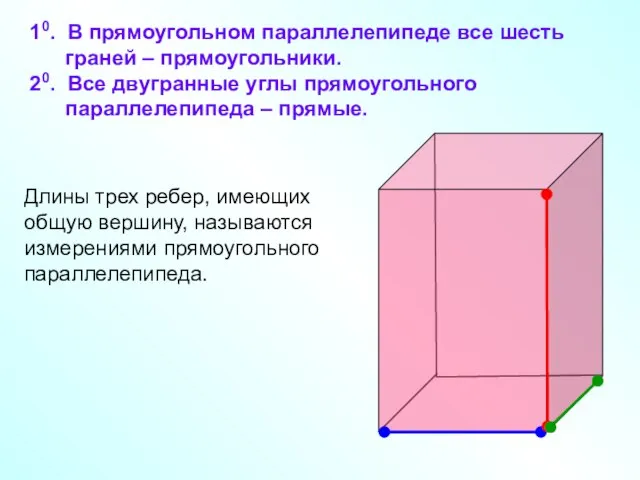
- 16. 10. В прямоугольном параллелепипеде все шесть граней – прямоугольники. 20. Все двугранные углы прямоугольного параллелепипеда –
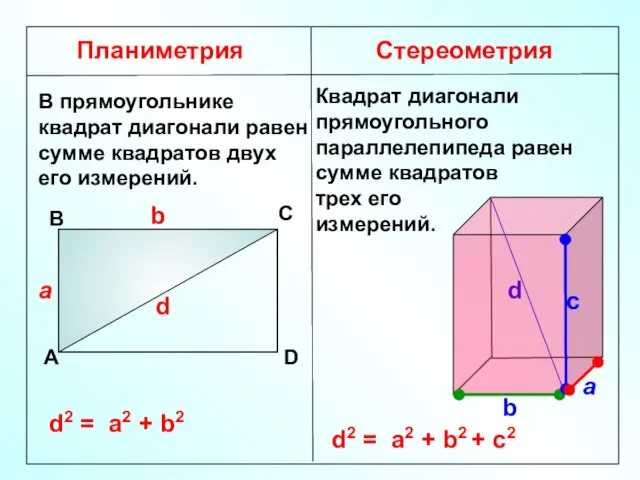
- 17. Планиметрия Стереометрия В прямоугольнике квадрат диагонали равен сумме квадратов двух его измерений. А В С D
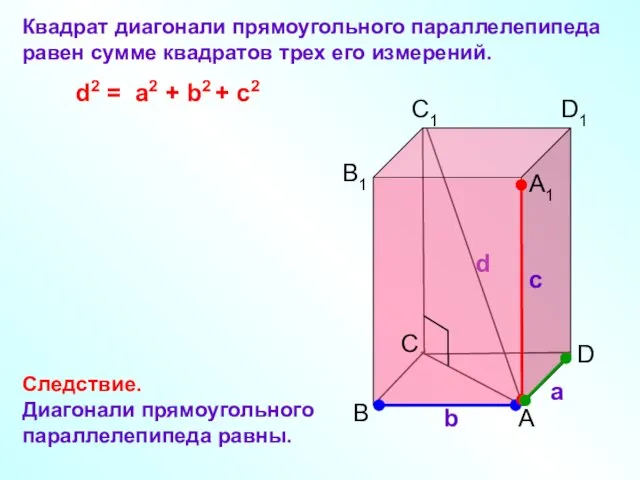
- 18. C а b с B A D B1 C1 D1 A1 Квадрат диагонали прямоугольного параллелепипеда равен
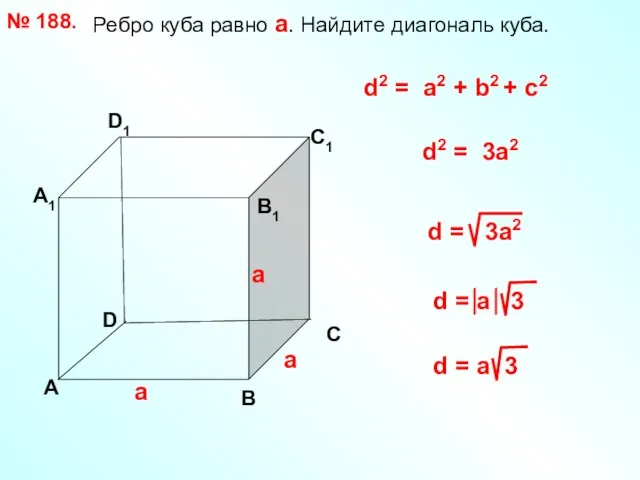
- 19. Ребро куба равно а. Найдите диагональ куба. № 188. D А В С А1 D1 С1
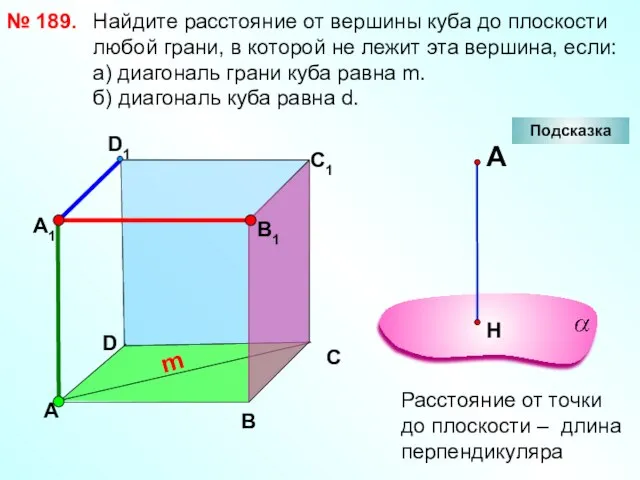
- 20. Найдите расстояние от вершины куба до плоскости любой грани, в которой не лежит эта вершина, если:
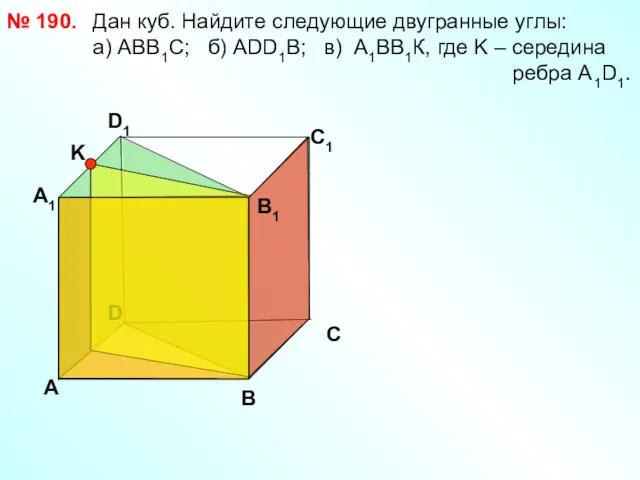
- 21. Дан куб. Найдите следующие двугранные углы: a) АВВ1С; б) АDD1B; в) А1ВВ1К, где K – середина
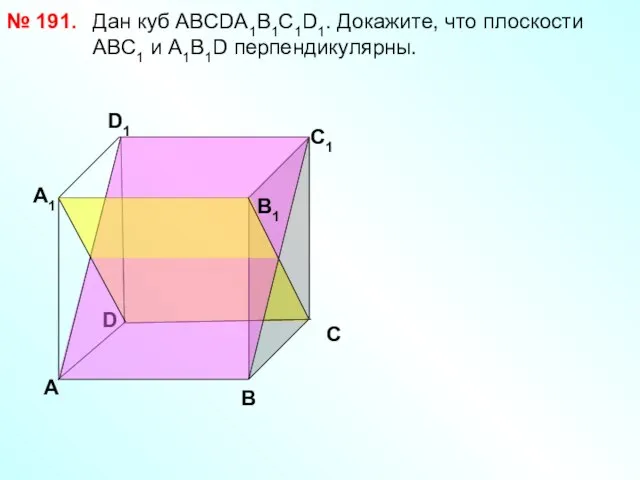
- 22. Дан куб АВСDА1В1С1D1. Докажите, что плоскости АВС1 и А1В1D перпендикулярны. № 191. D А В С
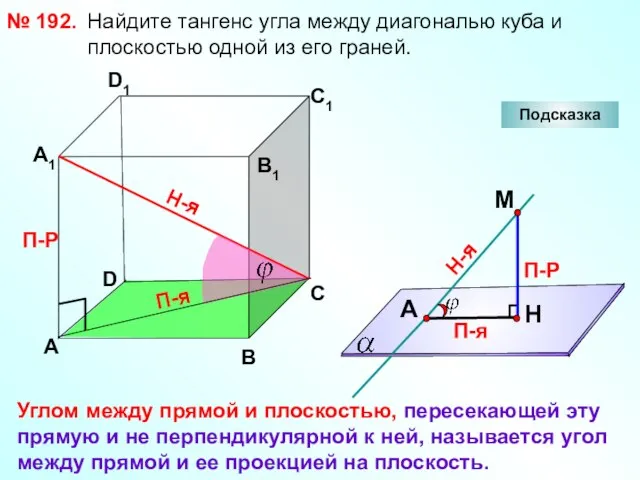
- 23. Найдите тангенс угла между диагональю куба и плоскостью одной из его граней. № 192. D А
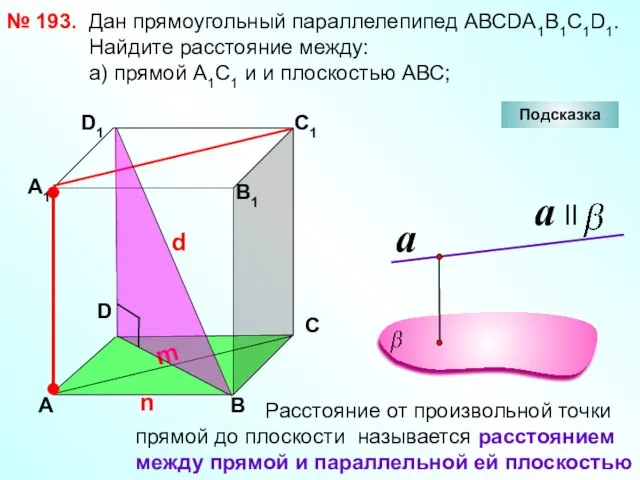
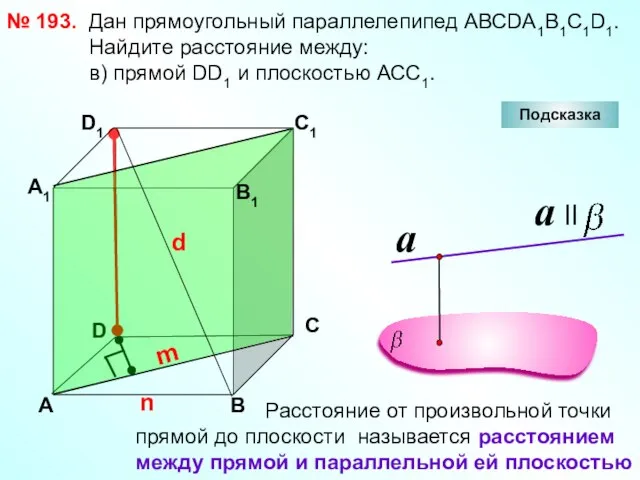
- 24. № 193. D А В С А1 D1 С1 В1 Подсказка Дан прямоугольный параллелепипед АВСDА1В1С1D1. Найдите
- 25. № 193. D А В С А1 D1 С1 В1 Подсказка Дан прямоугольный параллелепипед АВСDА1В1С1D1 Найдите
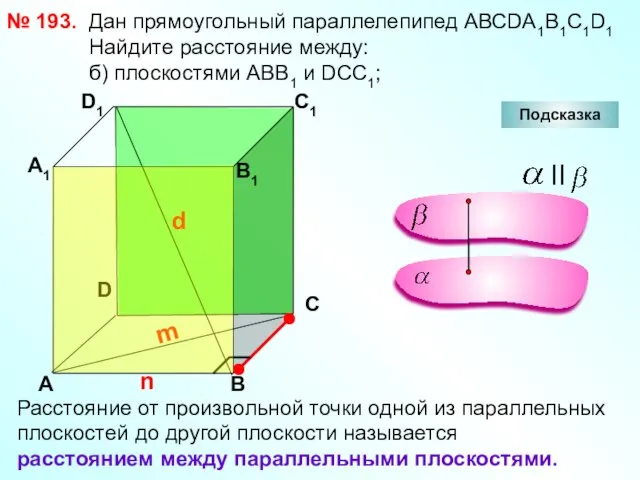
- 26. № 193. D А В С А1 D1 С1 Дан прямоугольный параллелепипед АВСDА1В1С1D1. Найдите расстояние между:
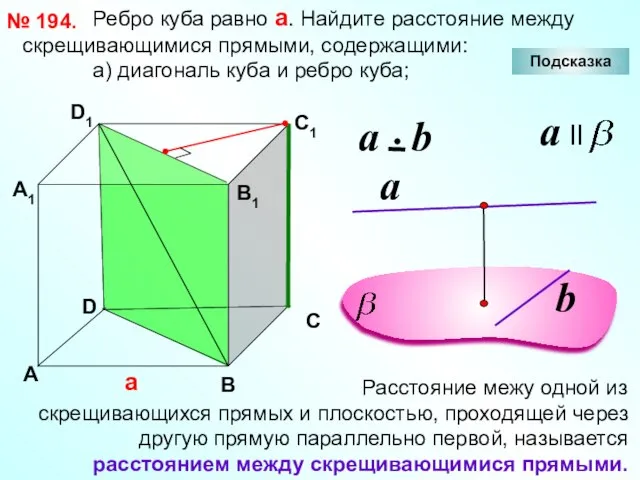
- 27. Ребро куба равно а. Найдите расстояние между скрещивающимися прямыми, содержащими: а) диагональ куба и ребро куба;
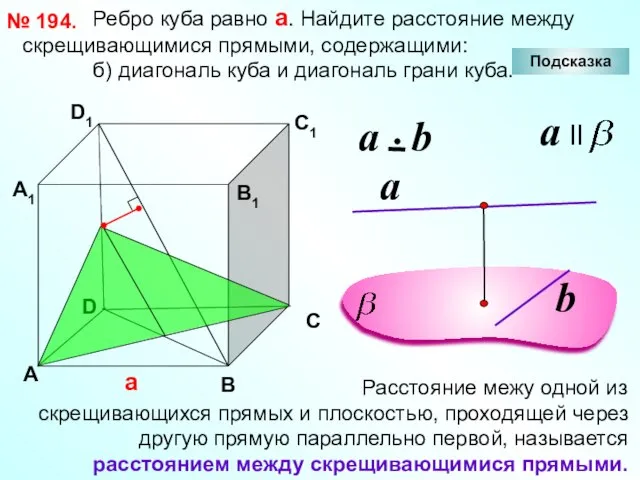
- 28. Ребро куба равно а. Найдите расстояние между скрещивающимися прямыми, содержащими: б) диагональ куба и диагональ грани
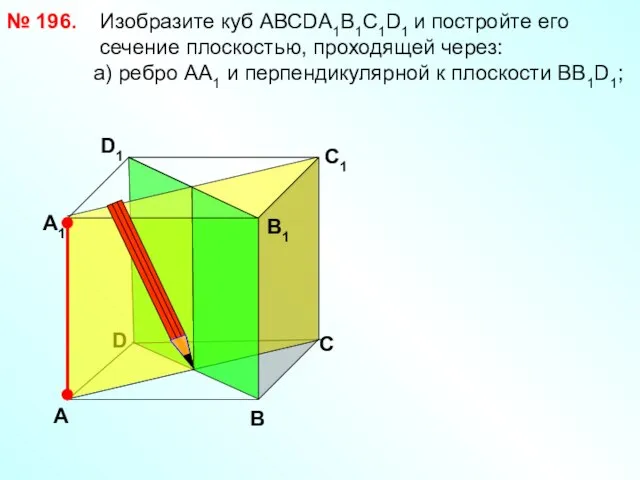
- 29. № 196. D В D1 С1 Изобразите куб АВСDА1В1С1D1 и постройте его сечение плоскостью, проходящей через:
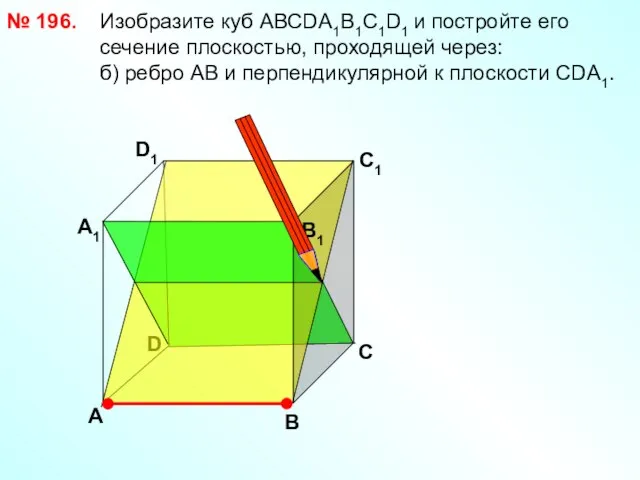
- 30. № 196. Изобразите куб АВСDА1В1С1D1 и постройте его сечение плоскостью, проходящей через: б) ребро АВ и
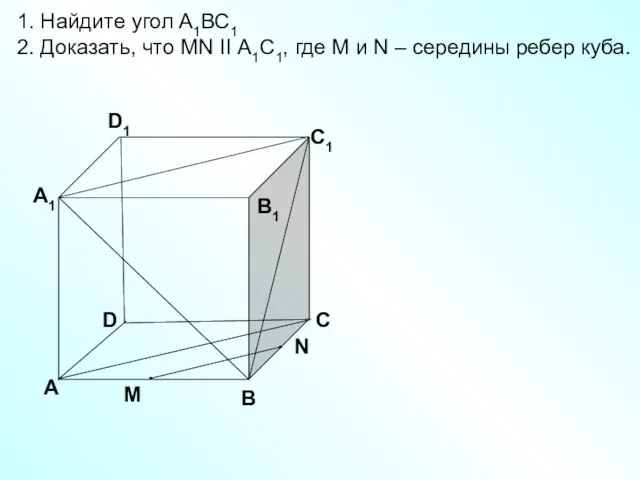
- 31. D А В С А1 D1 С1 В1 1. Найдите угол А1ВС1 2. Доказать, что MN
- 33. Скачать презентацию

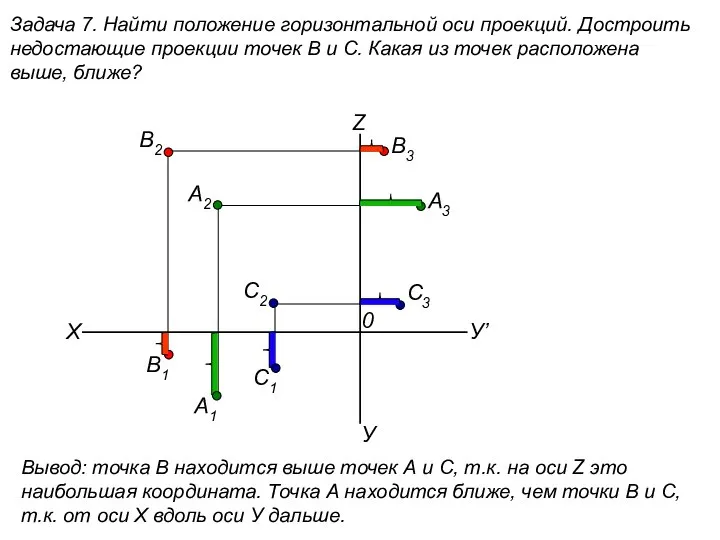 Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7)
Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7) LP (1)
LP (1)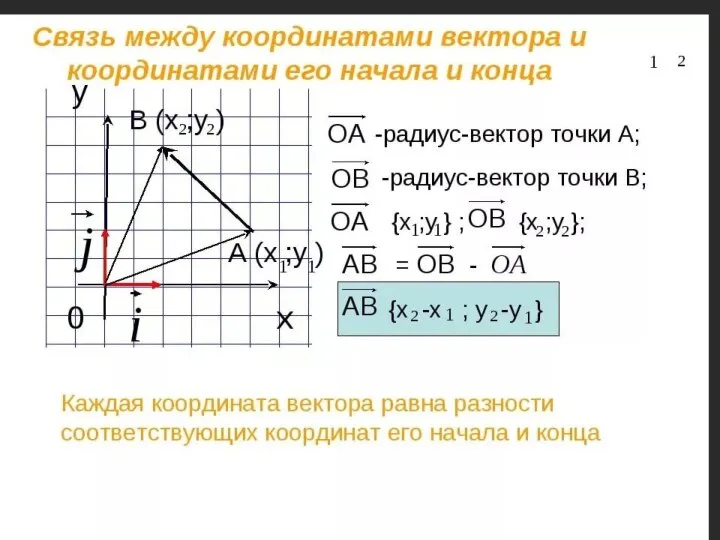 Векторы
Векторы Тест Проверь себя. ГИА (Четырёхугольники)
Тест Проверь себя. ГИА (Четырёхугольники) Решение задач. Урок №68
Решение задач. Урок №68 Геометрические места точек. (7 класс)
Геометрические места точек. (7 класс)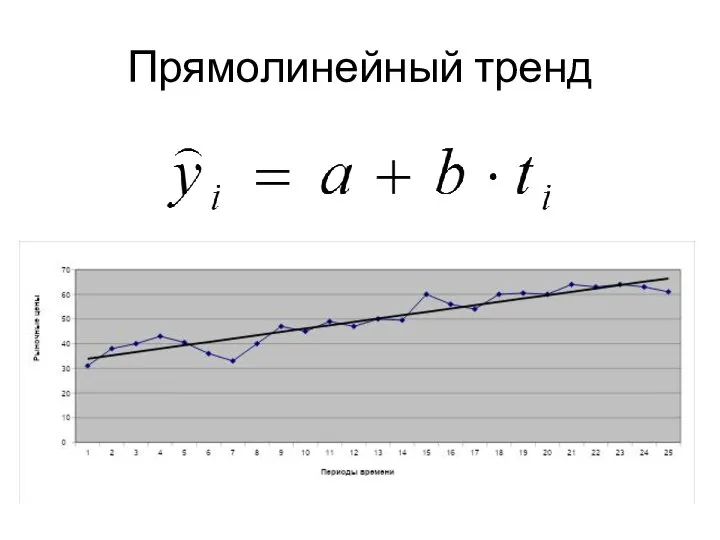 Прямолинейный тренд
Прямолинейный тренд Применение основных тригонометрических формул к решению уравнений
Применение основных тригонометрических формул к решению уравнений Булева алгебра. Семинар №2
Булева алгебра. Семинар №2 Презентация на тему Нумерация многозначных чисел (4 класс)
Презентация на тему Нумерация многозначных чисел (4 класс)  Сложение чисел
Сложение чисел Решение задач по теме Арифметическая прогрессия
Решение задач по теме Арифметическая прогрессия Взаимное расположение прямой и окружности, двух окружностей
Взаимное расположение прямой и окружности, двух окружностей Блиц-турнир по математике
Блиц-турнир по математике Многогранники. Прямоугольные параллелепипеды
Многогранники. Прямоугольные параллелепипеды Элективный курс. Алгебра 11 класс. Уроки 10
Элективный курс. Алгебра 11 класс. Уроки 10 Тема: 14 -
Тема: 14 - Организация исследовательской деятельности учащихся по математике
Организация исследовательской деятельности учащихся по математике Геометрические фигуры (интерактивная игра)
Геометрические фигуры (интерактивная игра) Взаимное расположение прямой и окружности. Касательная
Взаимное расположение прямой и окружности. Касательная Решение составных задач
Решение составных задач Геометрия. 8 класс
Геометрия. 8 класс Простейшие задачи в координатах
Простейшие задачи в координатах Основное свойство арифметического квадратного корня
Основное свойство арифметического квадратного корня Действия над векторами в пространстве
Действия над векторами в пространстве Применение распределительного свойства умножения
Применение распределительного свойства умножения Тождественные преобразования. 7 класс
Тождественные преобразования. 7 класс Математическая карусель
Математическая карусель