Содержание
- 2. ЗАДАЧА 2. Найти длину вектора, если известны его координаты в декартовом прямоугольном базисе. Оставьте 5 строчек
- 3. Геометрический смысл координат орта вектора Это равенство называют основным тождеством для направляющих косинусов вектора.
- 4. ЗАДАЧА 4. Известны координаты концов отрезка. Найти координаты точки, которая делит отрезок в заданном отношении. Если
- 5. §3. Нелинейные операции на множестве векторов СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ После каждого свойства оставьте 3-5 строк
- 6. 3) Числовой множитель любого из двух векторов можно вынести за знак скалярного произведения. Т.е. 4) Если
- 7. 5) Скалярное произведение вектора на себя (скалярный квадрат вектора) равно квадрату его длины. Т.е. Формулу (1)
- 8. 2. Векторное произведение векторов
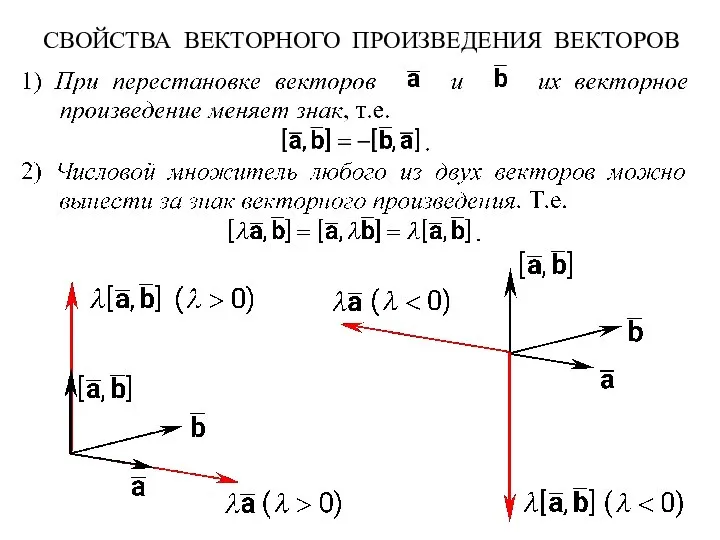
- 10. СВОЙСТВА ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
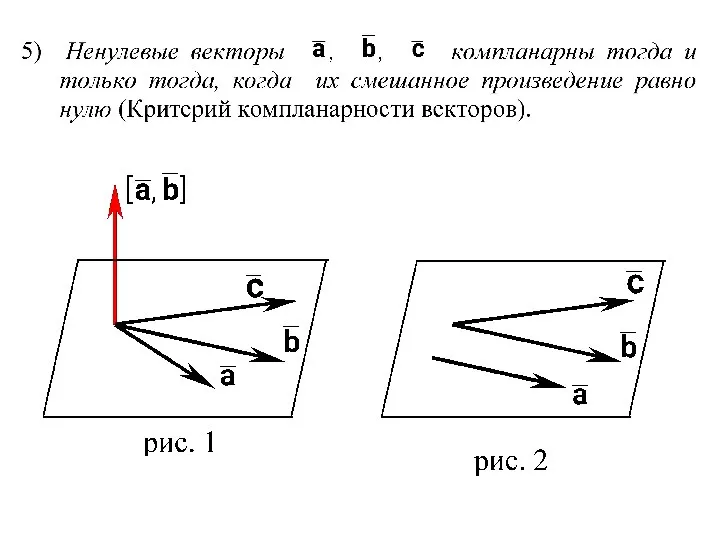
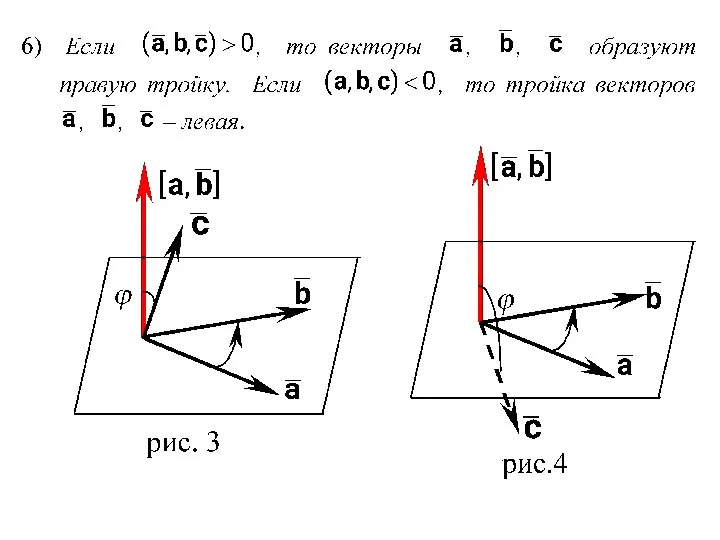
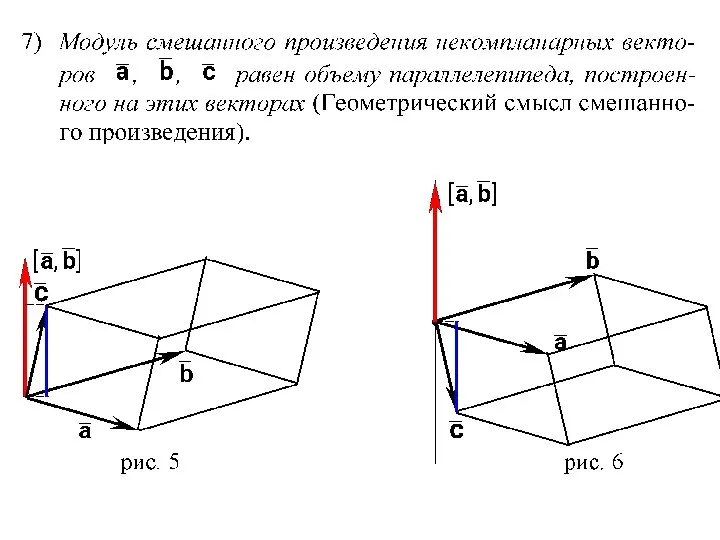
- 13. 3. Смешанное произведение векторов СВОЙСТВА СМЕШАННОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
- 19. Скачать презентацию












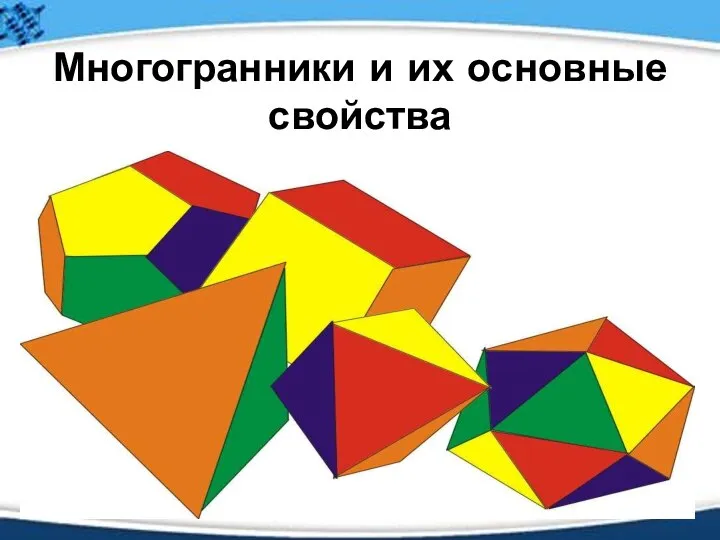 Многогранники и их основные свойства
Многогранники и их основные свойства Формула сложных процентов в ЕГЭ. 11 класс
Формула сложных процентов в ЕГЭ. 11 класс Сокращенное умножение многочленов
Сокращенное умножение многочленов Переместительный и сочетательный законы сложения
Переместительный и сочетательный законы сложения Практика. Дискретная математика
Практика. Дискретная математика Презентация на тему Софья Васильевна Ковалевская
Презентация на тему Софья Васильевна Ковалевская  Уравнение прямой
Уравнение прямой Сумма углов треугольника. Решение задач
Сумма углов треугольника. Решение задач Координаты вектора
Координаты вектора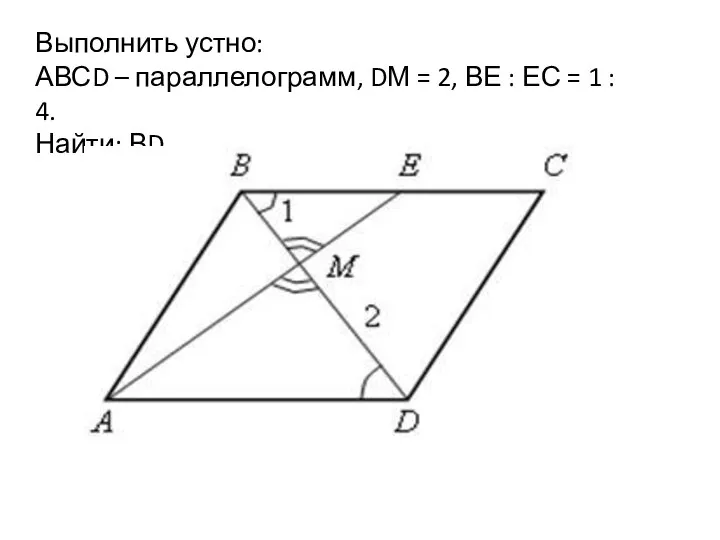 Принак подобия треугольников. Урок 33
Принак подобия треугольников. Урок 33 Миллиметр. В каких числах сумма цифр равна 5?
Миллиметр. В каких числах сумма цифр равна 5?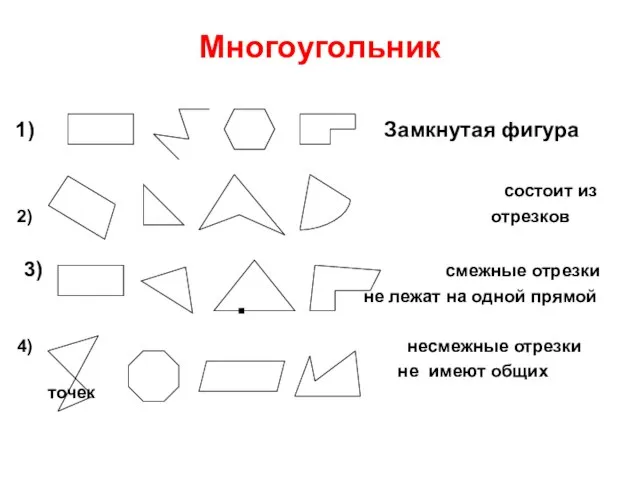 Классификация многоугольников по числу углов
Классификация многоугольников по числу углов Задача предельного типа. Мир арифметики
Задача предельного типа. Мир арифметики Презентация на тему Развивающие задачи для 5-6 классов
Презентация на тему Развивающие задачи для 5-6 классов  Переместительное свойство умножения
Переместительное свойство умножения Свойства умножения. 5 класс
Свойства умножения. 5 класс Математический турнир Умники и умницы
Математический турнир Умники и умницы Исследование операций. Принятие решений и неопределенность. Лекция 3
Исследование операций. Принятие решений и неопределенность. Лекция 3 11 клас призма
11 клас призма Метод Гаусса решения систем линейных уравнений
Метод Гаусса решения систем линейных уравнений Площадь треугольника
Площадь треугольника Параллельные прямые
Параллельные прямые Презентация на тему Построение точек по заданным координатам
Презентация на тему Построение точек по заданным координатам  Как может математика помочь быть здоровым?
Как может математика помочь быть здоровым? Состав чисел в приделах 10. Закрепление изученного материала
Состав чисел в приделах 10. Закрепление изученного материала Корень n-ой степени
Корень n-ой степени Шестое математическое действие
Шестое математическое действие Подготовка к ЕГЭ. Тестирование
Подготовка к ЕГЭ. Тестирование