Реляционная алгебра

Содержание
Необходимые определения
Операции реляционной алгебры
Объединение
Задание
Примеры
Пересечение
Разность
Произведение
Селекция
Проекция
Контрольные вопросы
Список литературы
Деление
Соединение

Необходимые определения
Отношение – это двумерная таблица, содержащая некоторые данные, для которой выполняются следующие условия:
В таблице не может быть одинаковых строк.
Имена столбцов должны быть различны.
Порядок строк в таблице может быть произвольным.
Все строки в таблице должны иметь одинаковую структуру.
Схема отношения – список атрибутов этого отношения.
Совместимые по объединению отношения – это отношения, имеющие одно и то же множество имен атрибутов.

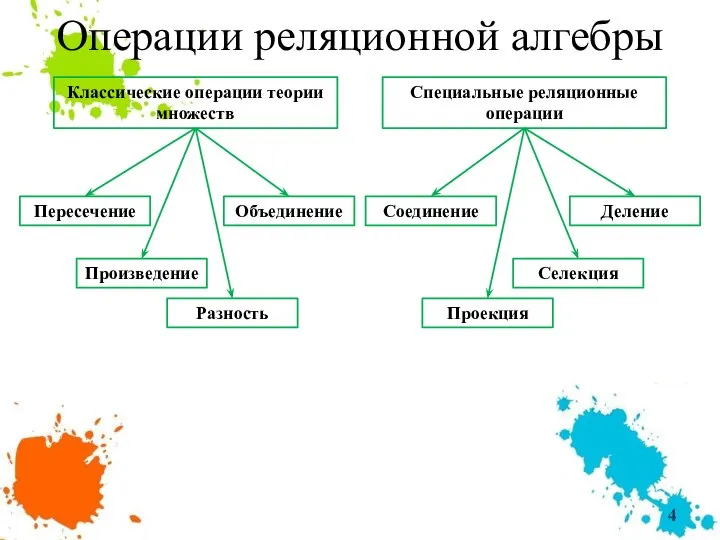
Операции реляционной алгебры
Классические операции теории множеств
Специальные реляционные операции
Объединение
Разность
Пересечение
Произведение
Проекция
Селекция
Деление
Соединение

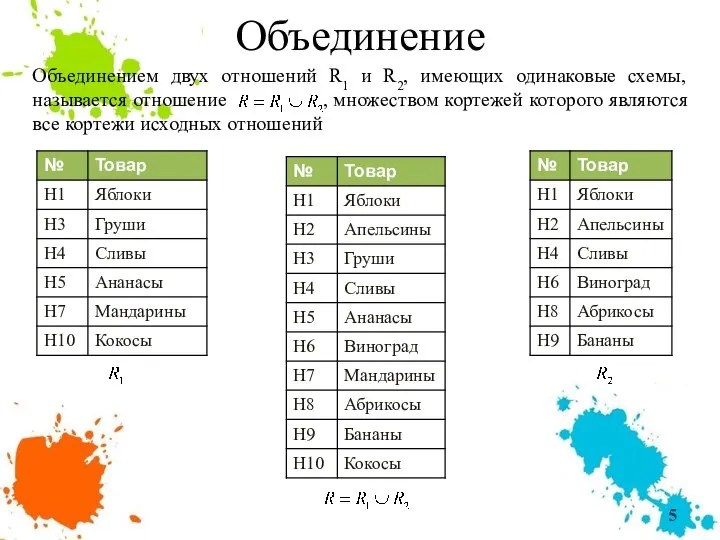
Объединение
Объединением двух отношений R1 и R2, имеющих одинаковые схемы, называется отношение , множеством кортежей которого являются все кортежи исходных отношений

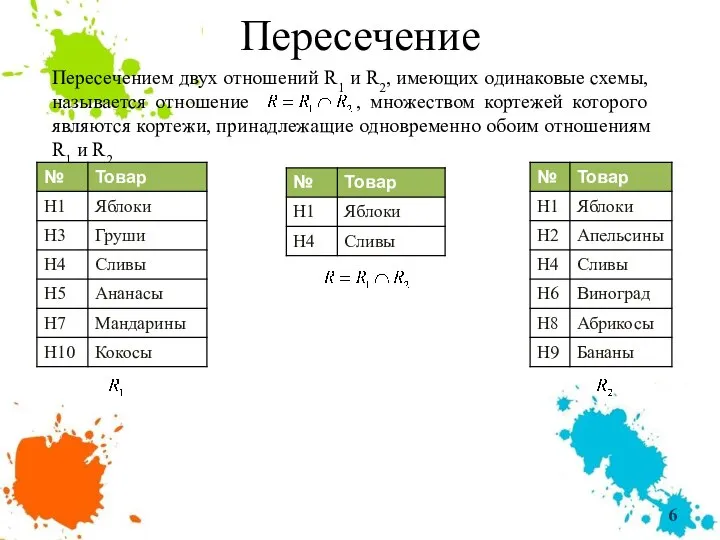
Пересечение
Пересечением двух отношений R1 и R2, имеющих одинаковые схемы, называется отношение , множеством кортежей которого являются кортежи, принадлежащие одновременно обоим отношениям R1 и R2

Разность
Разностью двух отношений R1 и R2, имеющих одинаковые схемы, называется отношение , множеством кортежей которого являются кортежи, принадлежащие первому отношению R1 и не принадлежащие второму отношению R2

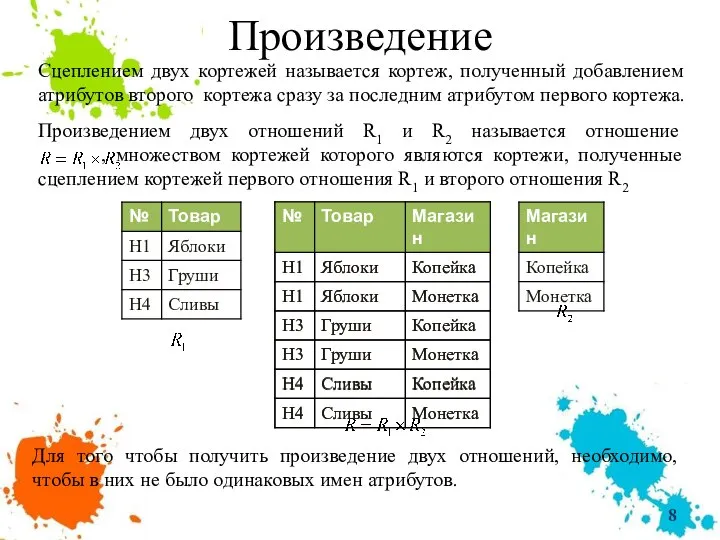
Произведение
Сцеплением двух кортежей называется кортеж, полученный добавлением атрибутов второго кортежа сразу за последним атрибутом первого кортежа.
Произведением двух отношений R1 и R2 называется отношение , множеством кортежей которого являются кортежи, полученные сцеплением кортежей первого отношения R1 и второго отношения R2
Для того чтобы получить произведение двух отношений, необходимо, чтобы в них не было одинаковых имен атрибутов.

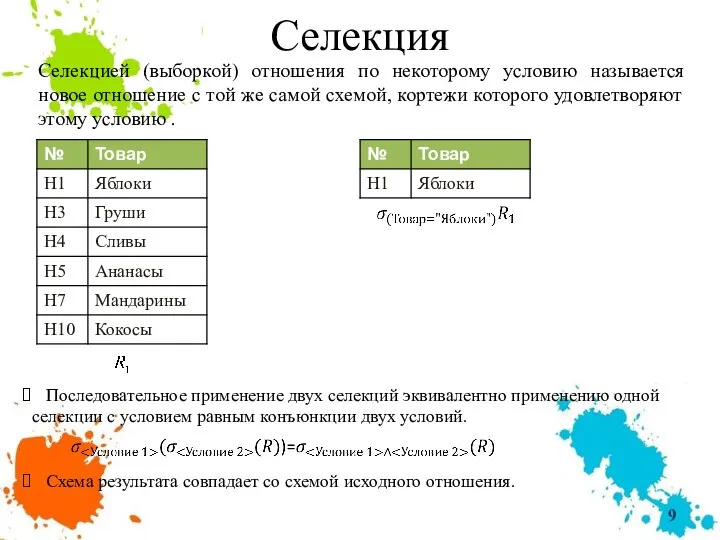
Селекция
Селекцией (выборкой) отношения по некоторому условию называется новое отношение с той же самой схемой, кортежи которого удовлетворяют этому условию .
Последовательное применение двух селекций эквивалентно применению одной селекции с условием равным конъюнкции двух условий.
Схема результата совпадает со схемой исходного отношения.

Проекция
Проекцией отношения на подмножество его атрибутов называется отношение, содержащее эти атрибуты и все кортежи исходного отношения, в которых содержатся значения данных атрибутов.

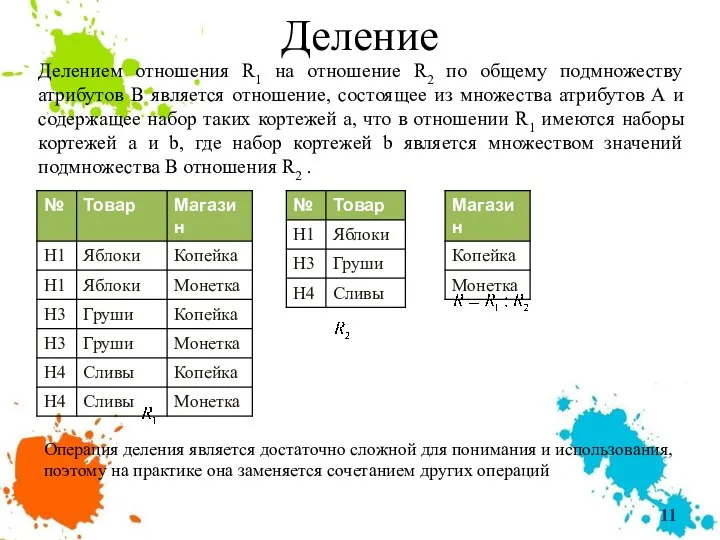
Деление
Делением отношения R1 на отношение R2 по общему подмножеству атрибутов В является отношение, состоящее из множества атрибутов А и содержащее набор таких кортежей а, что в отношении R1 имеются наборы кортежей а и b, где набор кортежей b является множеством значений подмножества В отношения R2 .
Операция деления является достаточно сложной для понимания и использования, поэтому на практике она заменяется сочетанием других операций

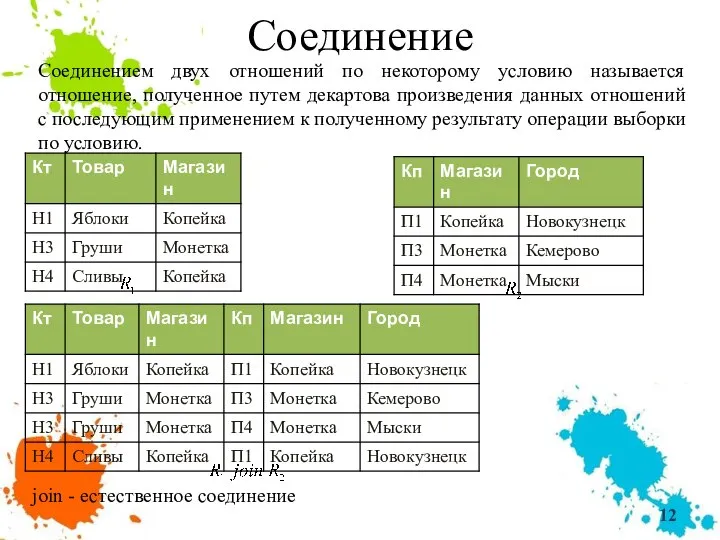
Соединение
Соединением двух отношений по некоторому условию называется отношение, полученное путем декартова произведения данных отношений с последующим применением к полученному результату операции выборки по условию.
join - естественное соединение

Примеры
4. Выдать ФИО студентов с указанием их групп.
1. Выдать ФИО студентов, родившихся до 1 сентября 1996 года.
2. Выдать ФИО студентов, не получающих стипендию.
3. Сформировать список студентов – мужчин, получающих стипендию.

Примеры
5. Получить список студентов, которые в январе сдали на оценку «отлично» как минимум один экзамен
6. Получить список студентов, которые сдали математику и физику на оценку «отлично»
7. Получить список кафедр, преподаватели которых поставили как минимум одну оценку «неудовлетворительно»

Задание
Получить названия животных, средняя продолжительность жизни которых меньше 15 лет.
Получить названия зоопарков, у которых нет сайта.
Получить список животных, которые либо кенгуру, либо живут в среднем меньше 5 лет.
Получить список животных с указанием классов.
Получить список животных, обитающих в Московском зоопарке, с указанием количества экземпляров.
Получить список животных, питающихся фруктами или злаками.
Получить список продуктов, которыми кормят дельфинов в Московском зоопарке.
Получить список зоопарков, где альбатросов кормят мелкими беспозвоночными.

Контрольные вопросы
Что такое «Отношение»?
Перечислите операции реляционной алгебры.
Что получится в результате выполнения операции объединения, пересечения, разности? Приведите примеры. Сформулируйте условие, предъявляемое к схемам отношений, для возможности выполнения данных операций.
Что получится в результате выполнения операции произведения? Приведите пример. Сформулируйте условие, предъявляемое к отношениям, для возможности выполнения данной операции.