Элементы теории графов

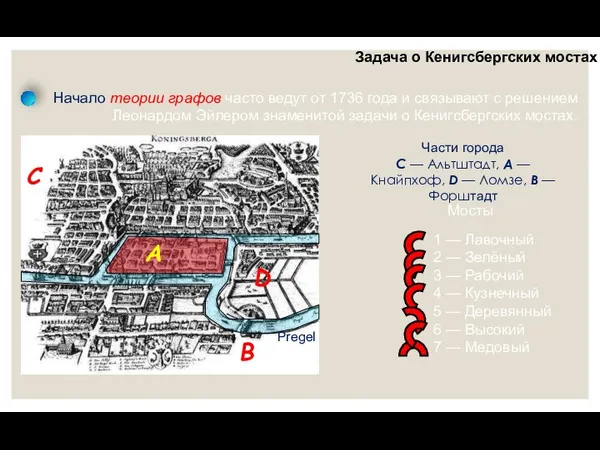
Задача о Кенигсбергских мостах
Начало теории графов часто ведут от 1736 года и связывают с решением Леонардом Эйлером знаменитой задачи о Кенигсбергских мостах.
1 — Лавочный
2 — Зелёный
3 — Рабочий
4 — Кузнечный
5 — Деревянный
6 — Высокий
7 — Медовый
C
Части города
C — Альтштадт, A — Кнайпхоф, D — Ломзе, B — Форштадт
A
D
B
Мосты
Pregel

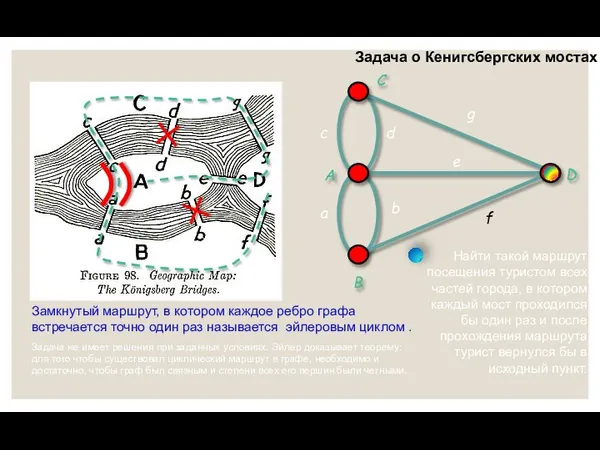
Задача о Кенигсбергских мостах
Задача не имеет решения при заданных условиях. Эйлер доказывает теорему: для того чтобы существовал циклический маршрут в графе, необходимо и достаточно, чтобы граф был связным и степени всех его вершин были четными.
a
b
c
d
g
f
e
Замкнутый маршрут, в котором каждое ребро графа встречается точно один раз называется эйлеровым циклом .
Найти такой маршрут посещения туристом всех частей города, в котором каждый мост проходился бы один раз и после прохождения маршрута турист вернулся бы в исходный пункт.

Основные определения
В наиболее общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами : G = { V, E } ,
где V есть множество вершин, а E - подмножество V × V , называемое множеством ребер, если пары неупорядочены, и множеством дуг, если пары упорядочены.
Теория графов – раздел дискретной математики, изучающей свойства графов. В математической теории графов и информатике граф — это совокупность объектов со связями между ними. Определение ввел венгерский математик Д. Кёниг в 1936 г.
В первом случае граф G = { V, E } называется неориентированным, во втором – ориентированным – (орграфом).

Основные определения
Теория графов находит применение, например, в геоинформационных системах (ГИС). Дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередач и т. п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь, спланировать оптимальный маршрут.
Теория графов не обладает устоявшейся терминологией. Под одними и теми же терминами понимаются разные вещи.
Элементы множества V называются вершинами графа, элементы множества E – его ребрами (дугами).

Основные определения
Если e = ( v1, v2 ) , и e включено в E , то говорят что ребро e – соединяет вершины (v1, v2 ) , если v1 =v2, то ребро e называется петлей. Две вершины v1 ,v2 называются смежными, если существует соединяющее их ребро. Аналогично два различных ребра - смежные, если они имеют общую вершину.
Степенью вершины v называется число ребер d (v) , инцидентных ей, при этом петля учитывается дважды. В случае ориентированого графа различают степень do (v) по выходящим дугам и di (v) – по входящим.
Графы могут не нумероваться, быть пронумерованными по вершинам, по ребрам. Есть цветные графы (по ребрам, вершинам, и по ребрам и по вершинам).

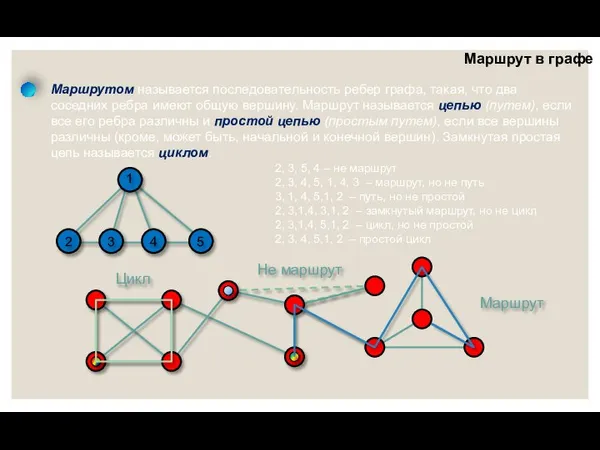
Маршрут в графе
Маршрутом называется последовательность ребер графа, такая, что два соседних ребра имеют общую вершину. Маршрут называется цепью (путем), если все его ребра различны и простой цепью (простым путем), если все вершины различны (кроме, может быть, начальной и конечной вершин). Замкнутая простая цепь называется циклом.
1
2
3
4
5
2, 3, 5, 4 – не маршрут
2, 3, 4, 5, 1, 4, 3 – маршрут, но не путь
3, 1, 4, 5,1, 2 – путь, но не простой
2, 3,1,4, 5,1, 2 – цикл, но не простой
2, 3, 4, 5,1, 2 – простой цикл
2, 3,1,4, 3,1, 2 – замкнутый маршрут, но не цикл
Не маршрут
Маршрут
Цикл

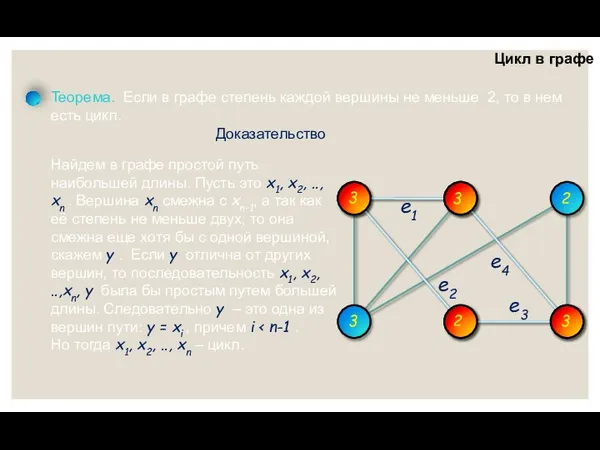
Цикл в графе
Теорема. Если в графе степень каждой вершины не меньше 2, то в нем есть цикл.
Найдем в графе простой путь наибольшей длины. Пусть это x1, x2, .., xn . Вершина xn смежна с xn-1, а так как её степень не меньше двух, то она смежна еще хотя бы c одной вершиной, скажем y . Если y отлична от других вершин, то последовательность x1, x2, ..,xn, y была бы простым путем большей длины. Следовательно y – это одна из вершин пути: y = xi , причем i < n-1 .
Но тогда x1, x2, .., xn – цикл.
Доказательство
3
3
3
3
2
2

Число графов
Доказательство

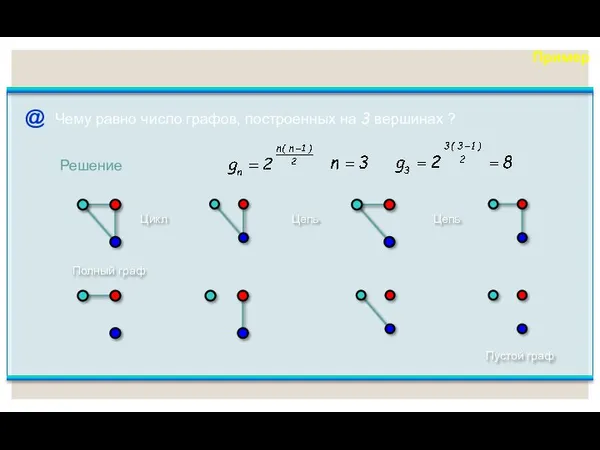
Пример
Чему равно число графов, построенных на 3 вершинах ?
Цикл
Полный граф
Пустой граф
Цепь
Цепь
@
Решение

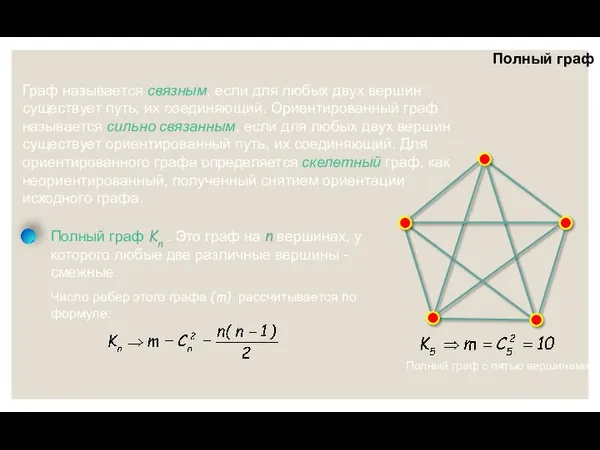
Полный граф
Граф называется связным, если для любых двух вершин существует путь, их соединяющий. Ориентированный граф называется сильно связанным, если для любых двух вершин существует ориентированный путь, их соединяющий. Для ориентированного графа определяется скелетный граф, как неориентированный, полученный снятием ориентации исходного графа.
Полный граф Kn . Это граф на n вершинах, у которого любые две различные вершины - смежные.
Полный граф с пятью вершинами
Число ребер этого графа (m) рассчитывается по формуле:

Смежность, инцидентность, степени
Множество всех вершин графа, смежных с данной вершиной а , называется окрестностью этой вершины и обозначается через V(a) .
Это равенство известно как «лемма о рукопожатиях». Из него следует, что число вершин нечетной степени в любом графе четно.

Смежность, инцидентность, степени
Лемма (о рукопожатиях). Любой граф содержит четное число вершин нечетной степени.
Если граф G имеет xi вершин степени i, то: x1 + 2x2 +…+ kxk = 2|E| ,
поскольку мы подсчитываем число концевых вершин ребер, а каждое ребро имеет точно две концевые вершины. Отсюда получаем, что сумма вершин с нечетной степенью x2i+1 есть четное число.
Доказательство
Вершину степени 0 называют изолированной. Граф называют регулярным степени d, если степень каждой его вершины равна d .
Набор степеней графа – это последовательность степеней его вершин, выписанных в неубывающем порядке.
2e(G) = 2*4 = 8

Матрицы и графы
Пусть дан граф G (V, E ) , построенных на n вершинах. Для него можно построить матрицу смежности Aij вершин
( элемент Aij : 1 - две вершины связаны одним ребром, 0 - не связаны )

Матрицы и графы
Другая матрица, ассоциированная с графом G (V, E ) – матрица инцидентности . Для её построения вершины (строки) нумеруются от 1 до n , а ребра (столбцы) от 1 до m . Её элементы равны единице, если вершина i инцидентна ребру j , в противном случае они равны нулю. Если граф ориентированный, то направление его дуг учитывают знаком. Если есть петли, ставят какой любой знак.
Для ориентированного графа матрица инцидентности определяется несколько иначе: ее элемент равен 1, если вершина i является началом ребра j , элемент равен -1, если вершина является концом этого ребра, элемент равен 0, если эта вершина и это ребро не инцидентны друг другу.