Повторение курса алгебры за 10 класс

Разделы 2 полугодия
Раздел 10.3A: Многочлены
Раздел 10.3B: Предел функции и непрерывность
Раздел 10.3C: Производная
Раздел 10.4A: Применение производной
Раздел 10.4B: Случайные величины и их числовые характеристики

Цель урока
Повторить разделы:
Многочлены.
Предел функции и непрерывность.
Производная.
Применение производной.
Случайные величины и их числовые характеристики.
Вероятность.

Теорема Безу
Теорема: Остаток многочлена при деление на двучлен x-a равен значению многочлена в точке x=a.

Рассмотрим многочлен
где a1, a2, ..., an − целые числа, an ≠ 0.
Теорема о рациональных корнях многочлена

1. Используя схему Горнера разделите многочлен f (x) на бином
1) f(x) = x4 - 2x3 + 4x2 - 6x + 8, = 1
f(x)= (x-1)(x3 – x2 + 3x – 3)+ 5

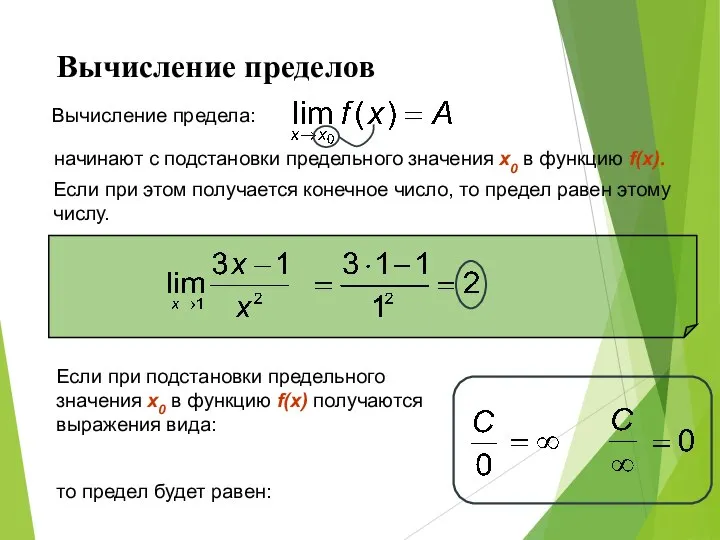
Вычисление пределов
Вычисление предела:
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому числу.
Если при подстановки предельного значения x0 в функцию f(x) получаются выражения вида:
то предел будет равен:

Вычисление пределов
Часто при подстановке предельного значения x0 в функцию f(x) получаются выражения следующих видов:
Эти выражения называются неопределенности, а вычисление пределов в этом случае называется раскрытие неопределенности.

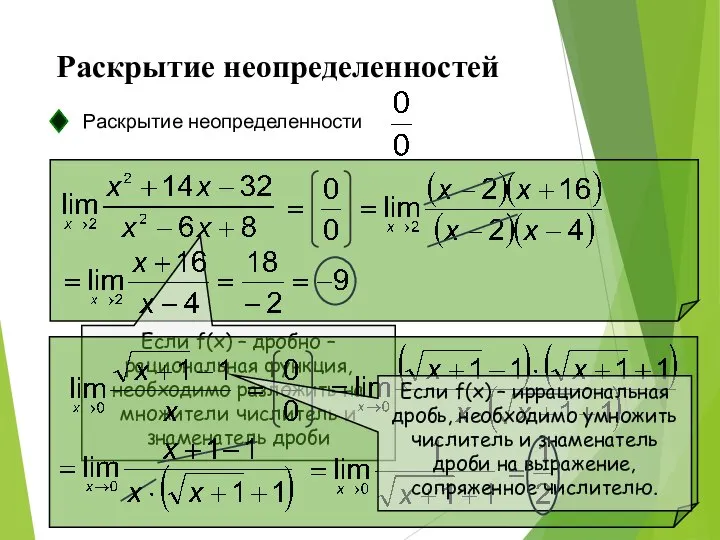
Раскрытие неопределенностей
Раскрытие неопределенности
Если f(x) – дробно – рациональная функция, необходимо разложить на множители числитель и знаменатель дроби
Если f(x) – иррациональная дробь, необходимо умножить числитель и знаменатель дроби на выражение, сопряженное числителю.

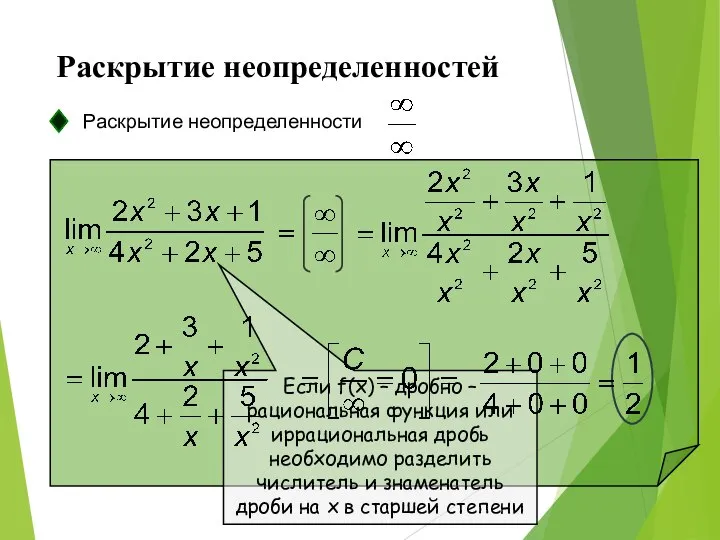
Раскрытие неопределенностей
Раскрытие неопределенности
Если f(x) – дробно – рациональная функция или иррациональная дробь необходимо разделить числитель и знаменатель дроби на x в старшей степени

ТАБЛИЦА
ПРОИЗВОДНЫХ
ПРАВИЛА ВЫЧИСЛЕНИЯ
ПРОИЗВОДНЫХ

ТАБЛИЦА ПРОИЗВОДНЫХ

Исследование функции
1) Область определения функции
2) Свойства функции (четность, нечетность, периодичность)
4) Точки пересечения функции с осями координат
5) Непрерывность функции. Характер точек разрыва
6) Асимптоты
7) Экстремумы функции. Исследование функции на монотонность
8) Выпуклость/вогнутость графика функции. Точки перегиба

Исследуем функцию и построим её график
1) Поскольку знаменатель положителен при всех , область определения функции - вся ось
2) Функция f(x) - нечётная, поскольку при смене знака x числитель меняет знак, а знаменатель остаётся без изменения, откуда f(-x) = - f(x). Следовательно, график функции симметричен относительно начала координат.
Периодической функция не является.
3) Поскольку область определения этой элементарной функции - вся вещественная ось, вертикальных асимптот график не имеет.

4) Найдём наклонные асимптоты при в виде . Имеем:
Таким образом, асимптотой как при , так и при служит прямая

5) Найдём точки пересечения с осями координат. Имеем:
f(0) = 0, причём x=0 - единственное решение уравнения f(x) = 0. Значит, график y = f(x) пересекает сразу и ось Ox, и ось Oy в начале координат.
Очевидно, что f(x)>0 при x>0 и f(x)<0 при x<0.

6) Найдём производную:
Очевидно, что f´(x) ≥ 0 при всех ; единственная точка, в которой f´(x) = 0 - это x=0. Значит, функция f(x) возрастает на всей оси Ox, а в стационарной точке x=0 имеет горизонтальную касательную.

7) Найдём вторую производную:
Знаменатель этой дроби положителен при всех x. Числитель имеет корни x=0 и x=±√3, при этом f’’(x)>0 на интервалах и - на этих интервалах функция выпукла. На интервалах и выполняется обратное неравенство f’’(x)<0, здесь функция вогнута. Все три точки, в которых f’’(x)=0, то есть точки - √3, 0, √3, являются точками перегиба.

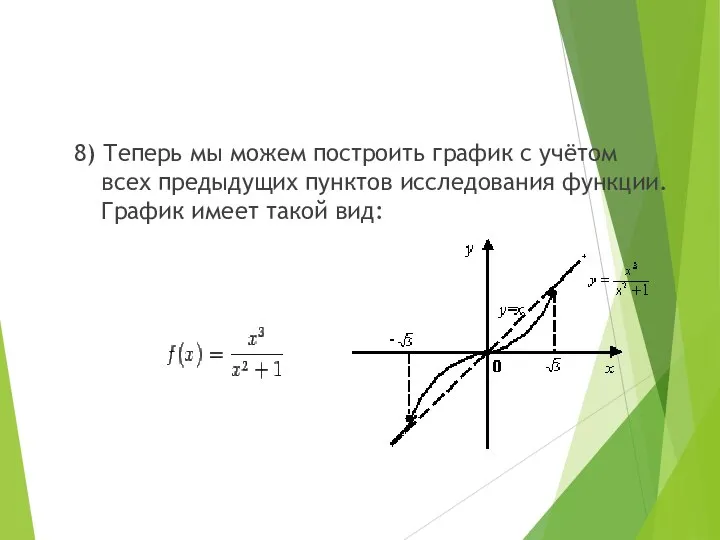
8) Теперь мы можем построить график с учётом всех предыдущих пунктов исследования функции. График имеет такой вид:

Пример: Партия из 10 телевизоров содержит четыре исправных телевизора. Из этой партии наугад выбирают три телевизора. Составить закон распределения числа неисправных телевизоров в выборке
Решение: Из 10 телевизоров выбираем любые 3: это все равновозможные исходы. Вероятность р(А) = 1/120