Содержание
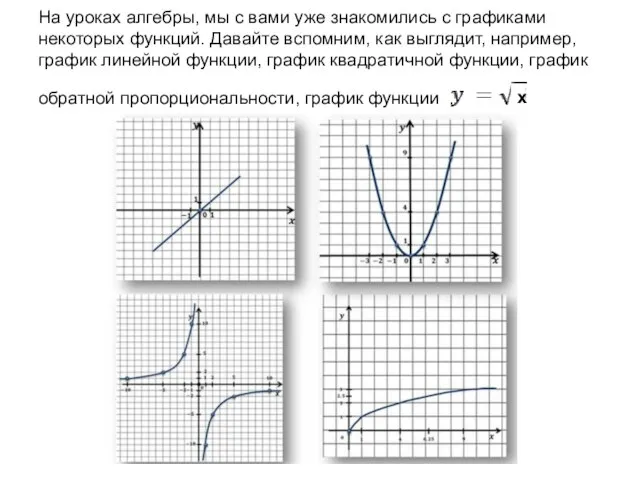
- 2. На уроках алгебры, мы с вами уже знакомились с графиками некоторых функций. Давайте вспомним, как выглядит,
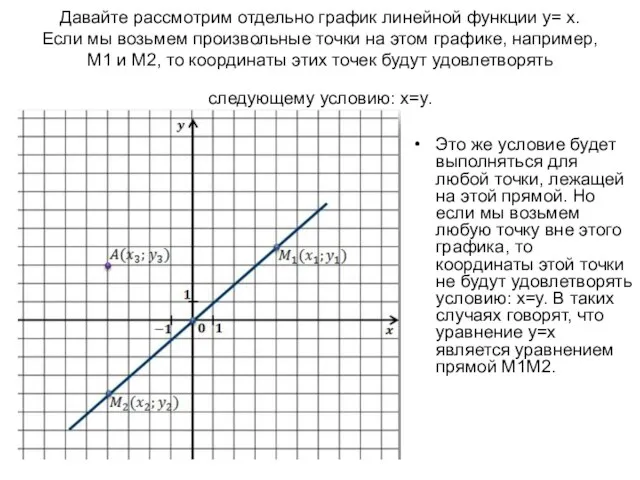
- 3. Давайте рассмотрим отдельно график линейной функции y= x. Если мы возьмем произвольные точки на этом графике,
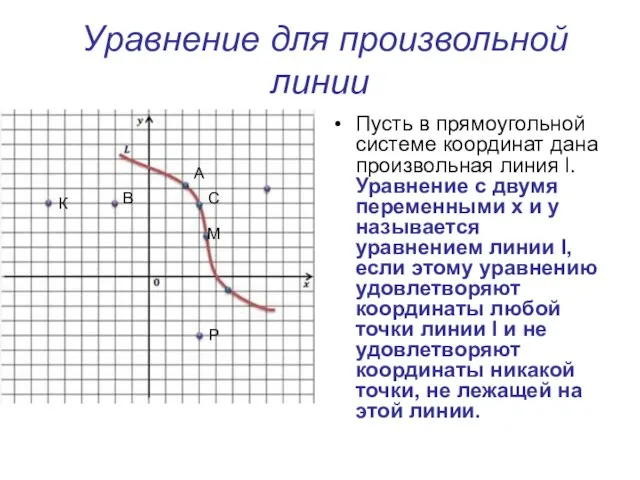
- 4. Уравнение для произвольной линии Пусть в прямоугольной системе координат дана произвольная линия l. Уравнение с двумя
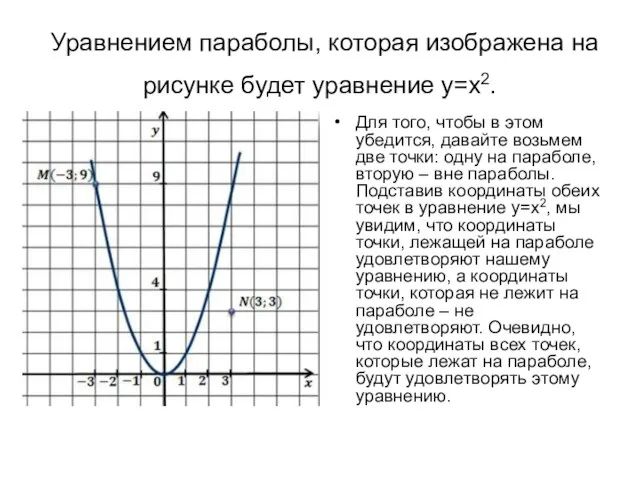
- 5. Уравнением параболы, которая изображена на рисунке будет уравнение y=x2. Для того, чтобы в этом убедится, давайте
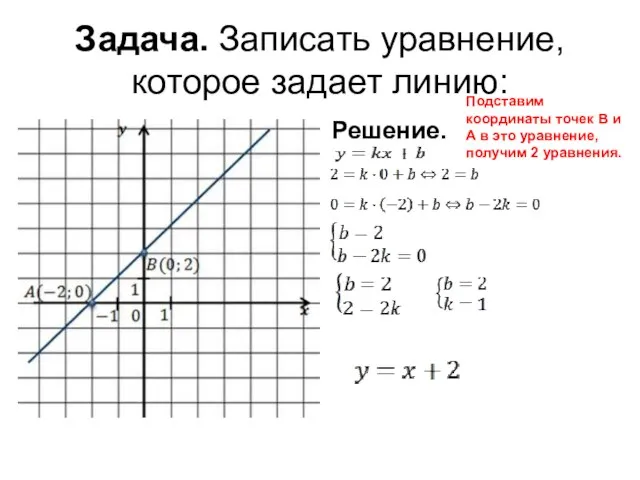
- 6. Задача. Записать уравнение, которое задает линию: Решение. Подставим координаты точек В и А в это уравнение,
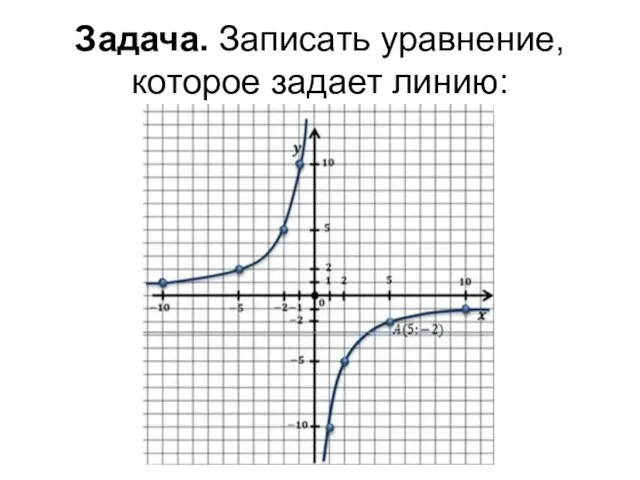
- 7. Задача. Записать уравнение, которое задает линию:
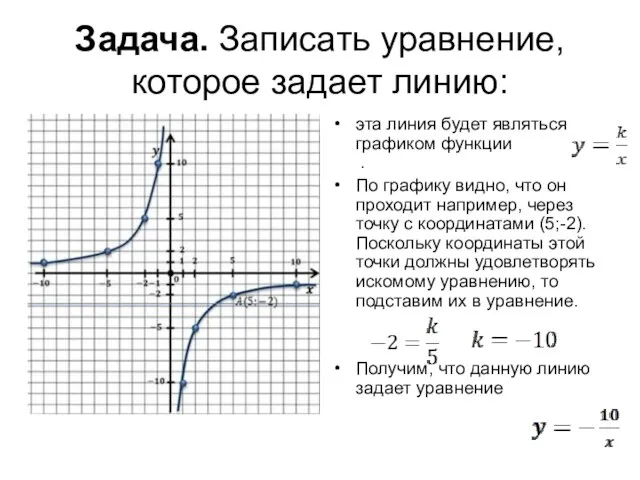
- 8. Задача. Записать уравнение, которое задает линию: эта линия будет являться графиком функции . По графику видно,
- 9. 09.11. Тема урока: Уравнение окружности В тетрадь запиши все, что обозначено зеленой галочкой.
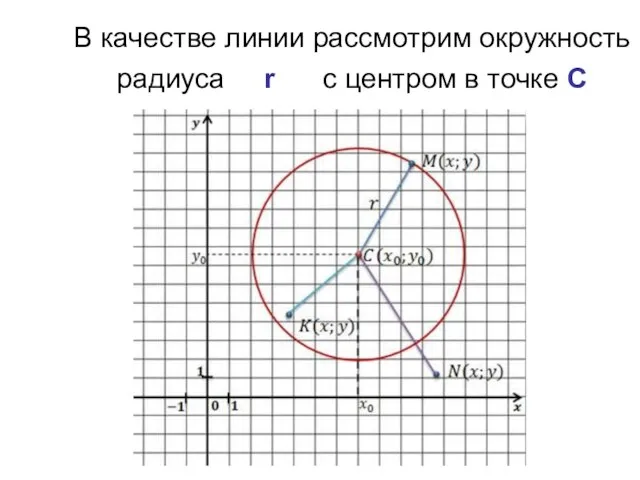
- 10. В качестве линии рассмотрим окружность радиуса r с центром в точке С
- 11. В качестве линии рассмотрим окружность радиуса r с центром в точке С Пусть центр окружности имеет
- 12. Мы знаем, что длина отрезка, который соединяет любую точку на окружности с центром окружности – это
- 13. Получим, что если точка лежит на окружности с радиусом r и центром в точке C, то
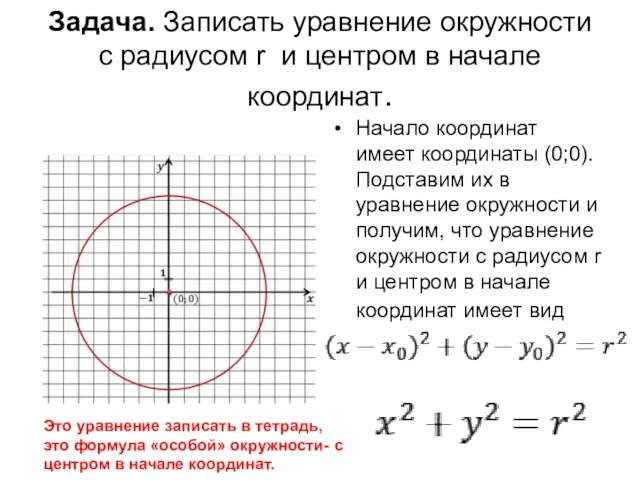
- 14. Задача. Записать уравнение окружности с радиусом r и центром в начале координат. Начало координат имеет координаты
- 15. Являются ли данные уравнения, уравнениями окружности? x2 +(y+2)2 = 2 4x 2 + y 2 =
- 16. Проанализируй таблицу на следующем слайде. Твоя задача- разобраться как получаем координату центра окружности и длину радиуса.
- 17. (x–3)2 +(y–2)2 =16 (x–1)2+(y+2)2 = 4 (x+5)2+(y–3)2 = 25 (x – 1 )2 + y 2
- 18. Задача. Начертить окружность, заданную уравнением Прежде всего, определимся с координатами центра окружности. Это будут числа 5
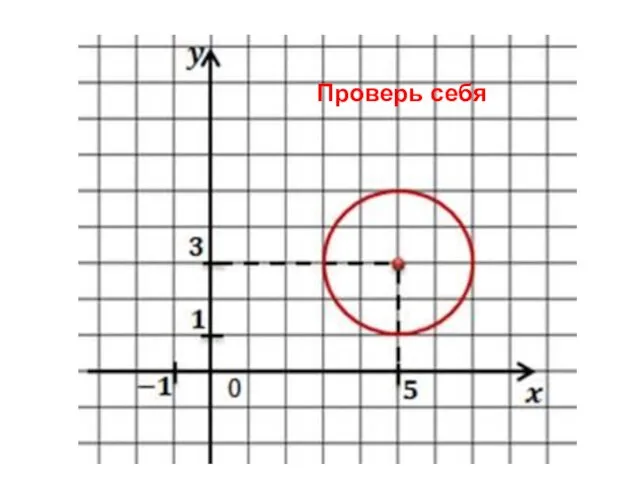
- 19. Проверь себя
- 20. Задача. Начертить окружность, заданную уравнением Это сделай самостоятельно.
- 21. 1 вариант 2 вариант Задание: выпишите координаты центра окружности и её радиус
- 23. Скачать презентацию










 Решение заданий ЕГЭ уровня С2 (1 часть)
Решение заданий ЕГЭ уровня С2 (1 часть) Сочетательное и распределительное свойство умножения. Урок 1
Сочетательное и распределительное свойство умножения. Урок 1 Признаки делимости на 2, 5,10, 3, 6 и 9
Признаки делимости на 2, 5,10, 3, 6 и 9 Параллельные прямые в пространстве
Параллельные прямые в пространстве Неопределенный интеграл
Неопределенный интеграл Урок 53. Расстояние от точки до прямой
Урок 53. Расстояние от точки до прямой Степень с рациональным показателем
Степень с рациональным показателем Косинус угла
Косинус угла Производная сложной функции
Производная сложной функции Понятие вектора
Понятие вектора Определители. Матрица и ее определитель
Определители. Матрица и ее определитель Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Задания на развитие логики
Задания на развитие логики 20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами
20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами Деловая игра Маркетинг инноваций
Деловая игра Маркетинг инноваций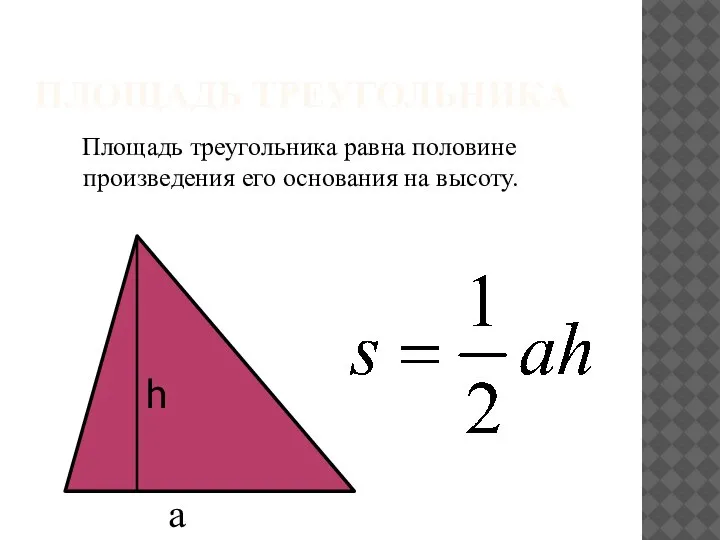 Площадь треугольника
Площадь треугольника Математика без границ. Конкурс
Математика без границ. Конкурс Сантиметр. Линейка
Сантиметр. Линейка Золотое сечение
Золотое сечение Информатика. Вероятность
Информатика. Вероятность Загадки и тайны треугольника
Загадки и тайны треугольника Сложение вида + 2, + 3
Сложение вида + 2, + 3 Презентация на тему Признаки равенства треугольников
Презентация на тему Признаки равенства треугольников  Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике)
Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике) Умножение одночлена на многочлен
Умножение одночлена на многочлен Современная финансовая математика
Современная финансовая математика Элементы круга и окружности в задачах ОГЭ
Элементы круга и окружности в задачах ОГЭ Плоскость и прямая в пространстве
Плоскость и прямая в пространстве