Правильные многогранники, полуправильные

ПРАВИЛЬНЫЙ МНОГОГРАННИК
Правильным многогранником называется выпуклый многогранник, грани которого – равные правильные многоугольники, а двугранные углы при всех вершинах равны между собой. Доказано, что в каждой из вершин правильного многогранника сходится одно и то же число граней и одно и то же число ребер.

ПЯТЬ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
Правильные многогранники имеют названия по числу граней: тетраэдр (4 грани): гексаэдр (6 граней), октаэдр (8 граней), додекаэдр (12 граней) и икосаэдр (20 граней). По-гречески "хедрон" означает грань, "тетра", "гекса" и т. д. – указанные числа граней. Нетрудно догадаться, что гексаэдр есть не что иное, как всем знакомый куб. Грани тетраэдра, октаэдра и икосаэдра – правильные треугольники, куба - квадраты, додекаэдра – правильные пятиугольники.

ПЯТЬ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
Если обозначить количество углов у одной грани правильного многогранника за q, а количество граней, сходящихся в одной вершине – за p, можно получить точные характеристики каждого правильного многогранника. Вот они (первое число – q, второе – p): (3;3), (3;4), (4;3), (3;5), (5;3).

ТРЕУГОЛЬНЫЙ МНОГОГРАННИК ИЗ БУМАГИ
Для того, чтобы понять, что такое модульное оригами, необходимо сначала разобраться с тем, что называют модулем.
Все довольно просто: модуль - это один из оригамных элементов. Некая частица, входящая в состав большой, общей детали или изделия.

ТРЕУГОЛЬНЫЙ МНОГОГРАННИК ИЗ БУМАГИ
Множество одинаковых модулей, собранных вместе, образуют ту или иную конструкцию. Таким образом, модульное оригами можно назвать конструктором из традиционных фигурок.

ТРЕУГОЛЬНЫЙ МНОГОГРАННИК ИЗ БУМАГИ
Например, из фигурок стаканчиков можно выполнить мяч, кактус, цыпленка или петушка, простенький бумеранг и некоторые виды орнаментов. А из звездочек-сюрикенов - занимательную черепашку или огромный замок.

ТРЕУГОЛЬНЫЙ МНОГОГРАННИК ИЗ БУМАГИ
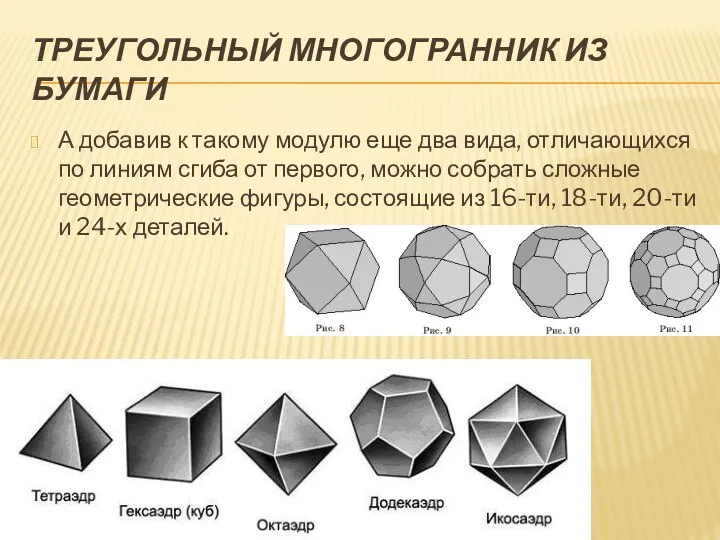
А добавив к такому модулю еще два вида, отличающихся по линиям сгиба от первого, можно собрать сложные геометрические фигуры, состоящие из 16-ти, 18-ти, 20-ти и 24-х деталей.