Преобразование графиков функций. 9 класс

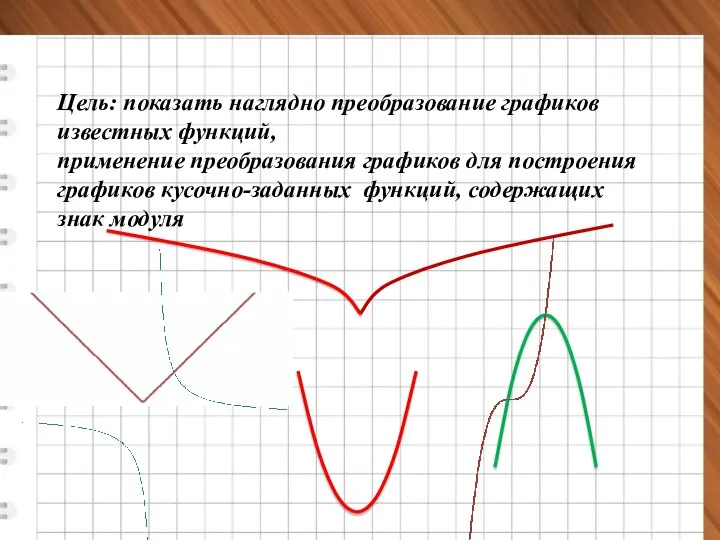
Цель: показать наглядно преобразование графиков
известных функций,
применение преобразования графиков для построения графиков кусочно-заданных функций, содержащих знак модуля

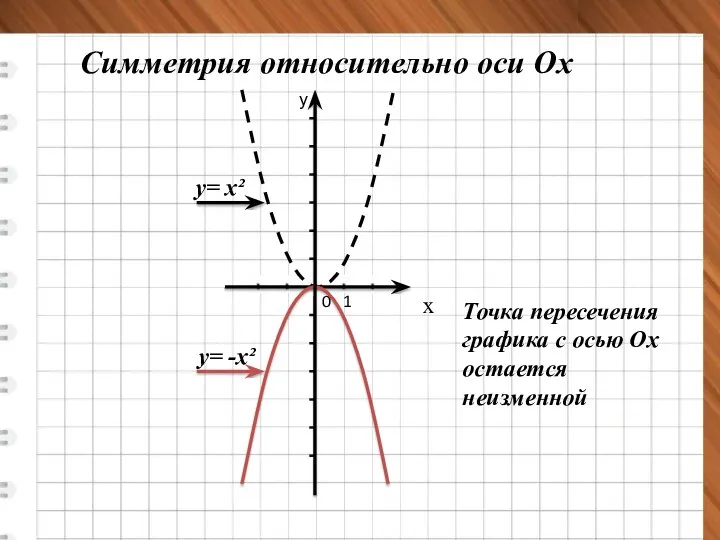
х
у
0 1
у= х²
у= -х²
Симметрия относительно оси Ох
Точка пересечения графика с осью Ох остается неизменной

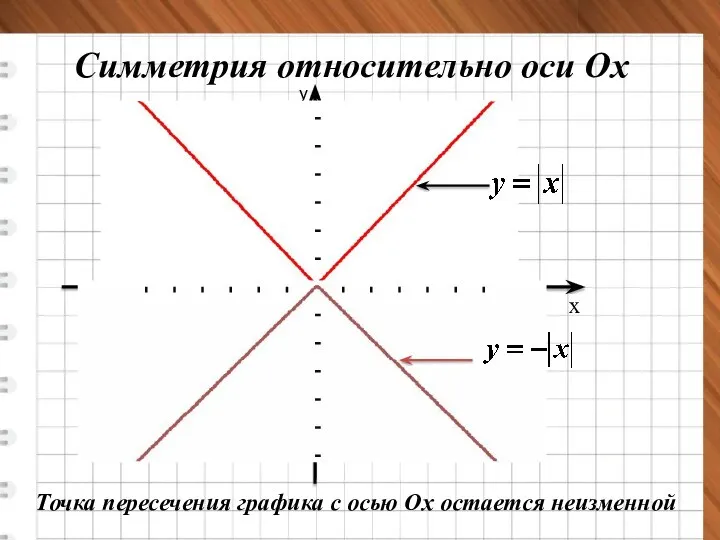
х
у
0 1
Симметрия относительно оси Ох
Точка пересечения графика с осью Ох остается неизменной

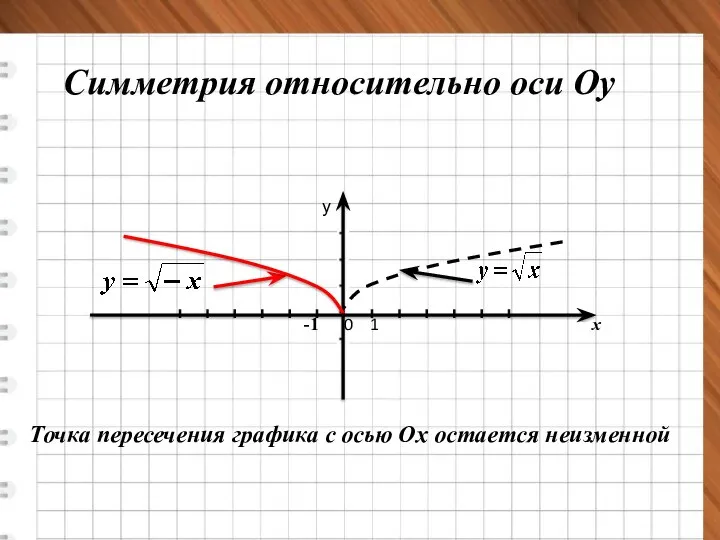
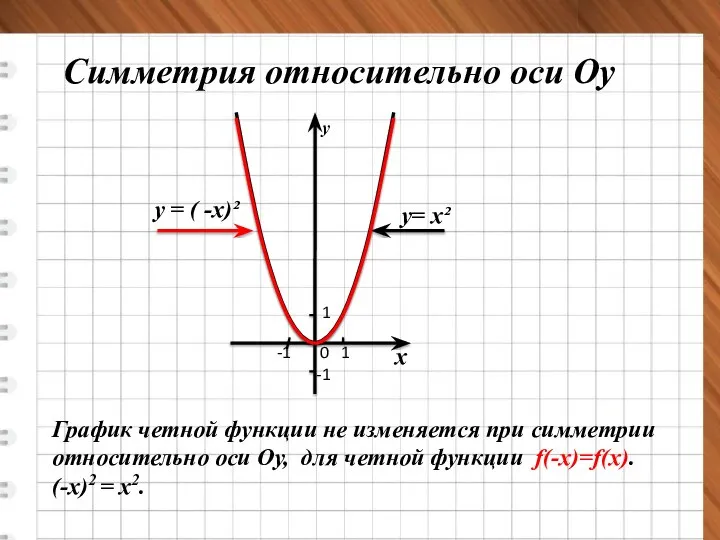
у= х²
у= -х²
х
у
0 1
-1
Симметрия относительно оси Оу
х
у
0 1
Точка пересечения графика с осью Ох остается неизменной

х
у
у = ( -х)²
у= х²
Симметрия относительно оси Оу
График четной функции не изменяется при симметрии относительно оси Оу, для четной функции f(-x)=f(x).
(-x)2 = x2.
0 1
-1
1
-1

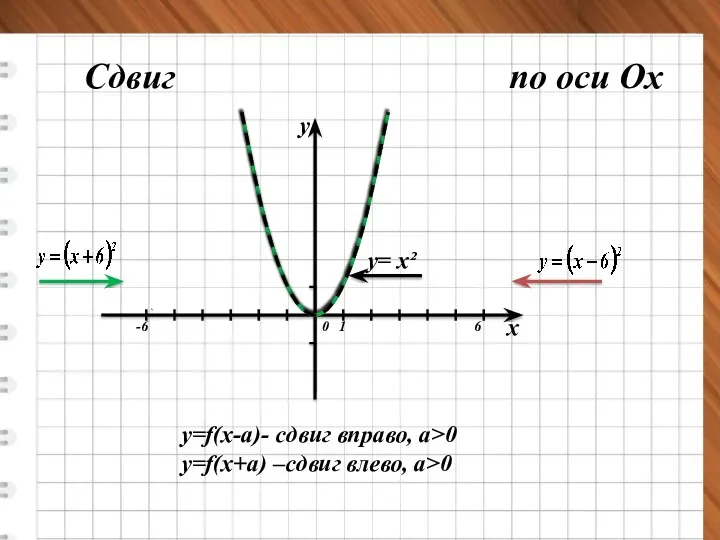
х
у
0 1
у= х²
6
-6
Сдвиг по оси Ох
y=f(x-a)- сдвиг вправо, a>0
y=f(x+a) –сдвиг влево, a>0

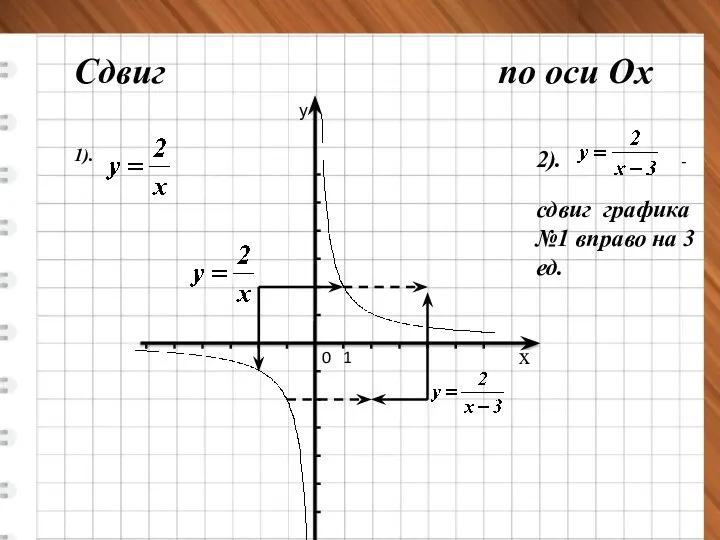
х
у
0 1
Сдвиг по оси Ох
1).
2). -
сдвиг графика №1 вправо на 3 ед.

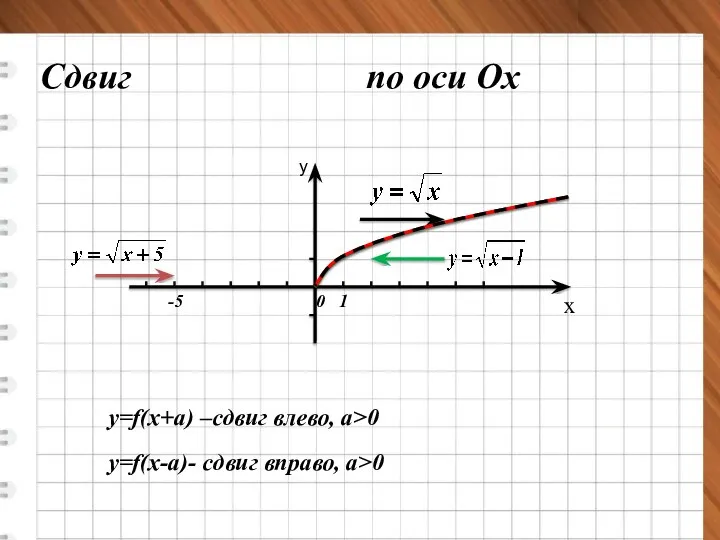
х
у
Сдвиг по оси Ох
y=f(x+a) –сдвиг влево, a>0
-5
y=f(x-a)- сдвиг вправо, a>0
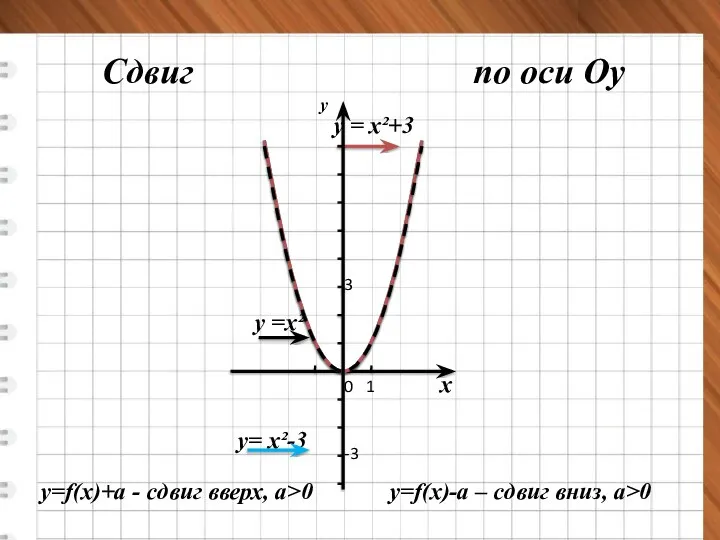
0 1

х
у
0 1
у = х²+3
у= х²-3
у =х²
Сдвиг по оси Оу
3
-3
y=f(x)+а - сдвиг вверх, a>0
y=f(x)-а – сдвиг вниз, a>0

х
у
0 1
1
2
3
4
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
2
3
4
5
Сдвиг по оси Оу
1).
2). -
сдвиг графика №1 вниз вдоль оси Оу на 2 ед.

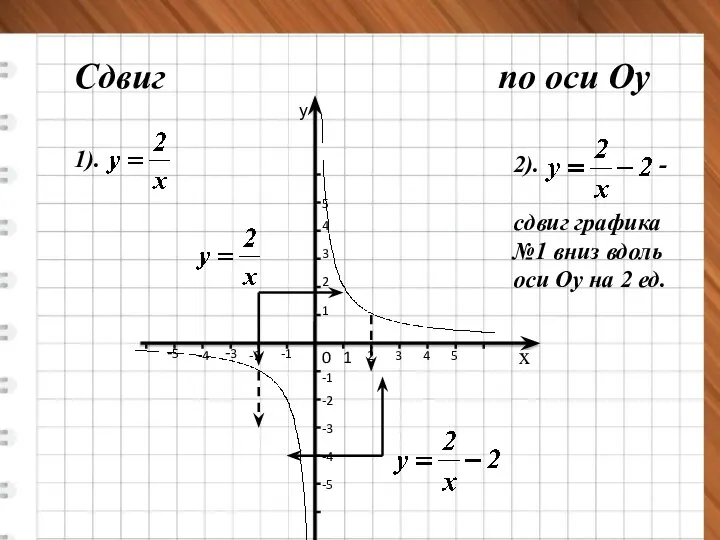
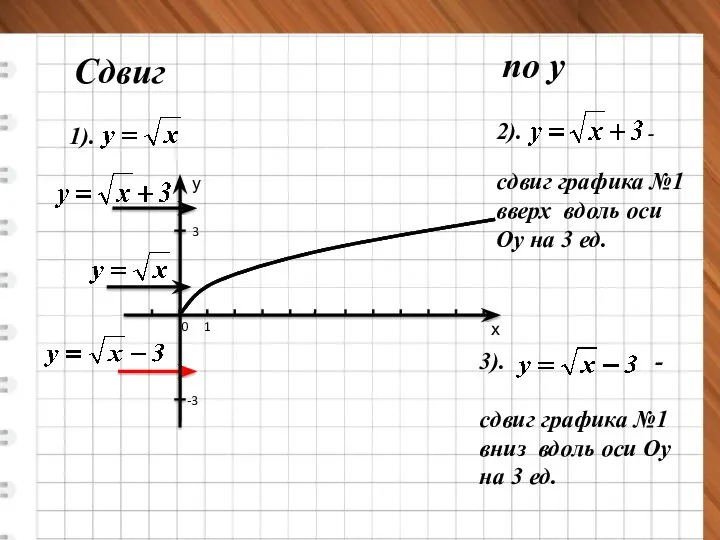
Сдвиг
по у
-3
3
0 1
х
у
2). -
сдвиг графика №1 вверх вдоль оси Оу на 3 ед.
1).
3). -
сдвиг графика №1 вниз вдоль оси Оу на 3 ед.

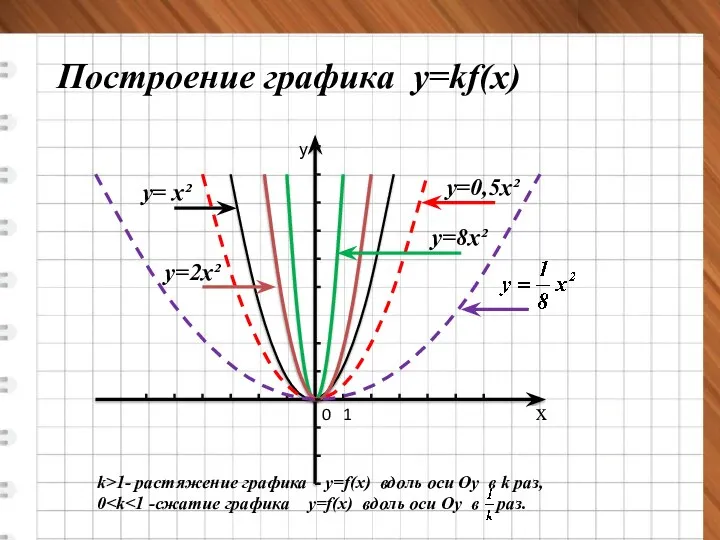
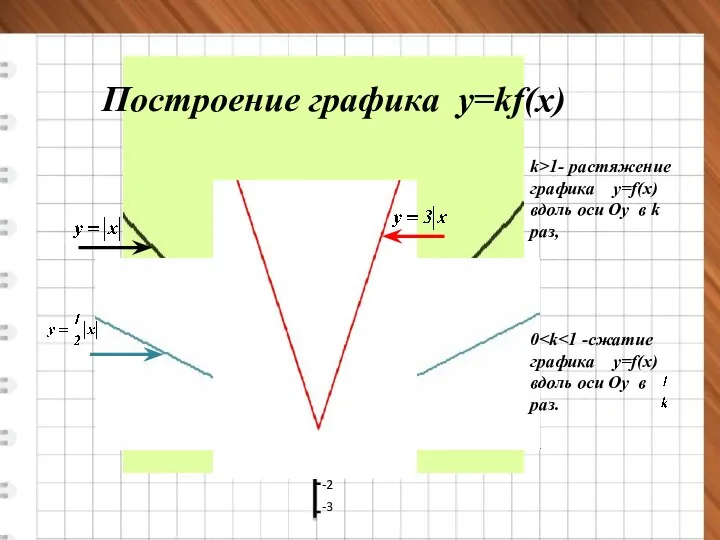
у= х²
у=2х²
х
у
0 1
у=8х²
у=0,5х²
Построение графика у=kf(x)
k>1- растяжение графика у=f(x) вдоль оси Оу в k раз,
0

х
у
2
4
5
6
7
8
1
0 1
-1
-2
-1
-2
-3
-4
-5
3
3
4
5
6
-3
2
Построение графика у=kf(x)
k>1- растяжение графика у=f(x) вдоль оси Оу в k раз,
0

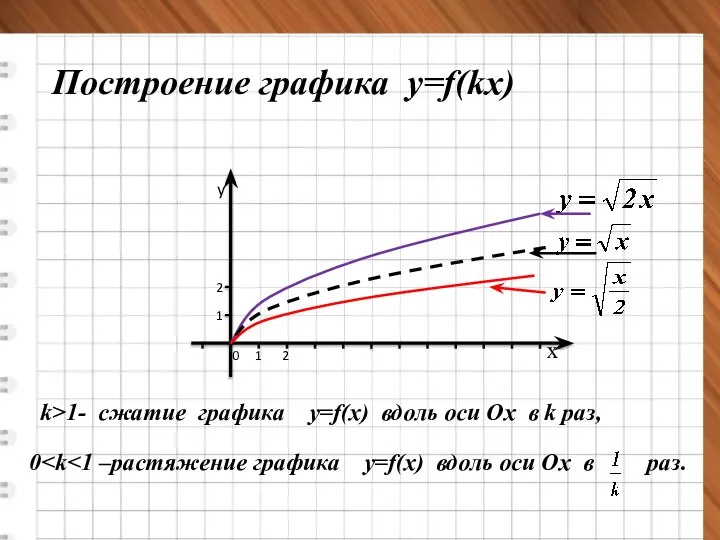
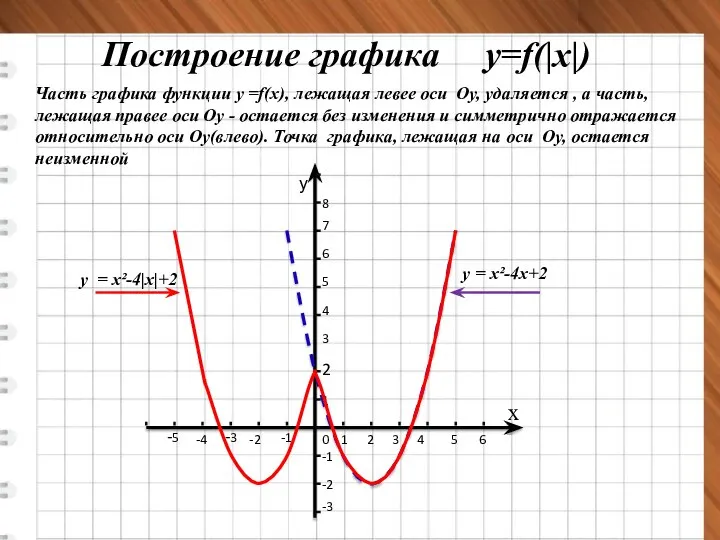
х
Построение графика у=f(kx)
0 1
2
1
2
y
k>1- cжатие графика у=f(x) вдоль оси Ох в k раз,
0

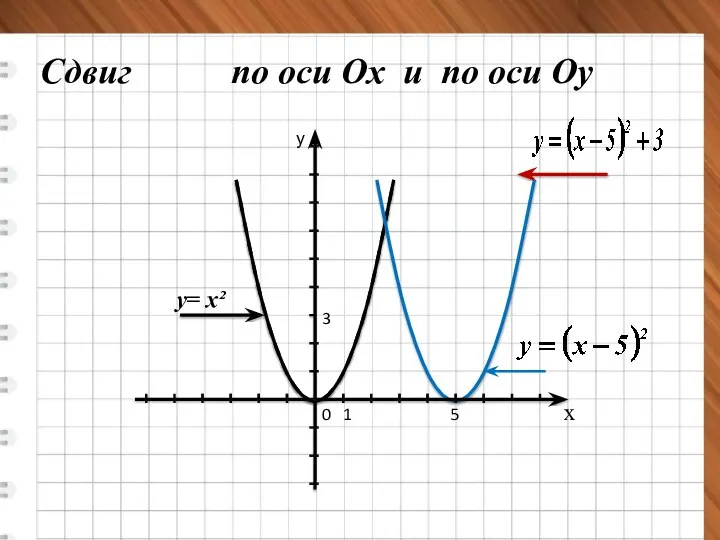
х
у
0 1
у= х²
Сдвиг по оси Ох и по оси Оу
3 5

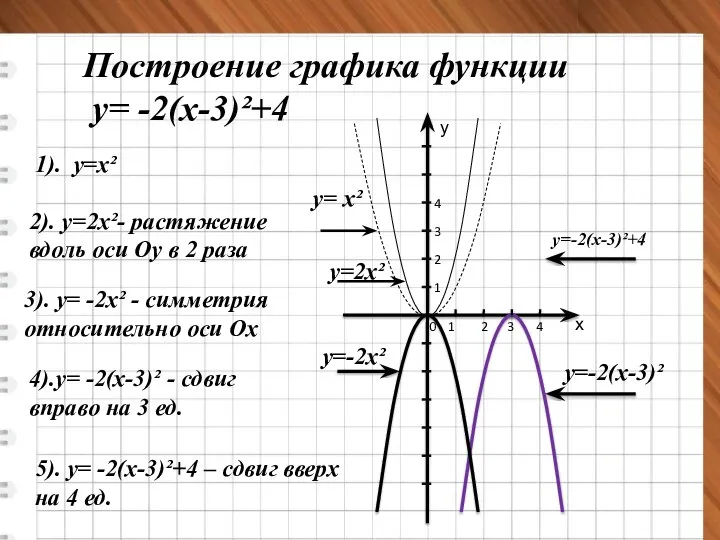
Построение графика функции
у= -2(х-3)²+4
0 1 2 3 4
1
2
3
4
у
х
у= х²
у=2х²
у=-2х²
у=-2(х-3)²
у=-2(х-3)²+4
1). у=х²
2). у=2х²- растяжение вдоль оси Оу в 2 раза
3). у= -2х² - симметрия относительно оси Ох
4).у= -2(х-3)² - сдвиг вправо на 3 ед.
5). у= -2(х-3)²+4 – сдвиг вверх на 4 ед.

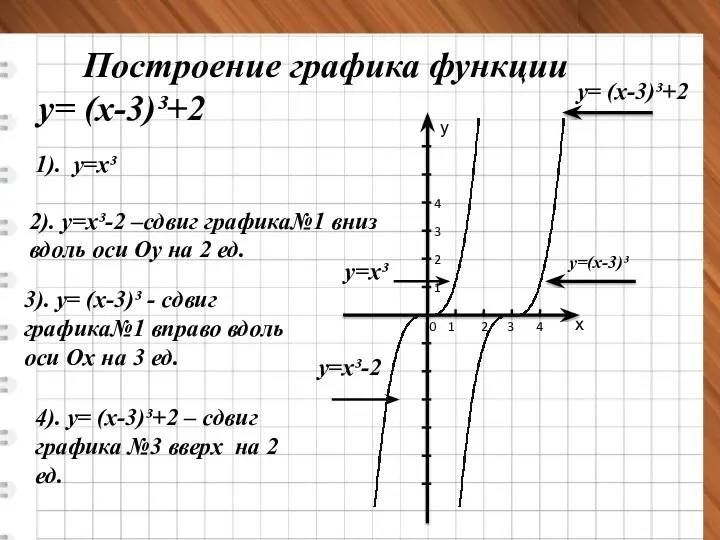
Построение графика функции
у= (х-3)³+2
0 1 2 3 4
1
2
3
4
у
х
у= (х-3)³+2 у=х³-2
у=х³
у=(х-3)³
1). у=х³
2). у=х³-2 –сдвиг графика№1 вниз вдоль оси Оу на 2 ед.
3). у= (х-3)³ - сдвиг графика№1 вправо вдоль оси Ох на 3 ед.
4). у= (х-3)³+2 – сдвиг графика №3 вверх на 2 ед.

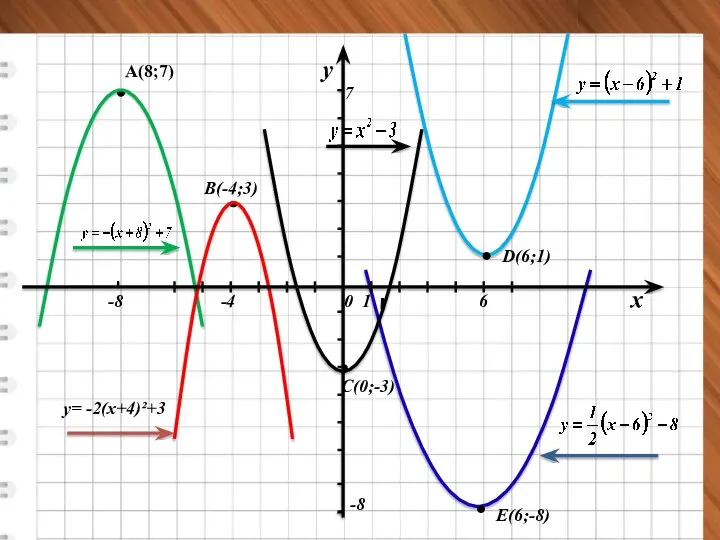
B(-4;3)
у= -2(х+4)²+3
A(8;7)
C(0;-3)
D(6;1)
E(6;-8)
6
-4
-8
-8
7
у
х
0 1

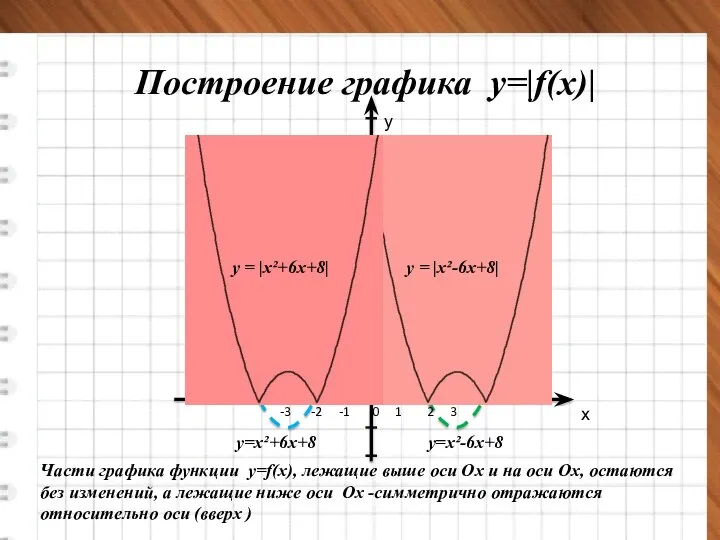
Построение графика y=|f(x)|
у=х²-6х+8
у=х²+6х+8
у = |х²-6х+8|
у = |х²+6х+8|
Части графика функции у=f(x), лежащие выше оси Ох и на оси Ох, остаются без изменений, а лежащие ниже оси Ох -симметрично отражаются относительно оси (вверх )
у
х
0 1
2 3
-1
-2
-3

х
у
2
4
5
6
7
8
1
0 1
-1
-2
-1
-2
-3
-4
-5
3
3
4
5
6
-3
2
у = х²-4х+2
у = х²-4|х|+2
Построение графика y=f(|x|)
Часть графика функции у =f(x), лежащая левее оси Оу, удаляется , а часть, лежащая правее оси Оу - остается без изменения и симметрично отражается относительно оси Оу(влево). Точка графика, лежащая на оси Оу, остается неизменной

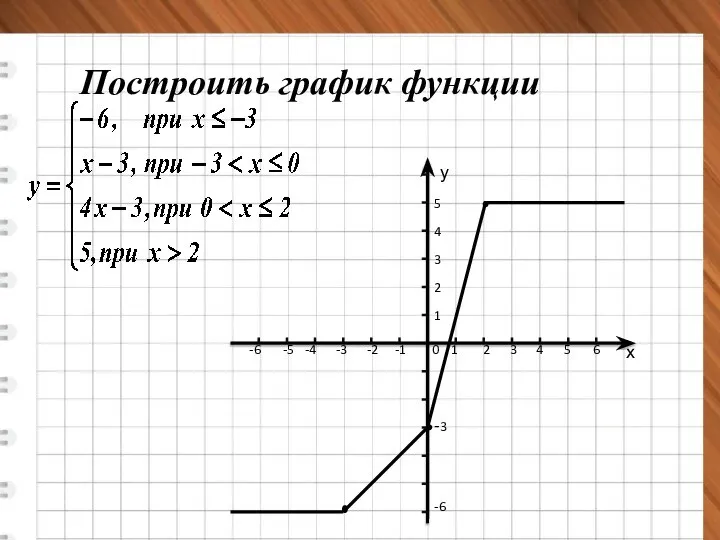
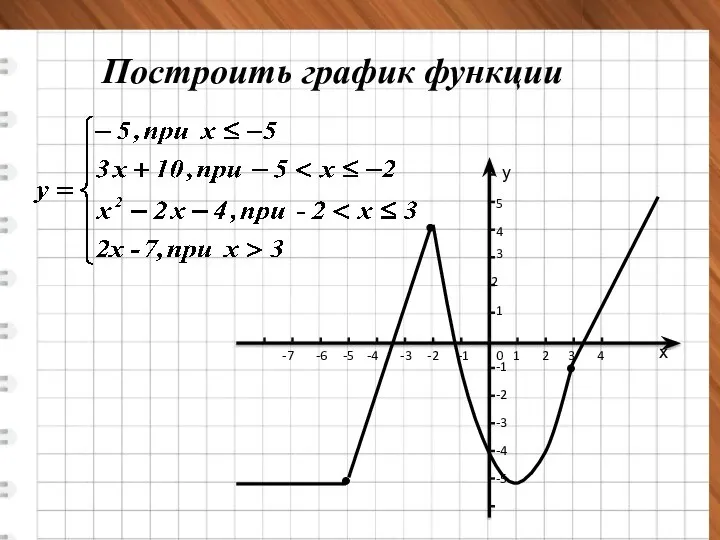
Построить график функции
0
1 2 3 4
5 6
5
4
3
2
1
-3
-6
-3
у
х
-1
-2
-4
-6 -5

1 2 3 4
0
-7 -6 -5
-4 -3 -2 -1
у
5
4
3
2
1
-1
-3
-2
-4
-5
х
Построить график функции