Содержание
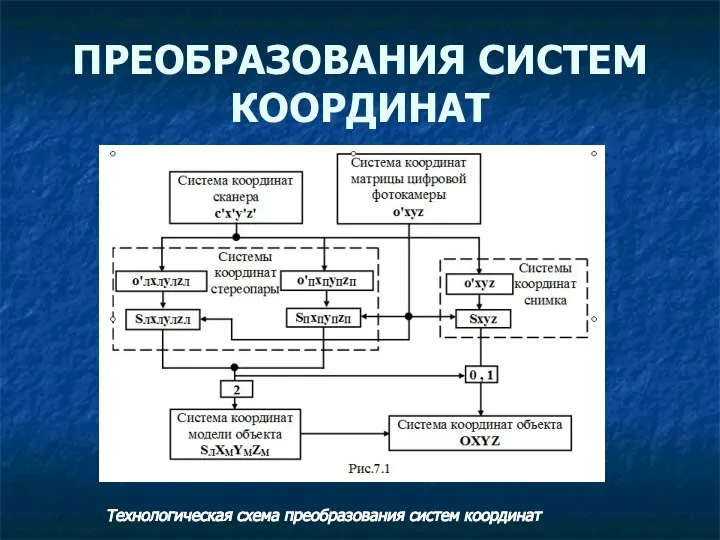
- 2. ПРЕОБРАЗОВАНИЯ СИСТЕМ КООРДИНАТ Технологическая схема преобразования систем координат
- 3. Фотограмметрическая обработка снимков состоит из последовательных преобразований координат. На рис приведена цепочка таких преобразований координат при
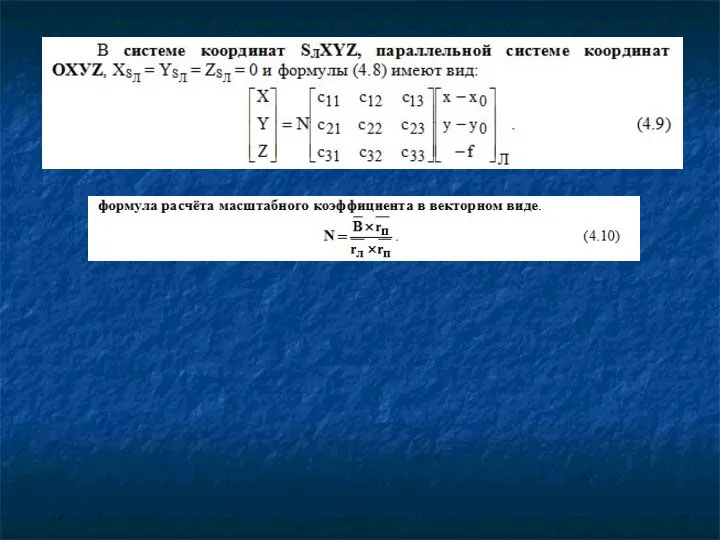
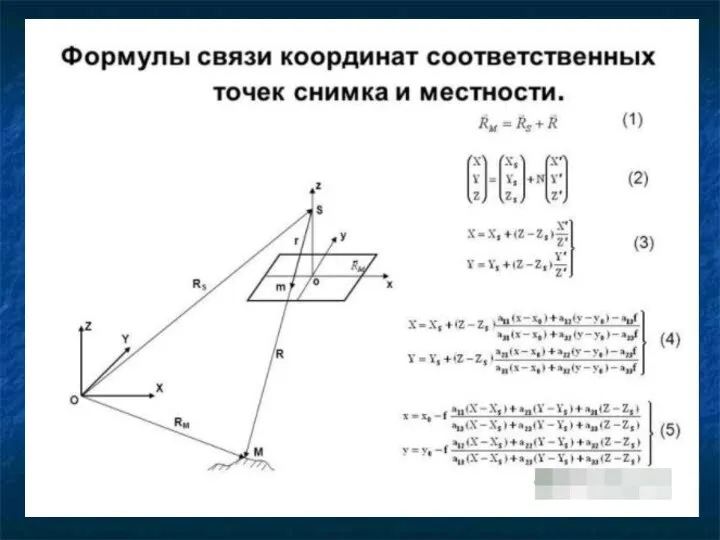
- 4. Координаты точек стереопары и снимка можно преобразовать сразу в систему координат OXYZ объекта, если известны с
- 5. Преобразование координат из системы координат сканера в систему координат снимка с началом в его центре проекции
- 7. На втором этапе вычисленные координаты x, y, z = 0 дополняют элементами внутреннего ориентирования x0, y0,
- 8. Преобразование координат из систем координат стереопары в систему координат объекта
- 10. !!
- 13. Угол поворота ω называется поперечным (тангаж для самолета) и определяет вращение вокруг оси ox, угол поворота
- 14. Формулы направляющих косинусов
- 16. Преобразование координат из систем координат стереопары идеального случая аэросъёмки в систему координат объекта
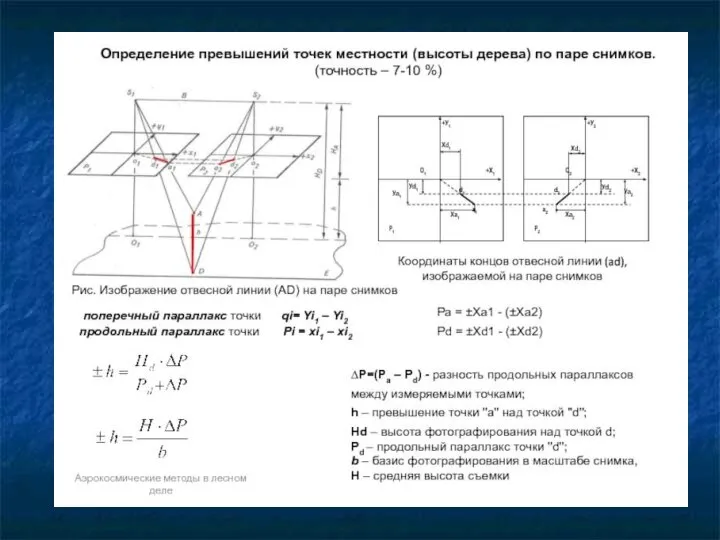
- 18. Т.к. высота фотографирования Н над точками, изобразившимися на снимке, меняется из-за рельефа местности, можно сделать вывод,
- 19. Причины появления продольного и поперечного параллаксов
- 20. Что касается поперечного параллакса q = yЛ - yП, то он возникает из-за различия в величинах
- 24. Скачать презентацию

















 Сокращение дробей. Самоанализ
Сокращение дробей. Самоанализ Геометрический конструктор GeoGebra
Геометрический конструктор GeoGebra Кусочная функция
Кусочная функция Презентация на тему Число 0 Цифра 0
Презентация на тему Число 0 Цифра 0  Повторение по математике
Повторение по математике 9fc9887af90115bf
9fc9887af90115bf Урок математики 20.09
Урок математики 20.09 Презентация на тему Повторяем таблицу умножения
Презентация на тему Повторяем таблицу умножения  Степенная функция
Степенная функция Нечеткие числа
Нечеткие числа Теорема Пифагора
Теорема Пифагора Дифференциальные уравнения и их применение в медицинской практике. Элементы комбинаторики. Случайные величины
Дифференциальные уравнения и их применение в медицинской практике. Элементы комбинаторики. Случайные величины Процент
Процент Презентация на тему НЕРАВЕНСТВО ТРЕУГОЛЬНИКА
Презентация на тему НЕРАВЕНСТВО ТРЕУГОЛЬНИКА  Теорема Виета. Устная работа
Теорема Виета. Устная работа Циркуль. Учимся работать циркулем (2 класс, технология)
Циркуль. Учимся работать циркулем (2 класс, технология) Решение текстовых задач. 5 класс
Решение текстовых задач. 5 класс Литр. Задачи
Литр. Задачи Презентация на тему КВН по информатике и математике
Презентация на тему КВН по информатике и математике  Описанная окружность треугольника
Описанная окружность треугольника Презентация на тему Аксиома параллельных прямых
Презентация на тему Аксиома параллельных прямых  Правильные многогранники в природе
Правильные многогранники в природе Деление одночлена на одночлен
Деление одночлена на одночлен Математический КВН. Счет и вычисления
Математический КВН. Счет и вычисления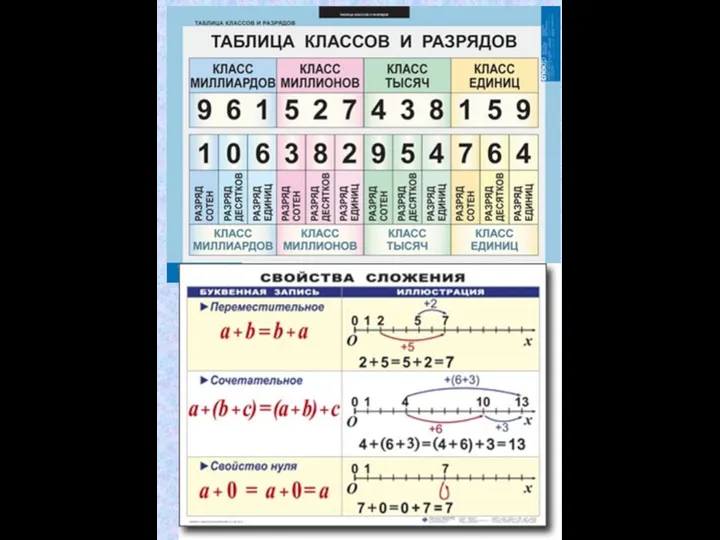 Таблица классов и разрядов. Свойства сложения
Таблица классов и разрядов. Свойства сложения Спасение похищенных чисел. Урок-сказка
Спасение похищенных чисел. Урок-сказка Формулы сокращенного умножения. Интерактивный плакат
Формулы сокращенного умножения. Интерактивный плакат Произведение многочленов
Произведение многочленов