Содержание
- 2. Наумова Ирина Михайловна Сегодня мы рассмотрим Построение графика функции y = cos x; Свойства функции y
- 3. Наумова Ирина Михайловна Построение графика Функция y = cos x определена на всей числовой прямой и
- 4. Наумова Ирина Михайловна Как использовать периодичность и четность при построении Так как функция периодическая с периодом
- 5. Наумова Ирина Михайловна Найдем несколько точек для построения графика на отрезке [0; π] и отразим, полученную
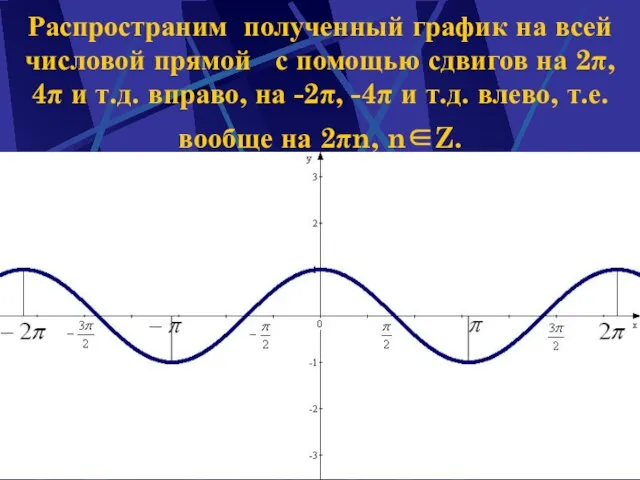
- 6. Наумова Ирина Михайловна Распространим полученный график на всей числовой прямой с помощью сдвигов на 2π, 4π
- 7. Наумова Ирина Михайловна Итак, график функции y = cos x построен геометрически на всей числовой прямой,
- 8. Наумова Ирина Михайловна Для этого нужно вспомнить Как найти область определения и множество значений тригонометрических функций;
- 9. Наумова Ирина Михайловна Область определения Каждому действительному числу х соответствует единственная точка единичной окружности, получаемая поворотом
- 10. Наумова Ирина Михайловна Множество значений Чтобы найти множество значений функции y = cos x, нужно выяснить,
- 11. Наумова Ирина Михайловна Периодичность Функция y = f (x) называется периодической, если существует такое число Т
- 12. Наумова Ирина Михайловна Четность, нечетность Функция y = f (x) называется четной, если для каждого значения
- 13. Наумова Ирина Михайловна Возрастание, убывание Функция y = f(x) называется возрастающей, если наибольшему (наименьшему) значению функции
- 14. Наумова Ирина Михайловна Нули функции, положительные и отрицательные значения, наименьшее и наибольшее значения. Для того чтобы
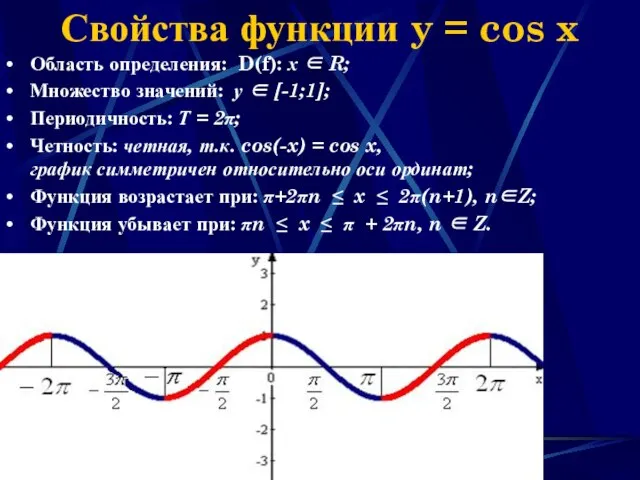
- 15. Наумова Ирина Михайловна Свойства функции y = cos x Область определения: D(f): х ∈ R; Множество
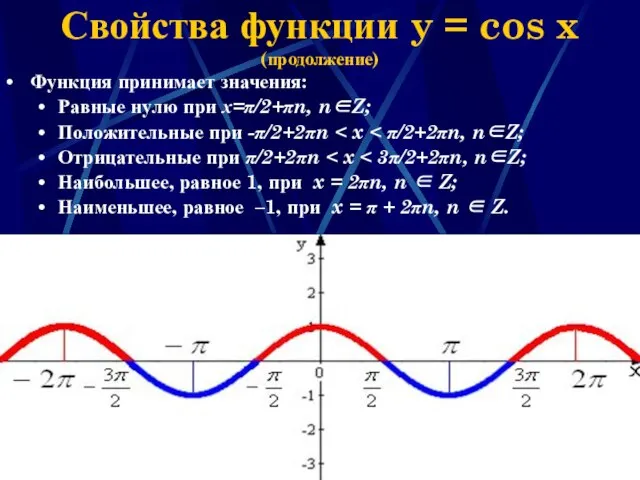
- 16. Наумова Ирина Михайловна Свойства функции y = cos x (продолжение) Функция принимает значения: Равные нулю при
- 17. Наумова Ирина Михайловна Преобразование графика функции y = cos x Изменение функции y = cos x
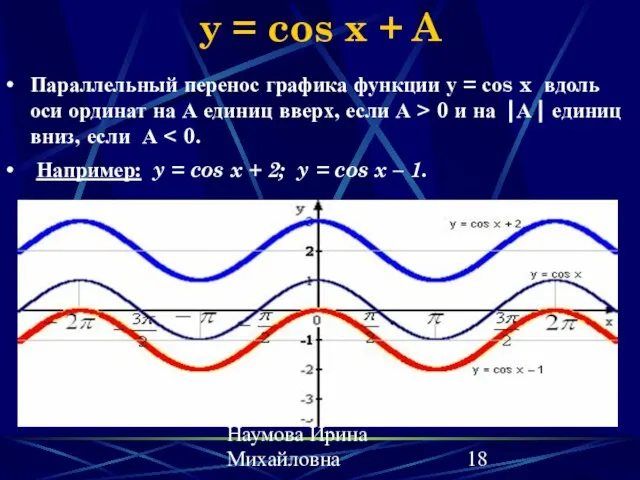
- 18. Наумова Ирина Михайловна y = cos x + A Параллельный перенос графика функции у = соs
- 19. Наумова Ирина Михайловна y = cos x + A (свойства) Изменяются множество значений функции; наибольшее (наименьшее)
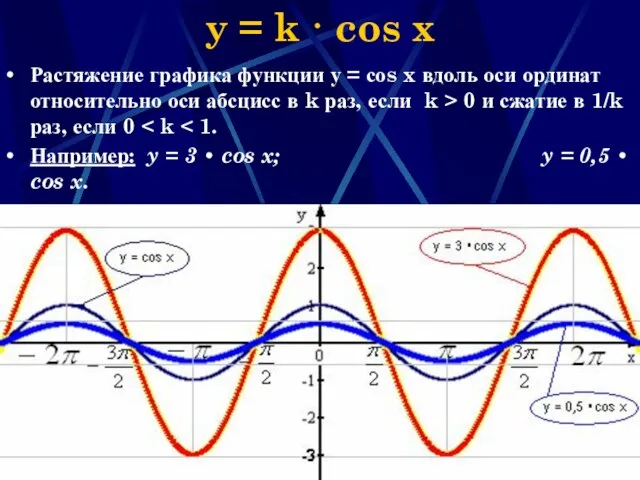
- 20. Наумова Ирина Михайловна y = k · cos x Растяжение графика функции у = соs x
- 21. Наумова Ирина Михайловна y = k · cos x (свойства) Изменяется множество значений функции; наибольшее (наименьшее)
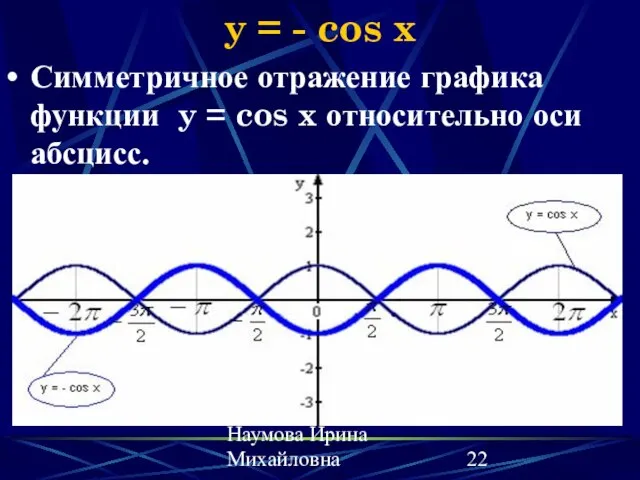
- 22. Наумова Ирина Михайловна y = - cos x Симметричное отражение графика функции y = cos x
- 23. Наумова Ирина Михайловна y = - cos x (свойства) Изменяются промежутки возрастания (убывания); промежутки положительных (отрицательных)
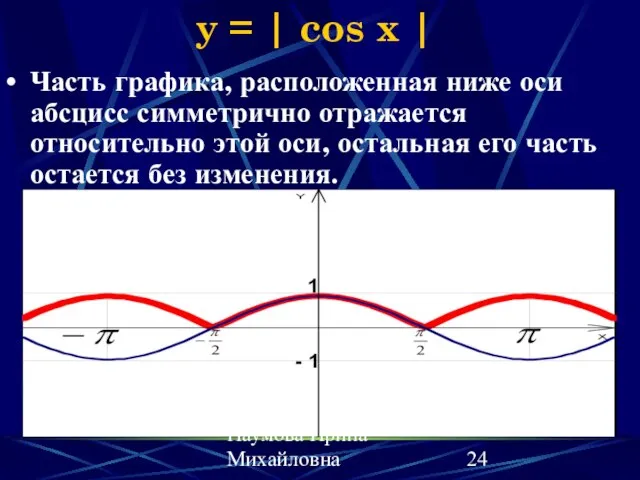
- 24. Наумова Ирина Михайловна y = | cos x | Часть графика, расположенная ниже оси абсцисс симметрично
- 25. Наумова Ирина Михайловна y = |cos x| (свойства) Изменяются: множество значений функции; период; промежутки возрастания (убывания);
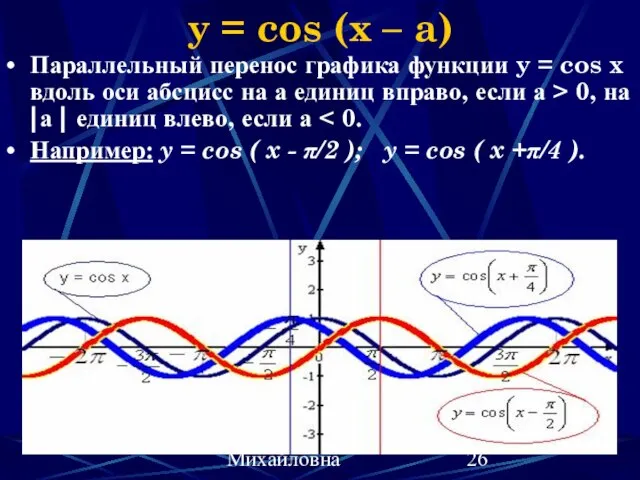
- 26. Наумова Ирина Михайловна y = cos (x – a) Параллельный перенос графика функции y = cos
- 27. Наумова Ирина Михайловна y = cos (x – a) (свойства) Изменяются: четность; промежутки возрастания (убывания); нули
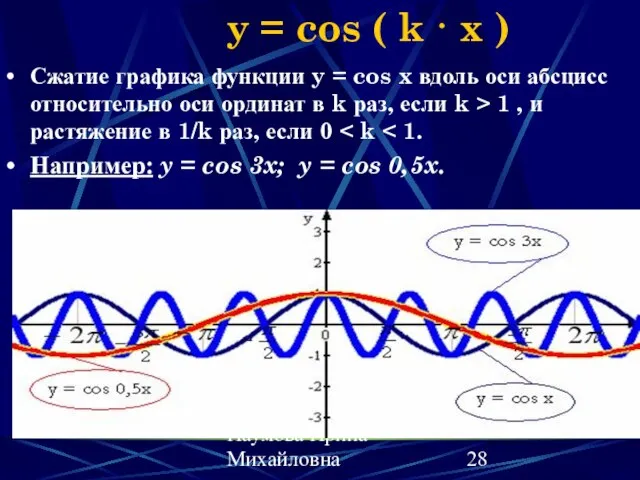
- 28. Наумова Ирина Михайловна y = cos ( k · x ) Сжатие графика функции y =
- 29. Наумова Ирина Михайловна y = cos ( k · x ) (свойства) Изменяются: период; промежутки возрастания
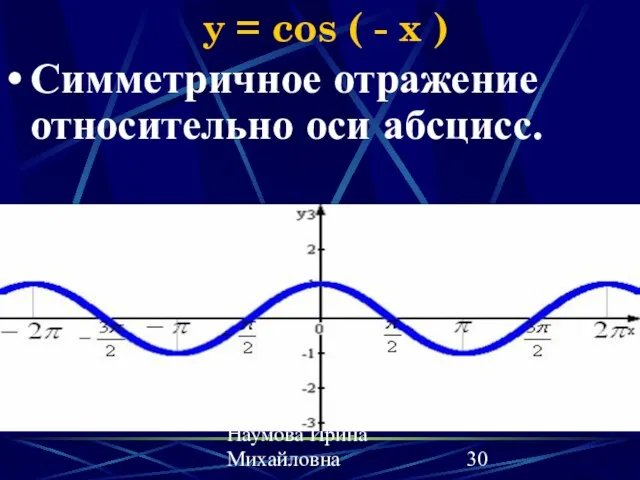
- 30. Наумова Ирина Михайловна y = cos ( - x ) Симметричное отражение относительно оси абсцисс.
- 31. Наумова Ирина Михайловна y = cos (-x) (свойства) В данном случае свойства функции не меняются, так
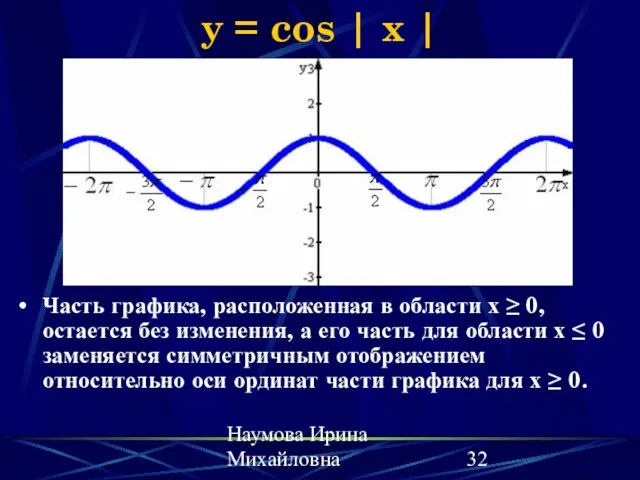
- 32. Наумова Ирина Михайловна y = cos | x | Часть графика, расположенная в области х ≥
- 33. Наумова Ирина Михайловна y = cos|x| (свойства) В данном случае свойства функции не меняются, так как
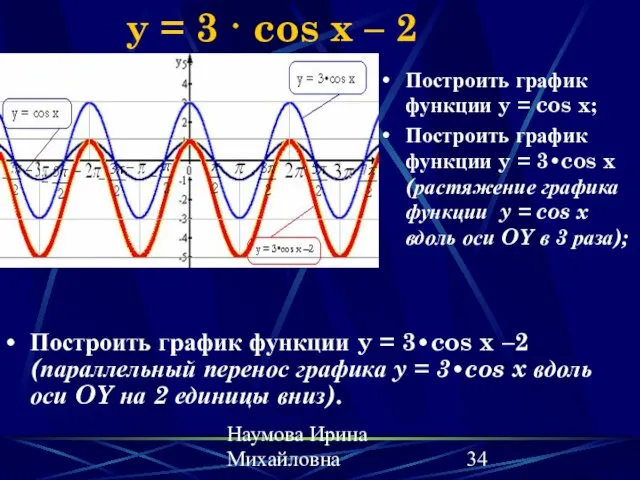
- 34. Наумова Ирина Михайловна y = 3 · cos x – 2 Построить график функции y =
- 35. Наумова Ирина Михайловна Свойства функции y = 3 · cos x – 2 Область определения: D(f):
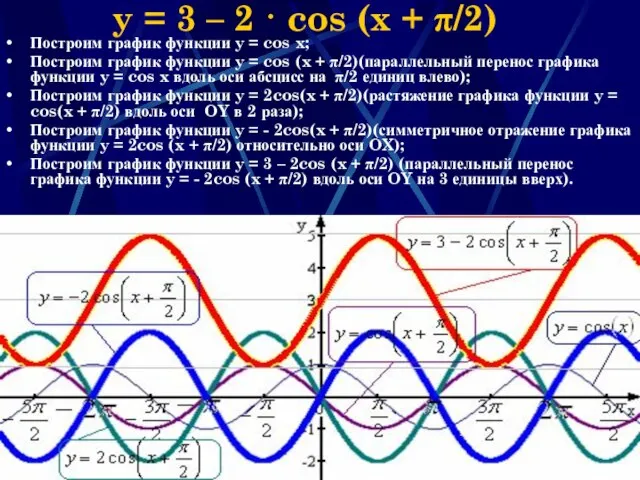
- 36. Наумова Ирина Михайловна y = 3 – 2 · cos (x + π/2) Построим график функции
- 38. Скачать презентацию






















 Презентация на тему ПРИМЕНЕНИЕ РАЗЛИЧНЫХ СПОСОБОВ РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ МНОГОЧЛЕНА
Презентация на тему ПРИМЕНЕНИЕ РАЗЛИЧНЫХ СПОСОБОВ РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ МНОГОЧЛЕНА  Симплексный метод планирования. Лекция 6
Симплексный метод планирования. Лекция 6 Геометрическое моделирование объекта шифрования на основе точечного исчисления Балюбы-Найдыша
Геометрическое моделирование объекта шифрования на основе точечного исчисления Балюбы-Найдыша Первообразная. Тренажер
Первообразная. Тренажер Основные характеристики средств измерений. Лекция 4
Основные характеристики средств измерений. Лекция 4 Корень n-ой степени и его свойства
Корень n-ой степени и его свойства Сумма
Сумма Презентация на тему Начертательная геометрия
Презентация на тему Начертательная геометрия  Математика на каждый день
Математика на каждый день Итоговой тест по геометрии. 9 класс
Итоговой тест по геометрии. 9 класс Час. Минута
Час. Минута Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7
Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7 Презентация на тему Распределительный закон умножения
Презентация на тему Распределительный закон умножения  Задача о нахождении стороны квадрата
Задача о нахождении стороны квадрата Учимся писать цифры
Учимся писать цифры Основы тригонометрии
Основы тригонометрии Набор инсулина в шприц
Набор инсулина в шприц Логарифм. Свойства логарифмов
Логарифм. Свойства логарифмов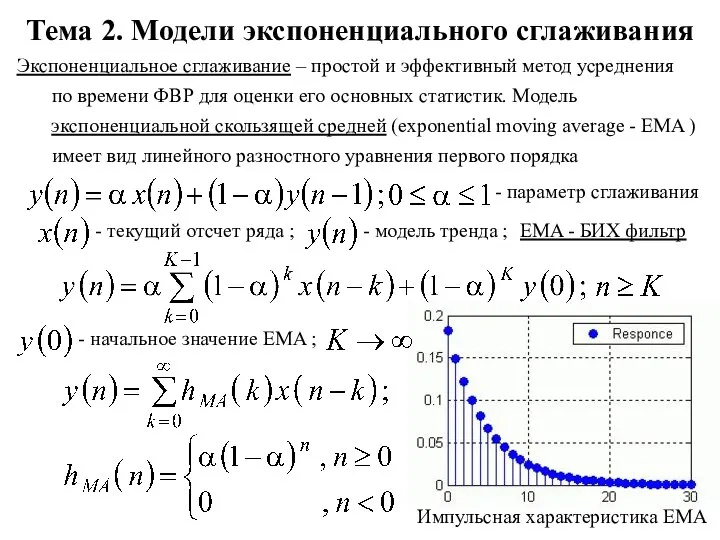 Модели экспоненциального сглаживания. Тема 2
Модели экспоненциального сглаживания. Тема 2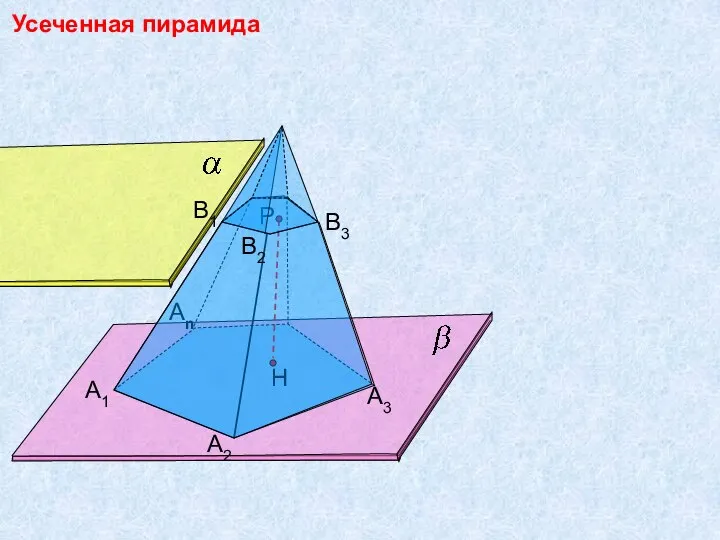 Усеченная пирамида
Усеченная пирамида Многоугольники в жизни
Многоугольники в жизни Ортогональное проектирование. Перпендикуляр и наклонная. Угол между прямой и плоскостью. (Практическая работа)
Ортогональное проектирование. Перпендикуляр и наклонная. Угол между прямой и плоскостью. (Практическая работа) Объёмные и плоские геометрические фигуры
Объёмные и плоские геометрические фигуры Пропорциональность величин. Урок 132
Пропорциональность величин. Урок 132 Логические основы обработки информации. Алгебра логики
Логические основы обработки информации. Алгебра логики Логарифмическая линейка
Логарифмическая линейка Задание В11, открытого банка ЕГЭ по математике (часть 2)
Задание В11, открытого банка ЕГЭ по математике (часть 2) Презентация на тему История возникновения геометрии
Презентация на тему История возникновения геометрии