Содержание
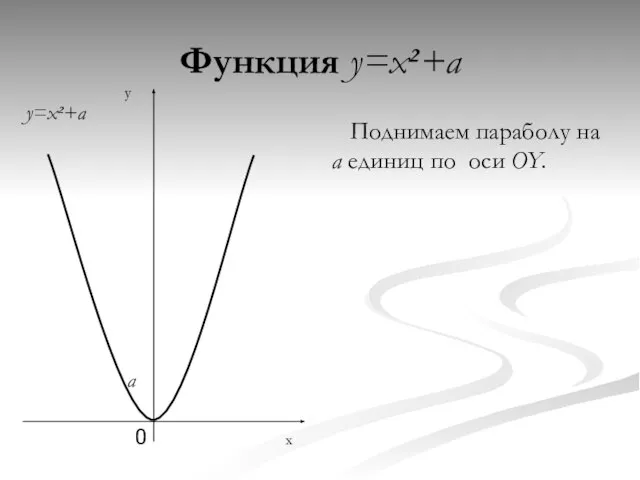
- 2. Функция y=x²+a Поднимаем параболу на a единиц по оси OY. x y 0 a y=x²+a
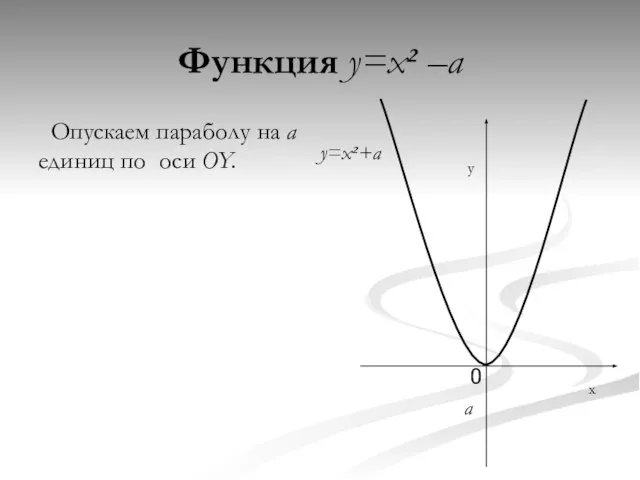
- 3. Функция y=x² –a Опускаем параболу на a единиц по оси OY. x y 0 a y=x²+a
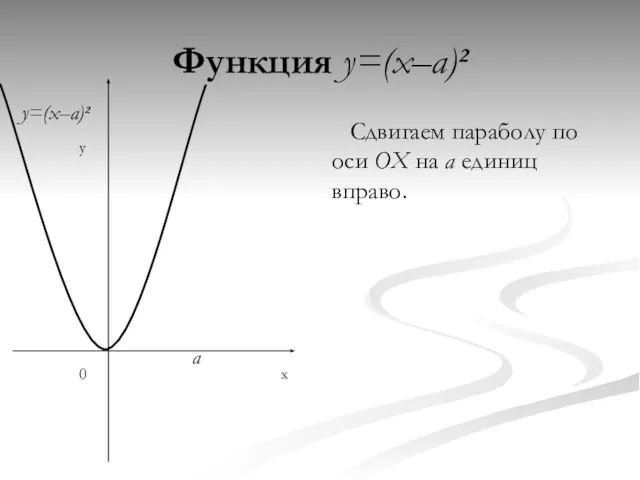
- 4. Функция y=(x–a)² Сдвигаем параболу по оси OX на a единиц вправо. y x 0 a y=(x–a)²
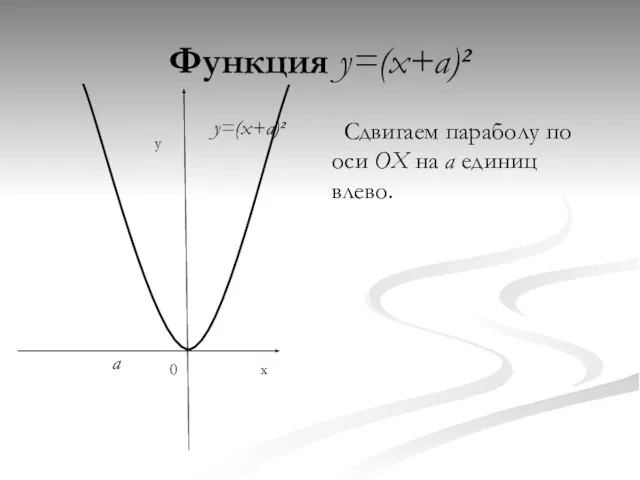
- 5. Функция y=(x+a)² Сдвигаем параболу по оси OX на a единиц влево. y x 0 a y=(x+a)²
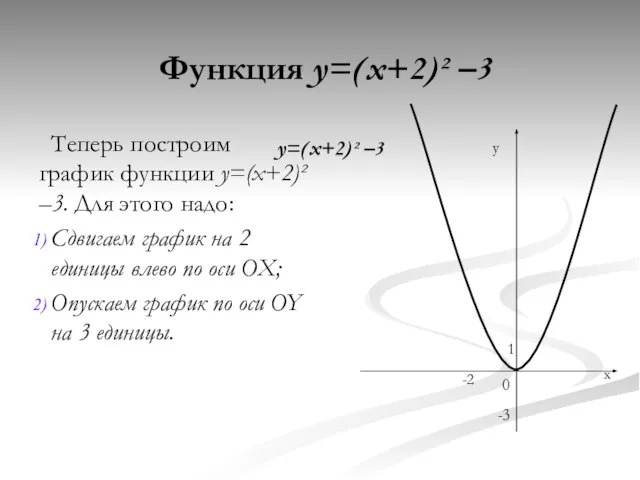
- 6. Функция y=(x+2)² –3 Теперь построим график функции y=(x+2)² –3. Для этого надо: Сдвигаем график на 2
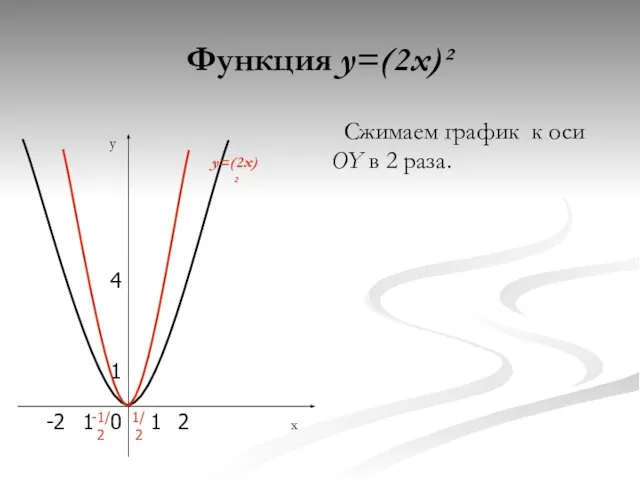
- 7. Функция y=(2x)² Сжимаем график к оси OY в 2 раза. y x 0 4 1 1
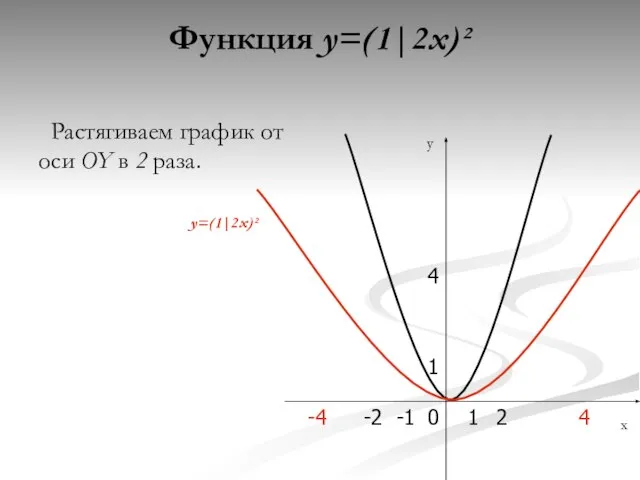
- 8. Функция y=(1|2x)² Растягиваем график от оси OY в 2 раза. 0 4 1 -1 1 2
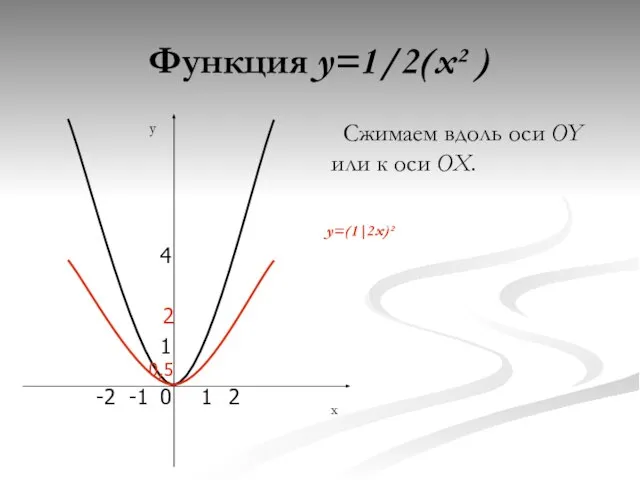
- 9. Функция y=1/2(x² ) Сжимаем вдоль оси OY или к оси OX. 0 4 1 -1 1
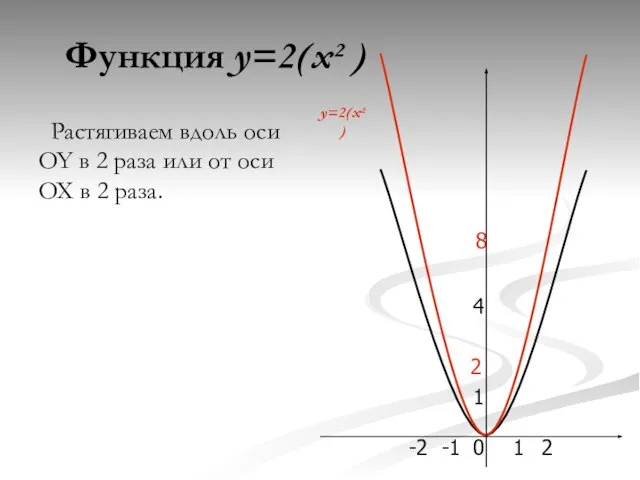
- 10. Функция y=2(x² ) 0 4 1 -1 1 2 -2 Растягиваем вдоль оси OY в 2
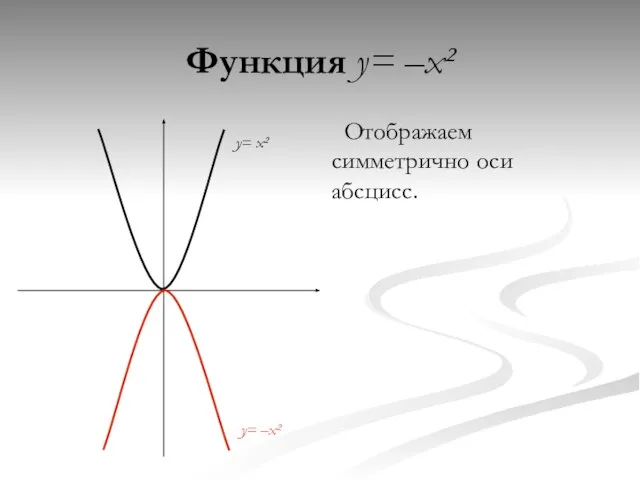
- 11. Функция y= –x² Отображаем симметрично оси абсцисс. y= –x² y= x²
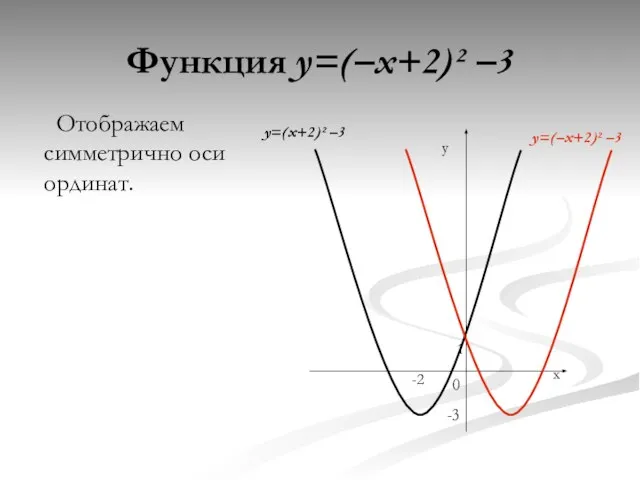
- 12. Функция y=(–x+2)² –3 Отображаем симметрично оси ординат. y 0 x -3 -2 1 y=(–x+2)² –3 y=(x+2)²
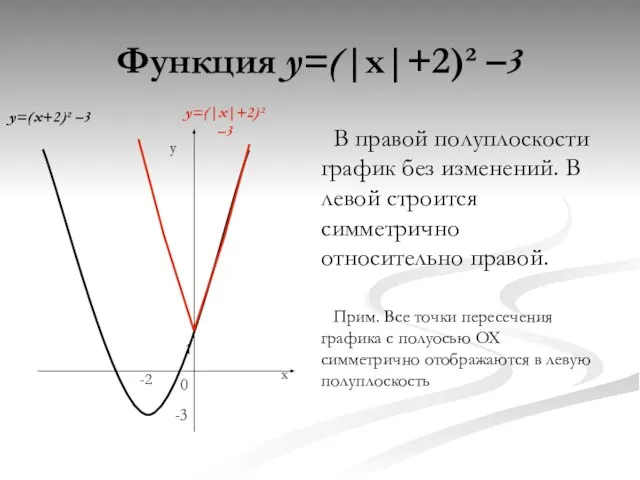
- 13. Функция y=(|x|+2)² –3 В правой полуплоскости график без изменений. В левой строится симметрично относительно правой. Прим.
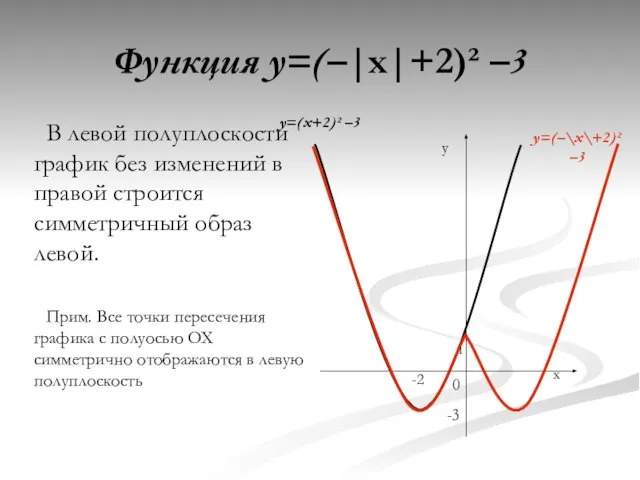
- 14. Функция y=(–|x|+2)² –3 В левой полуплоскости график без изменений в правой строится симметричный образ левой. Прим.
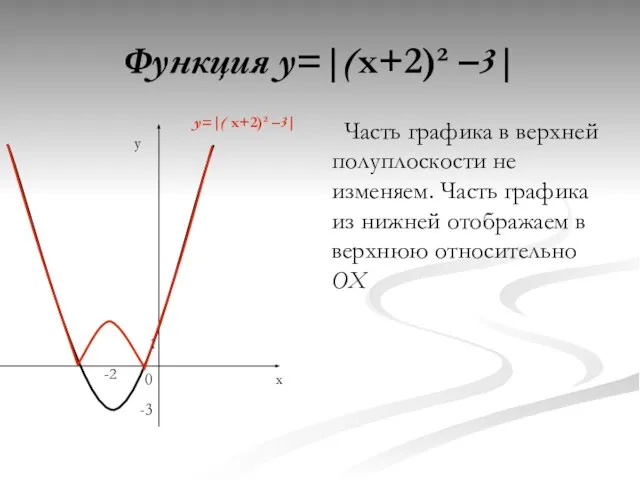
- 15. Функция y=|(x+2)² –3| Часть графика в верхней полуплоскости не изменяем. Часть графика из нижней отображаем в
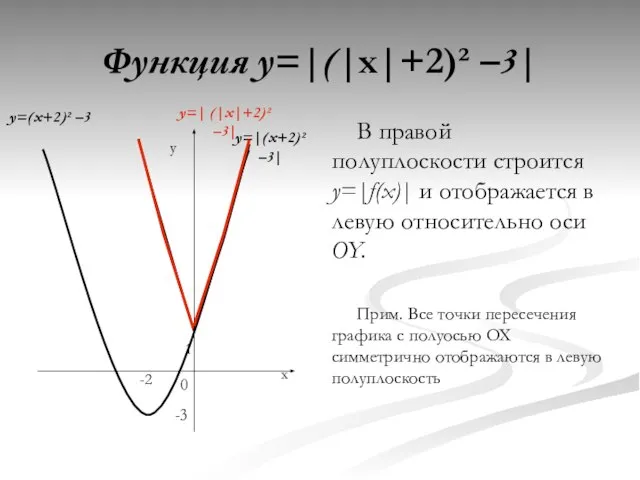
- 16. Функция y=|(|x|+2)² –3| В правой полуплоскости строится y=|f(x)| и отображается в левую относительно оси OY. Прим.
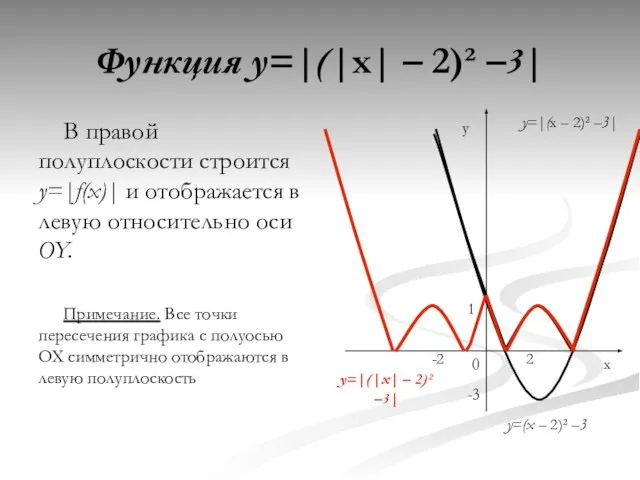
- 17. Функция y=|(|x| – 2)² –3| В правой полуплоскости строится y=|f(x)| и отображается в левую относительно оси
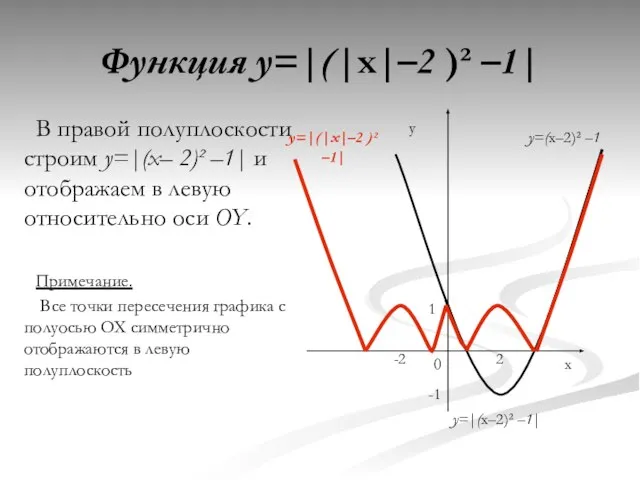
- 18. В правой полуплоскости строим y=|(x– 2)² –1| и отображаем в левую относительно оси OY. Примечание. Все
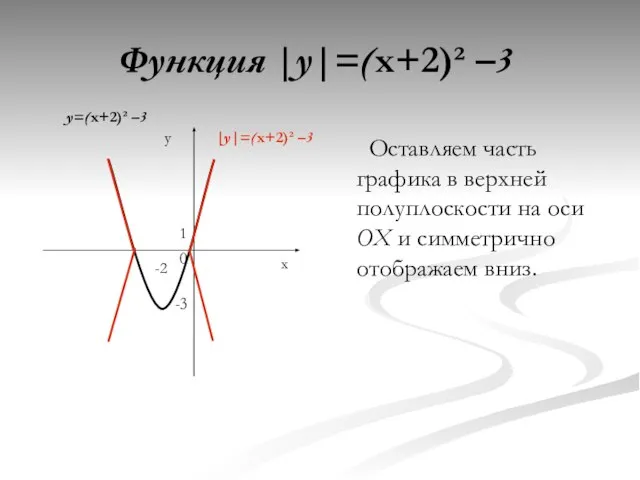
- 19. Функция |y|=(x+2)² –3 y 0 x -3 -2 1 Оставляем часть графика в верхней полуплоскости на
- 21. Скачать презентацию
 Свойства логарифмов
Свойства логарифмов Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Координатная плоскость
Координатная плоскость Показательные и логарифмические уравнения, системы, неравенства
Показательные и логарифмические уравнения, системы, неравенства Числа 6 и 7. Письмо цифры 7 (1 класс)
Числа 6 и 7. Письмо цифры 7 (1 класс) Справочник по геометрии
Справочник по геометрии Презентация на тему Высказывания со словами: есть, существует, некоторые
Презентация на тему Высказывания со словами: есть, существует, некоторые  Подстановки, оптимизация и решение дифференциальных уравнений (задача Коши)
Подстановки, оптимизация и решение дифференциальных уравнений (задача Коши) Решение задач по теме: Объем цилиндра 11 класс
Решение задач по теме: Объем цилиндра 11 класс Распределительное свойства умножения
Распределительное свойства умножения Общее решение неполного квадратного уравнения. 8 класс
Общее решение неполного квадратного уравнения. 8 класс Задания по геометрии
Задания по геометрии Составление алгоритма
Составление алгоритма Конус
Конус Логарифмические уравнения
Логарифмические уравнения Плоскости
Плоскости Комплексные числа и действия над ними
Комплексные числа и действия над ними Найди значение выражений
Найди значение выражений Размерность. Единицы измерения
Размерность. Единицы измерения Определение вектора
Определение вектора Закрепление изученного. Решение задач
Закрепление изученного. Решение задач Понятие цилиндра
Понятие цилиндра Коэффициент корреляции
Коэффициент корреляции Презентация на тему Деление многозначного числа на однозначное
Презентация на тему Деление многозначного числа на однозначное  Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3
Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3 Умножение на 2. Проведите динозаврика по лабиринту (2)
Умножение на 2. Проведите динозаврика по лабиринту (2) Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Системы степенных неравенств
Системы степенных неравенств