Слайд 2
Цели:
ввести понятие квадратичной функции;
научится строить график функции у=ах2 + ах

+с и описывать свойства данной функции по графику;
установить закономерность между графиком функции у=ах2 и значением коэффициента а.
Слайд 3Два жучка бежали в домик.
Им навстречу муравей.
Сколько будет насекомых?
Сосчитай - ка их

скорей!
Слайд 4Определение.
Квадратичной функцией называется функция, которую можно задать формулой вида у=ах2+bx+c, где

х – независимая переменная, а, b и с – некоторые числа, причем а≠0.
Слайд 5Из приведенных примеров укажите те функции,
которые являются квадратичными. Для квадратичных
функций

назовите коэффициенты.
Слайд 9Диктант.
Функция у=ах2, ее график и свойства.

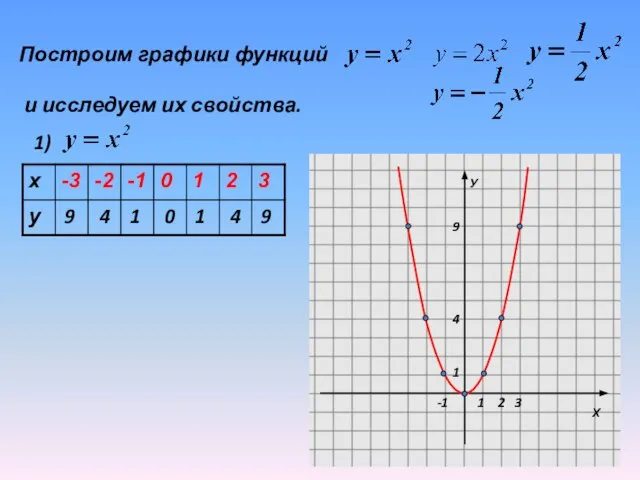
Слайд 10Построим графики функций
и исследуем их свойства.
1)
9
4
1
0
1
4
9
Слайд 11Построим графики функций
и исследуем их свойства.
1)
9
4
1
0
1
4
9
1. D(y): R
2. у=0, если
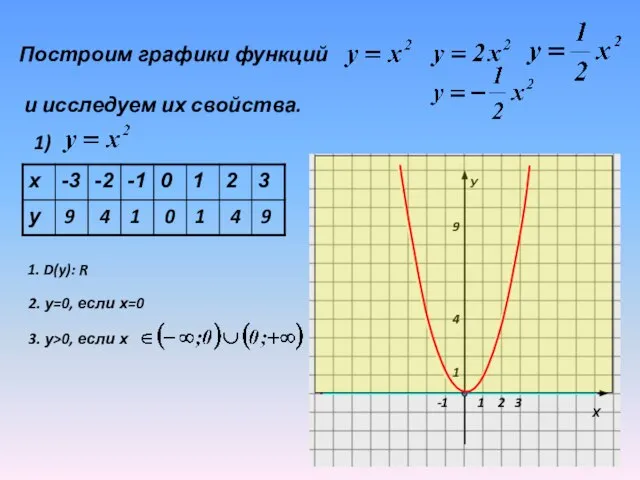
Слайд 12Построим графики функций
и исследуем их свойства.
1)
9
4
1
0
1
4
9
1. D(y): R
2. у=0, если
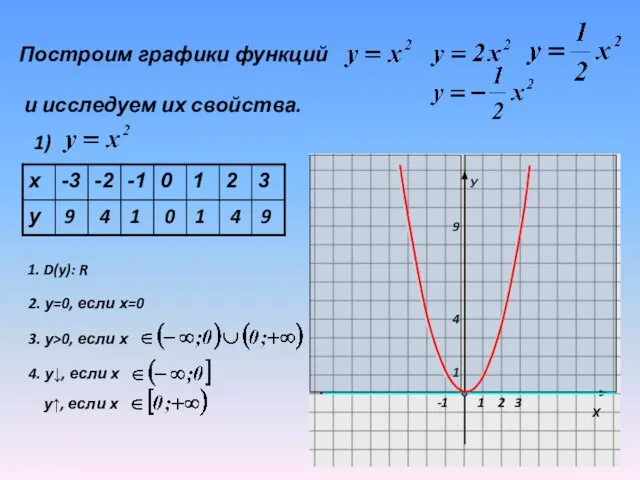
х=0
3. у>0, если х
4. у↓, если х
у↑, если х
Слайд 13Построим графики функций
и исследуем их свойства.
1)
9
4
1
0
1
4
9
1. D(y): R
2. у=0, если
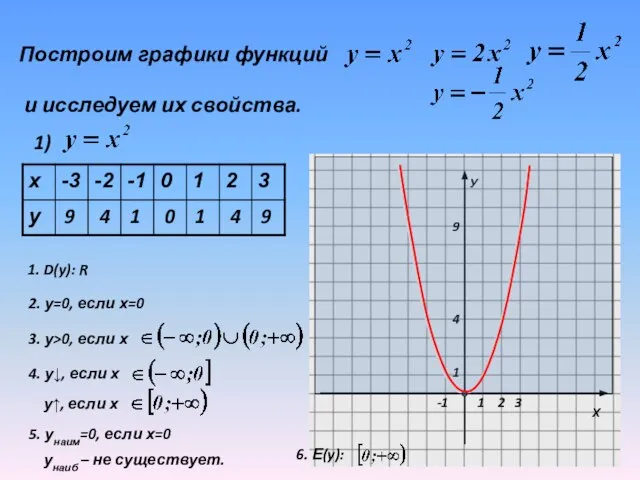
х=0
3. у>0, если х
4. у↓, если х
у↑, если х
5. унаим=0, если х=0
унаиб – не существует.
6. Е(y):
Слайд 14Построим графики функций
и исследуем их свойства.
2)
18
8
2
0
2
8
18
Есть ли различия в
свойствах
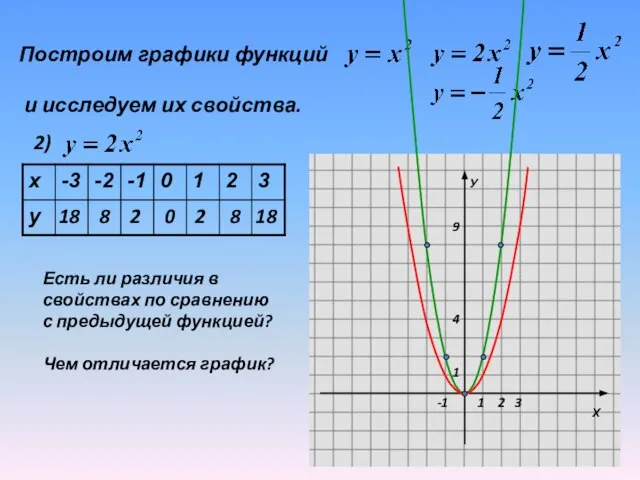
по сравнению
с предыдущей функцией?
Чем отличается график?
Слайд 15 График функции у=kx2 может быть получен из графика функции у=x2 путем

растяжения его вдоль оси Оу в k раз (k-натуральное число).
Слайд 16Построим графики функций
и исследуем их свойства.
3)
4,5
2
0,5
0
0,5
2
4,5
Есть ли различия в
свойствах
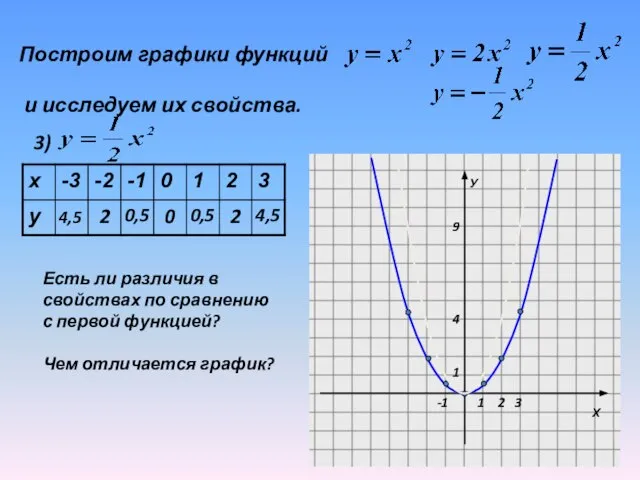
по сравнению
с первой функцией?
Чем отличается график?
Слайд 17График функции у= x2 может
быть получен из графика функции у=x2 путем

сжатия его вдоль оси Оу в k раз (k-натуральное число).
Слайд 18Построим графики функций
и исследуем их свойства.
4)
-4,5
-2
-0,5
0
-0,5
-2
-4,5
Есть ли различия в
свойствах
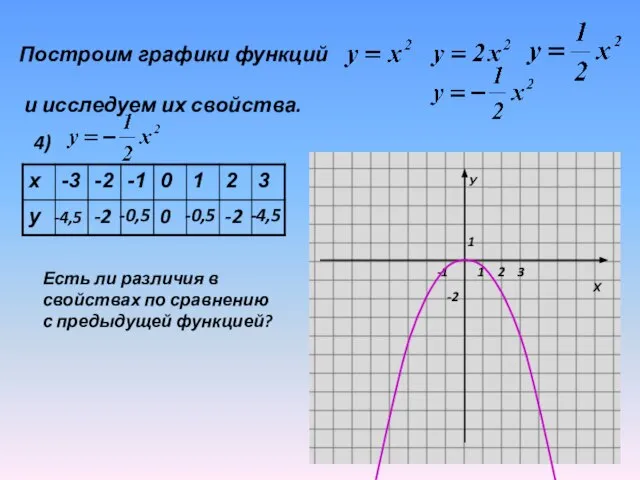
по сравнению
с предыдущей функцией?
Слайд 19Построим графики функций
и исследуем их свойства.
4)
-4,5
-2
-0,5
0
-0,5
-2
-4,5
1. D(y): R
2. у=0, если
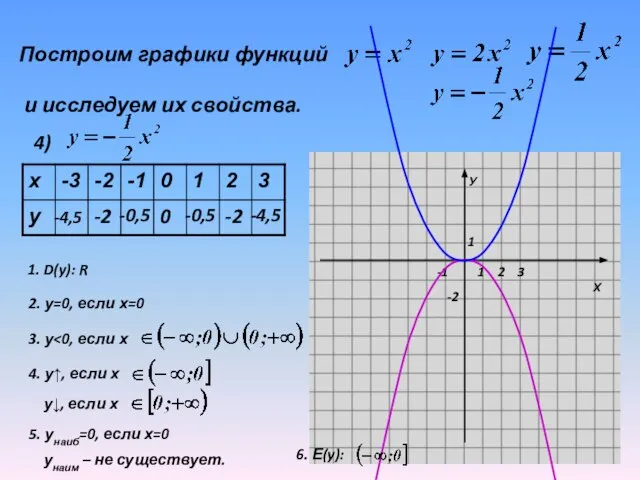
х=0
3. у<0, если х
4. у↑, если х
у↓, если х
5. унаиб=0, если х=0
унаим – не существует.
6. Е(y):
Слайд 20 График функции у=ах2 симметричен графику функции у=-ах2 относительно оси Ох.
Если а>0,

то ветви параболы направлены…
Если а<0, то ветви параболы
направлены…


















 Математические модели электромеханических объектов управления
Математические модели электромеханических объектов управления Алгебра логики. Понятие алгебры логики
Алгебра логики. Понятие алгебры логики Число и цифра 2
Число и цифра 2 mypresentation.ru
mypresentation.ru kombinatorika_lektsia
kombinatorika_lektsia Прямая пропорциональность и ее график
Прямая пропорциональность и ее график Задачи на расстояния в пространстве
Задачи на расстояния в пространстве Сложение смешанных дробей
Сложение смешанных дробей Окружность, круг и их элементы. Центральный угол
Окружность, круг и их элементы. Центральный угол Нумерация. Сложение и вычитание. Геометрические фигуры и величины
Нумерация. Сложение и вычитание. Геометрические фигуры и величины Задачи на готовых чертежах. Подобные треугольники
Задачи на готовых чертежах. Подобные треугольники Счастливый случай. Урок- зачет по подготовке к ГИА
Счастливый случай. Урок- зачет по подготовке к ГИА Десятичные и натуральные логарифмы
Десятичные и натуральные логарифмы Презентация на тему Одночлены. Многочлены
Презентация на тему Одночлены. Многочлены  Решение квадратных уравнений выделением квадрата двучлена
Решение квадратных уравнений выделением квадрата двучлена Алгебраические дроби. 7 класс
Алгебраические дроби. 7 класс Презентация на тему Число и цифра 9
Презентация на тему Число и цифра 9  Задачи на проценты. Проценты в различных сферах деятельности человека
Задачи на проценты. Проценты в различных сферах деятельности человека Замечательные точки и линии треугольника. 9 класс
Замечательные точки и линии треугольника. 9 класс Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Имитационное моделирование
Имитационное моделирование Движение
Движение Презентация на тему Решение задач на готовых чертежах. Окружность. Центральные и вписанные углы
Презентация на тему Решение задач на готовых чертежах. Окружность. Центральные и вписанные углы  Свойства логарифмов
Свойства логарифмов Презентация на тему Положительные и отрицательные числа
Презентация на тему Положительные и отрицательные числа  Способы быстрого счета
Способы быстрого счета Итоговое повторение. Алгебра. 8 класс
Итоговое повторение. Алгебра. 8 класс Математика + естествознание
Математика + естествознание