Слайд 2Графики функций
у=ах2+n и у=а(х-m)2
Тема урока:
Всякое учение и всякое обучение основано на

некотором уже ранее имеющемся знании
Аристотель
Слайд 3Устный опрос
Сформулировать определение квадратичной функции;
Что является графиком квадратичной функции?
Сформулировать свойства квадратичной

функции у=ах2 при а>0, a<0.
Как из графика функции у=ах2 можно получить график функции у=ах2 + n; график функции у=а(х-m)2
Слайд 4Задание 1
Задание 2
ЗАДАНИЕ 3
Слайд 5Практическое выполнение задания в тетради
В одной системе координат построить графики функций в

тетрадях:
А)у = 1/2 x2; y = 1/2x2 +4; y =1/2x2 -3;
Б)у=-1/3х2 , y = -1/3(x-2)2 , y = -1/3(x+3)2 ,
Слайд 6Задание 1
Построить в одной системе
координат графики функции
y=x2 , y=x2-5 и

y=x2+5
Слайд 7Задание 2
Построить в одной системе
координат графики функций у=2х2, у=2(х-5)2, у=2(х+4)2

Слайд 8Задание 3
Построить в одной системе координат графики функций у=2х2 ,у= 2(х-5)2+3,
у=-2(х+4)2-5

Слайд 9Проверь себя
Задание 1
Задание 2
Задание 3

Слайд 10Вывод:
График функции у=ах2 +n является
параболой, которую можно получить из
графика
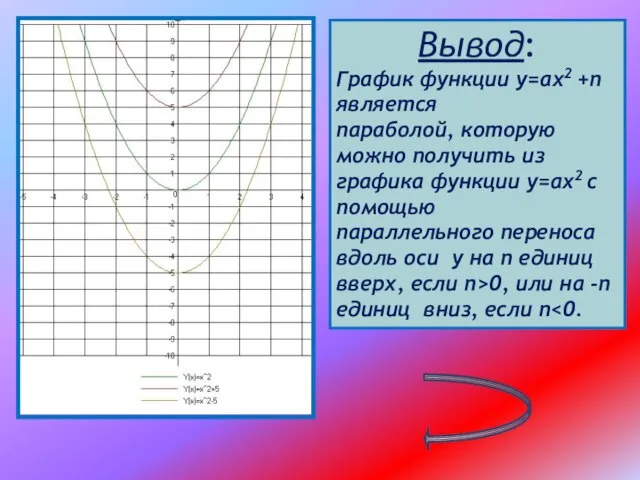
функции у=ах2 с помощью
параллельного переноса вдоль оси у на n единиц вверх, если n>0, или на -n единиц вниз, если n<0.
Слайд 11 Вывод :
График функции у=а(х-m)2 является параболой, которую можно получить из графика
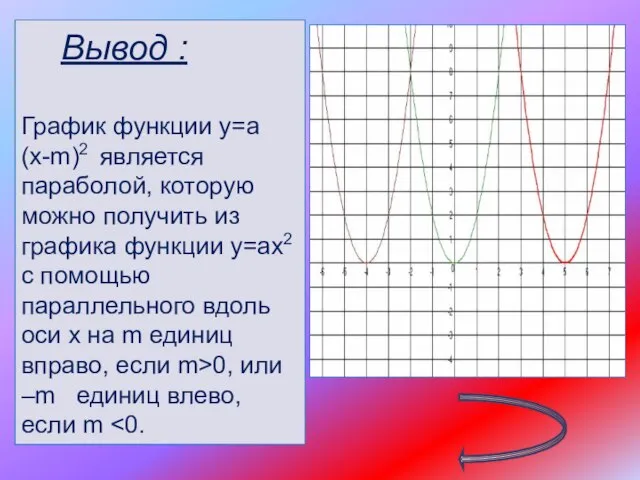
функции у=ах2 с помощью параллельного вдоль оси х на m единиц вправо, если m>0, или –m единиц влево, если m <0.
Слайд 12Вывод:
График функции у=а(х-m)2 +n является парабола, которую можно получить из графика
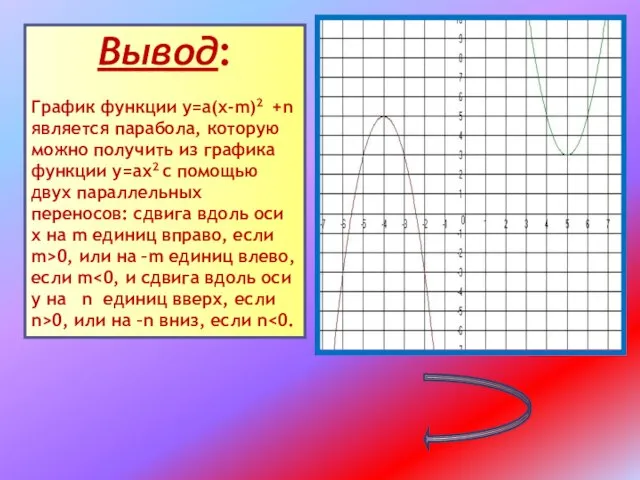
функции у=ах2 с помощью двух параллельных переносов: сдвига вдоль оси х на m единиц вправо, если m>0, или на –m единиц влево, если m<0, и сдвига вдоль оси у на n единиц вверх, если n>0, или на –n вниз, если n<0.











 Думаємо колективно, працюємо оперативно, сперечаємось доказово – це для всіх обов'язково
Думаємо колективно, працюємо оперативно, сперечаємось доказово – це для всіх обов'язково Доли. Устный счет
Доли. Устный счет Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Упрощение выражений. Урок-сказка
Упрощение выражений. Урок-сказка Решение уравнений
Решение уравнений Признаки классификации статистической сводки
Признаки классификации статистической сводки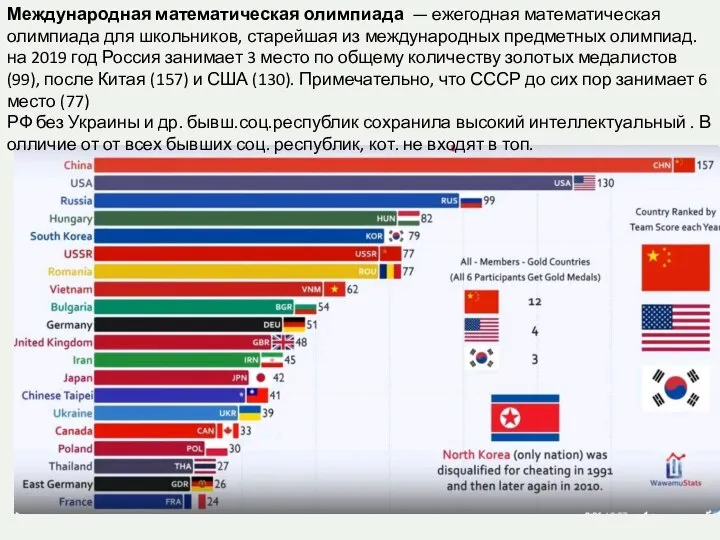 Международная математическая олимпиада
Международная математическая олимпиада Технология квантового обучения в преподавании математики
Технология квантового обучения в преподавании математики Сравнение отрезков и углов геометрических фигур
Сравнение отрезков и углов геометрических фигур Презентация на тему Математический КВН 8 класс
Презентация на тему Математический КВН 8 класс  Условия неопределенности выбора. Ограниченная рациональность
Условия неопределенности выбора. Ограниченная рациональность Векторы. Действия с векторами
Векторы. Действия с векторами Вычитание и сложение чисел
Вычитание и сложение чисел Нумерационные случаи сложения и вычитания чисел второго десятка
Нумерационные случаи сложения и вычитания чисел второго десятка Взаимное расположение графиков линейных функций. 7 класс
Взаимное расположение графиков линейных функций. 7 класс Обработка многократных измерений
Обработка многократных измерений Запомни координаты. Игра
Запомни координаты. Игра Теорема Пифагора для пятиклассников
Теорема Пифагора для пятиклассников Приложения производной
Приложения производной Порядок элемента. Теорема Лагранжа
Порядок элемента. Теорема Лагранжа Теорія множин. Відношення
Теорія множин. Відношення Параллельные прямые. Решение задач
Параллельные прямые. Решение задач урок 1 и 2 (1)
урок 1 и 2 (1) Обеспечивающие подсистемы АИС. Математическое обеспечение
Обеспечивающие подсистемы АИС. Математическое обеспечение Аналоги теореми порівняння Колмогорова та їх застосування
Аналоги теореми порівняння Колмогорова та їх застосування Как можно заменить произведение равных сомножителей?
Как можно заменить произведение равных сомножителей? Многоранники
Многоранники