Содержание
- 2. Основные методы решений логарифмических уравнений
- 3. Определение Логарифмом положительного числа b по основанию a, где a>0, , называется показатель степени, в которую
- 4. 1. Использование определения логарифма.
- 5. 2. Метод потенцирования. Пример 2.
- 6. 3. Введение новой переменной. Пример 3.
- 7. 4. Приведение логарифмов к одному основанию.
- 8. 5. Метод логарифмирования.
- 9. 6.
- 10. Каждому уравнению поставьте в соответствие метод его решения * по определению логарифма метод потенцирования метод подстановки
- 11. Функциональные методы решения логарифмических уравнений *
- 12. Использование области допустимых значений уравнения
- 13. Определение Областью допустимых значений уравнения называется общая область определения всех функций, входящих в уравнение Утверждение1 Если
- 14. Утверждение 2. Если область допустимых значений уравнения состоит из конечного числа значений, то корни уравнения содержатся
- 15. Проверка: При х = -1 получаем 0=2. Равенство неверно. Значит х = -1 не является корнем
- 16. Алгоритм решения Находим ОДЗ уравнения. 2) Если ОДЗ - пустое множество, то уравнение не имеет корней.
- 17. Использование монотонности функций.
- 18. * Теорема. Если функция ƒ(х) монотонна на некотором промежутке , то уравнение ƒ(х) = c имеет
- 19. Теорема. Если на некотором промежутке функция ƒ(х) возрастает, а функция g(х) убывает, то уравнение ƒ(х) =
- 20. Алгоритм решения Найти ОДЗ. Подбором найти корень уравнения. С помощью монотонности функции доказать, что корень единственный.
- 21. Использование множества значений (ограниченности) функций
- 22. * f(x) и g(x)- элементарные функции, Е(f) и Е(g) – множества значений этих функций. Утверждение 1.
- 23. Утверждение 2. Если E(ƒ)∩E(g)= и f(x)≤ M, а g(x)≥M, то уравнение f(x)= g(x) равносильно системе уравнений
- 24. Алгоритм решения 1.Оценить обе части уравнения 2.Если f(x)≤ M, а g(x)≥M, то равенство f(x)= g(x) возможно
- 25. Проверьте свои знания тестированием Пройдите по ссылке: Логарифмические уравнения. Логарифмические уравнения.exe * Критерии оценки 3 б.
- 26. Ну кто придумал эту математику ! У меня всё получилось!!! Надо решить ещё пару примеров. Учитель
- 28. Скачать презентацию

























 Многоугольники (n-угольники)
Многоугольники (n-угольники) Презентация на тему Математические головоломки (3 класс)
Презентация на тему Математические головоломки (3 класс)  Решение задач к главе IV §1,2
Решение задач к главе IV §1,2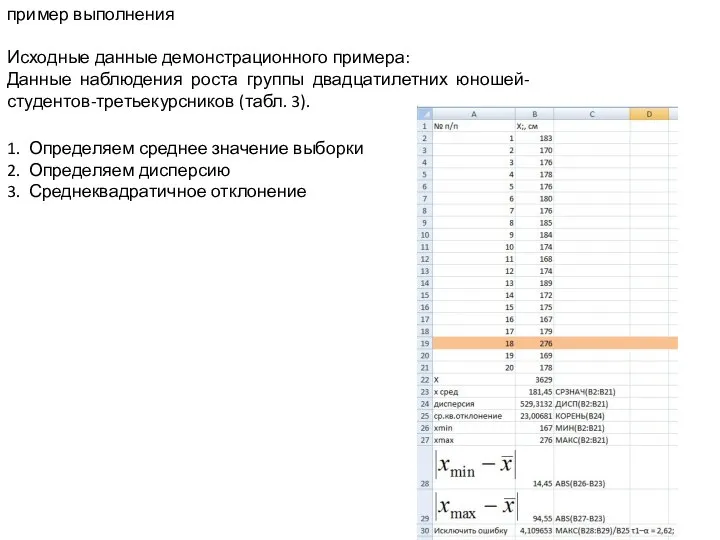 Данные наблюдения роста группы двадцатилетних юношей студентов
Данные наблюдения роста группы двадцатилетних юношей студентов Случаи сложения вида +7
Случаи сложения вида +7 Элементы нелинейного функционального анализа Глава 1. Дифференциальное исчисление в нормированных пространствах
Элементы нелинейного функционального анализа Глава 1. Дифференциальное исчисление в нормированных пространствах Значение переменных верного равенства. Корни уравнений
Значение переменных верного равенства. Корни уравнений Разработка обучающей программы по нахождению элементов треугольника
Разработка обучающей программы по нахождению элементов треугольника Наклонный круговой цилиндр
Наклонный круговой цилиндр Презентация на тему Свойства сложения (2 класс)
Презентация на тему Свойства сложения (2 класс)  Презентация на тему Площадь
Презентация на тему Площадь  Обыкновенные дроби
Обыкновенные дроби Синус, косинус и тангенс угла
Синус, косинус и тангенс угла Úsh perpendıkýlıar týraly teorema
Úsh perpendıkýlıar týraly teorema лекция3 (2)
лекция3 (2) perpendikulyarnost
perpendikulyarnost Компьютерное решение задач по теме Арифметическая прогрессия
Компьютерное решение задач по теме Арифметическая прогрессия Десятичные дроби
Десятичные дроби Что такое медиана?
Что такое медиана? Элементы нелинейного функционального анализа. Два способа задания атласа на сфере
Элементы нелинейного функционального анализа. Два способа задания атласа на сфере Применение подобия к доказательству теорем и решению задач. Урок 37
Применение подобия к доказательству теорем и решению задач. Урок 37 Многогранники. Тетраэдр
Многогранники. Тетраэдр Презентация на тему Внетабличное умножение и деление
Презентация на тему Внетабличное умножение и деление  Преобразование логарифмических выражений
Преобразование логарифмических выражений Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Математика. 3 класс
Математика. 3 класс Планирование эксперимента при проектировании РЭС
Планирование эксперимента при проектировании РЭС Презентация на тему СРАВНЕНИЕ ОТРЕЗКОВ И УГЛОВ
Презентация на тему СРАВНЕНИЕ ОТРЕЗКОВ И УГЛОВ