Содержание
- 2. 1. Алгебраические методы решения Если исходить из определения неравенства, в котором в обеих частях записаны выражения
- 3. 1.1. Сведение неравенства к равносильной системе или совокупности систем Как правило, преобразования используют для того, чтобы
- 4. В общем случае, если решение неравенства не укладывается в стандартную схему, ход решения разбивают на несколько
- 5. Пример 1. (МИОО, 2009). Решите неравенство Решение. Так как x2 - 6x + 9 = (x-3)2
- 6. при x = 2 или x = 4 . Значит, с учетом полученных ранее ограничений, x
- 7. На числовой прямой Ox дано графическое представление решения последнего неравенства. Замечание. При решении неравенства использован метод
- 8. Пример 2. (МИЭТ, 2000). Решите неравенство Решение. Выполняя равносильные преобразования данного неравенства, получим:
- 9. Неравенства, содержащие иррациональные выражения Приведем некоторые стандартные схемы для решения иррациональных неравенств, в которых используют возведение
- 12. Пример 3. Решите неравенство Решение. Если 2 - x > 0 или 2 - x =
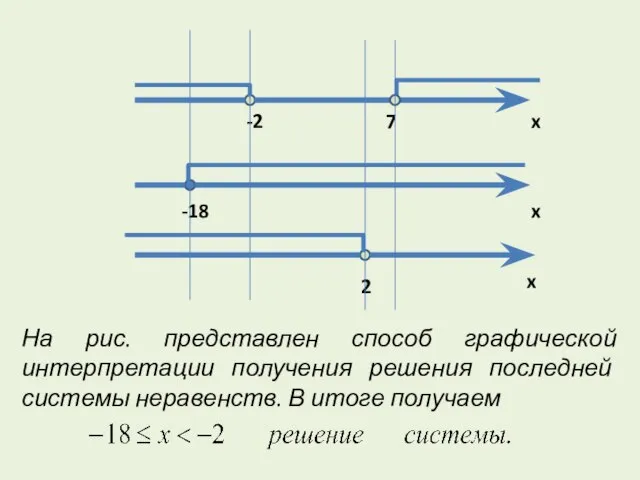
- 13. На рис. представлен способ графической интерпретации получения решения последней системы неравенств. В итоге получаем
- 14. Пример 4. (МИЭТ, 1999). Решите неравенство Решение. Используя схему (6), получим, что данное неравенство равносильно совокупности
- 15. Первое неравенство системы (I) приводим к виду: На числовой прямой Ox дано графическое представление решения первого
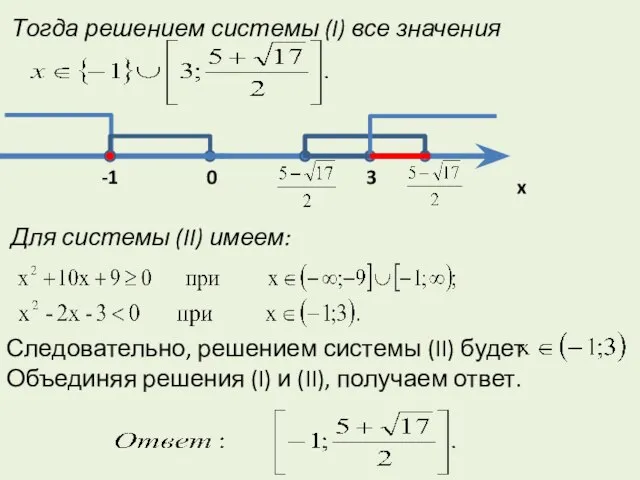
- 16. Тогда решением системы (I) все значения Для системы (II) имеем: Следовательно, решением системы (II) будет Объединяя
- 17. При решении данного в примере 4 неравенства использован формальный переход к равносильной совокупности по схеме (6).
- 18. Пусть x2-2x - 3
- 19. Пример 5. (МИОО, 2009). Решите неравенство Решение. Выполняя равносильные переходы, получим
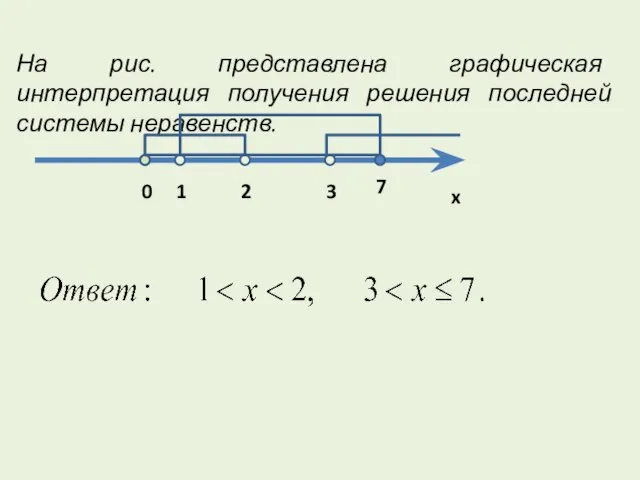
- 20. На рис. представлена графическая интерпретация получения решения последней системы неравенств.
- 21. Пример 6. Решите неравенство Решение. Обозначим . Тогда выразим x = t 2 + 2 и
- 22. Возвращаемся к переменной x :
- 23. Пример 7. (МИЭТ, 2002). Решите неравенство Решение. Область определения данного неравенства определяется условиями: Запишем исходное неравенство
- 24. Так как на области определения исходного неравенства , то, умножив обе части неравенства (*) на получим
- 25. На рис. представлена графическая интерпретация получения решения последней системы неравенств. С учетом условия - 0,5
- 26. Неравенства, содержащие показательные выражения Приведем некоторые стандартные схемы для решения показательных неравенств, в которых используют логарифмирование
- 27. В частности:
- 28. Пример 8. Решите неравенство Решение. 1-й способ. Область допустимых значений переменной x определяется условием: При допустимых
- 29. Получаем неравенство 2-й способ. Так как то, используя схему (12), получаем:
- 30. Замечание. При решении неравенства log2(x2-1) использована стандартная схема решения логарифмических неравенств (см. раздел неравенства, содержащие логарифмические
- 31. Пример 9. Решите неравенство (x2 + x +1)x Решение. Приведем неравенство к виду (x2 + x
- 32. При решении данного неравенства использован формальный переход к равносильной совокупности по схеме (9). Рассмотрим содержательную сторону
- 34. Неравенства, содержащие логарифмические выражения Приведем некоторые стандартные схемы для решения логарифмических неравенств, в которых используют потенцирование
- 35. ● Если число 0 В частности: ● Если число a >1, то ● Если число 0
- 36. Пример 10. Решите неравенство log0.1(x2+x-2)>log0.1(x+3) Решение. Так как основание 0,1 логарифмов, стоящих в обеих частях неравенства,
- 37. Пример 11. (МИОО, 2009). Решите неравенство Решение. Выполняя равносильные переходы, получим, что данное неравенство равносильно следующей
- 38. На рис. представлена графическая интерпретация получения решения последней системы неравенств.
- 39. Пример 12. (ЕГЭ 2010). Решите неравенство Решение. В соответствии с определением логарифма, входящие в неравенство выражения
- 40. Так как при допустимых значениях переменной x по свойствам логарифма справедливы равенства: то исходное неравенство приводится
- 41. С учетом области определения данного неравенства получаем ответ.
- 42. Неравенства, содержащие выражения с модулями Пример 13. (МИЭТ, 2002). Решите неравенство Решение. Данное неравенство равносильно совокупности
- 44. Приведем некоторые стандартные схемы для решения неравенств с модулями, которые опираются на определение модуля, его геометрический
- 45. Пример 14. Решите неравенство Решение. Используя схему (20) получаем, что данное неравенство равносильно системе неравенств или
- 46. Пример 15. Решите неравенство Решение. Данное неравенство равносильно следующему Используя схему (23), получаем, что это неравенство,
- 47. Пример 16. Решите неравенство Решение. Используя схему (22), получаем, что данное неравенство равносильно совокупности неравенств Используя
- 48. Для решения неравенств вида: где символ \/ заменяет один из знаков неравенств: применяют метод промежутков. Для
- 49. На каждом из промежутков, на которые найденные точки разбивают ОДЗ, функции, стоящие под знаком модуля, имеют
- 50. Освобождаясь от знаков модулей, с учетом знаков выражений под знаком модуля решим данное неравенство на каждом
- 51. Если , то исходное неравенство равносильно неравенству x -1+ x - 2 > 3+ x ,
- 52. Расщепление неравенств Если левая часть неравенства представляет собой произведение двух выражений, а правая часть равна нулю,
- 54. Пример 18. Решите неравенство Решение. Приведем данное неравенство к следующему виду: В соответствии со схемой полученное
- 55. Решим каждое неравенство системы (I). Для неравенства (1) имеем: Для неравенства (2) имеем:
- 56. Значит все значения x принадлежат (0; 1] – решения системы (I). Найдем решение системы (II). Для
- 57. Значит все значения – решения системы (II). Объединяя решения систем (I) и (II), получаем ответ. Для
- 59. Скачать презентацию








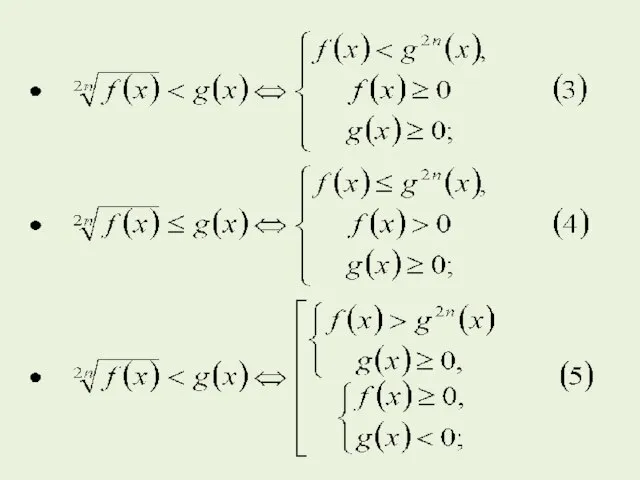
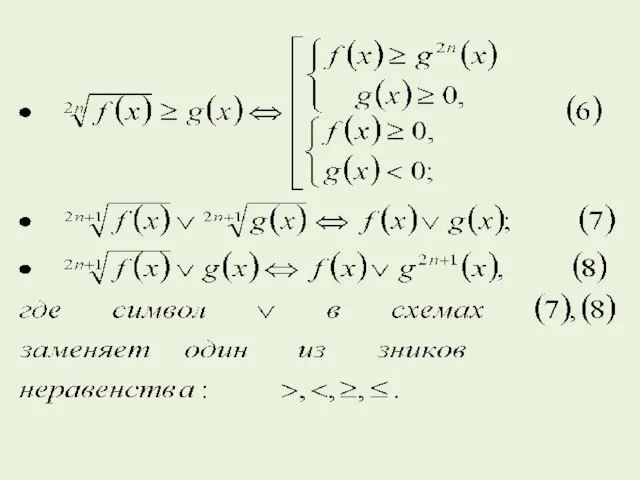












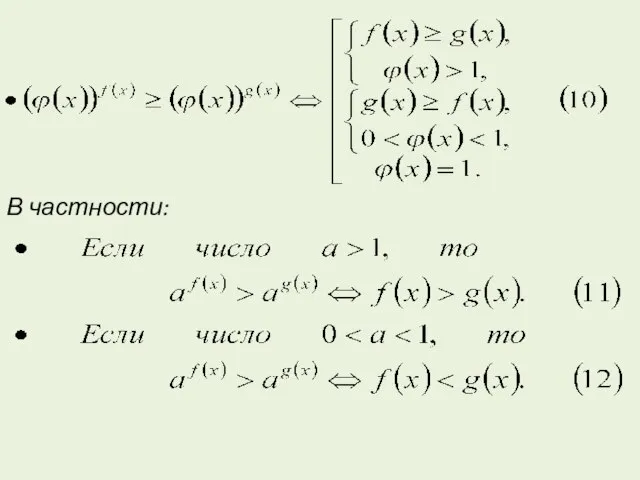





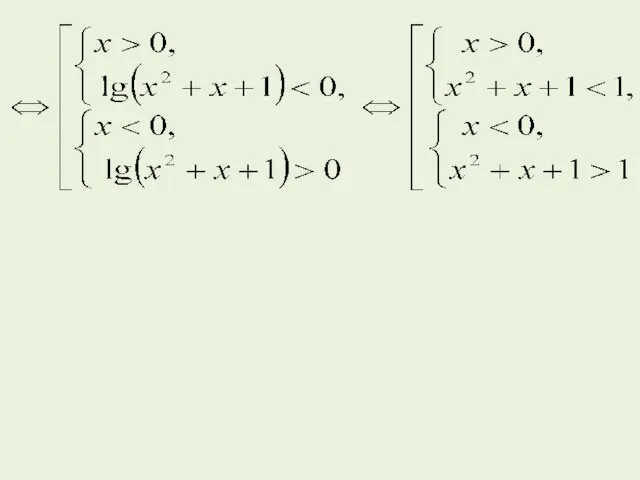









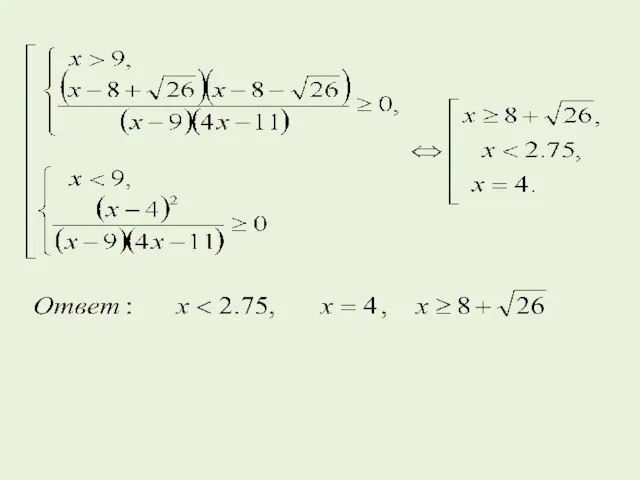









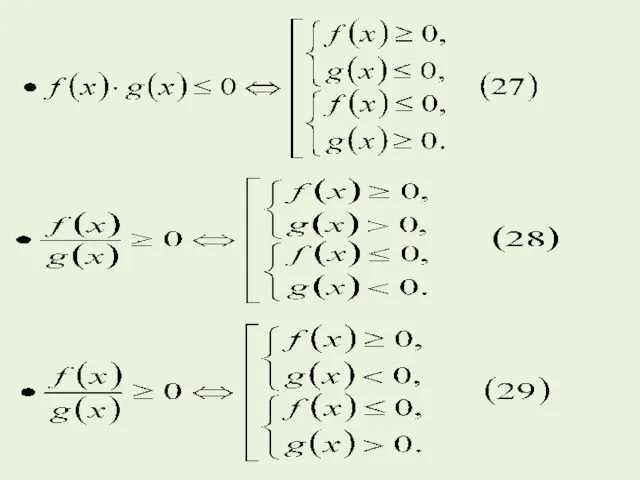


![Значит все значения x принадлежат (0; 1] – решения системы (I). Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/285644/slide-55.jpg)

 Строение функции, свойства, графики
Строение функции, свойства, графики Интерактивный тренажёр. 4 класс
Интерактивный тренажёр. 4 класс Проверка умножения делением
Проверка умножения делением Монотонность функции
Монотонность функции Таблица умножения в пределах 100. Урок повторения и закрепления
Таблица умножения в пределах 100. Урок повторения и закрепления Волшебный мир иллюзий
Волшебный мир иллюзий Презентация на тему Слагаемые Сумма
Презентация на тему Слагаемые Сумма  Определение степени с целым отрицательным показателем
Определение степени с целым отрицательным показателем ГИА - 2016. Открытый банк заданий по математике. Задача №15
ГИА - 2016. Открытый банк заданий по математике. Задача №15 Презентация на тему Квадратный сантиметр (3 класс)
Презентация на тему Квадратный сантиметр (3 класс) 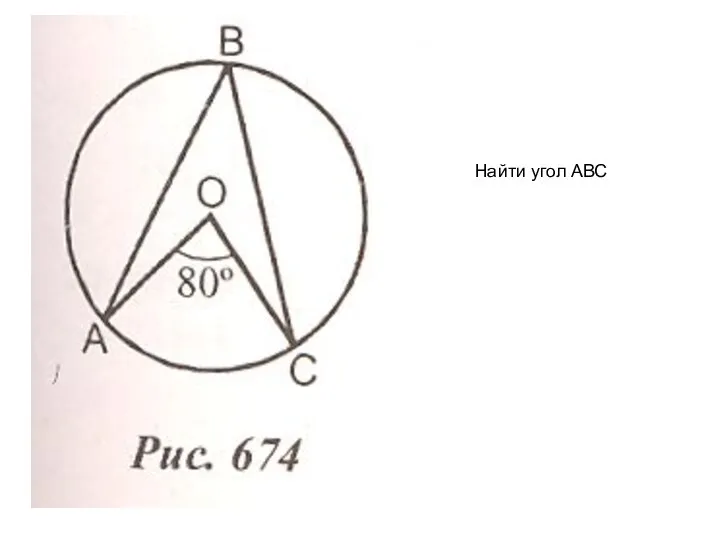 Найти угол АВС
Найти угол АВС Элементы комбинаторики
Элементы комбинаторики Практикум по решению комбинированных уравнений
Практикум по решению комбинированных уравнений Пирамида. Построение правильной треугольной пирамиды
Пирамида. Построение правильной треугольной пирамиды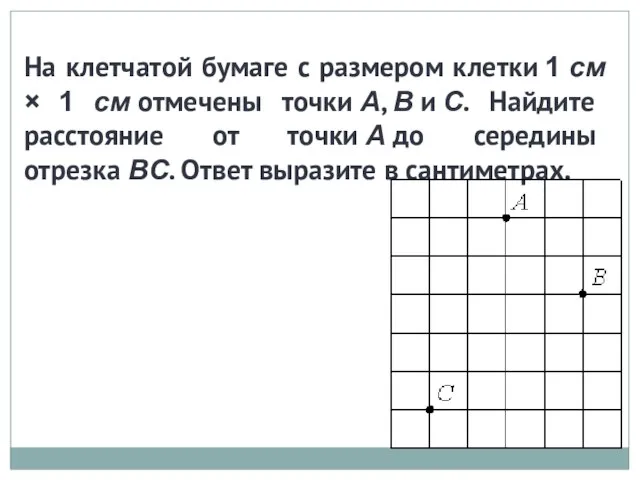 Решение задач
Решение задач МОУ Гимназия имени академика Н.Г. Басова при Воронежском госуниверситете Белоусова Алла Генриховна, учитель математики, кандид
МОУ Гимназия имени академика Н.Г. Басова при Воронежском госуниверситете Белоусова Алла Генриховна, учитель математики, кандид Треугольники. Задача
Треугольники. Задача Приложения скалярного произведения
Приложения скалярного произведения Планы второго порядка
Планы второго порядка Параллелограмм и трапеция
Параллелограмм и трапеция Математика звука
Математика звука Elemente de teoria reziduurilor
Elemente de teoria reziduurilor Многогранники. Тела Архимеда
Многогранники. Тела Архимеда Системы уравнений. Основные понятия
Системы уравнений. Основные понятия Презентация на тему Прибавление и вычитание числа 3
Презентация на тему Прибавление и вычитание числа 3  Решение задач
Решение задач Функцияның нүктедегі шегі туралы ұғым және функцияның үзіліссіздігі
Функцияның нүктедегі шегі туралы ұғым және функцияның үзіліссіздігі Прямоугольный параллелепипед. Урок обобщения и систематизации знаний
Прямоугольный параллелепипед. Урок обобщения и систематизации знаний