Содержание
- 2. План урока Осевая симметрия Центральная симметрия Практическая работа Понятие отображения плоскости на себя Понятие движения Решение
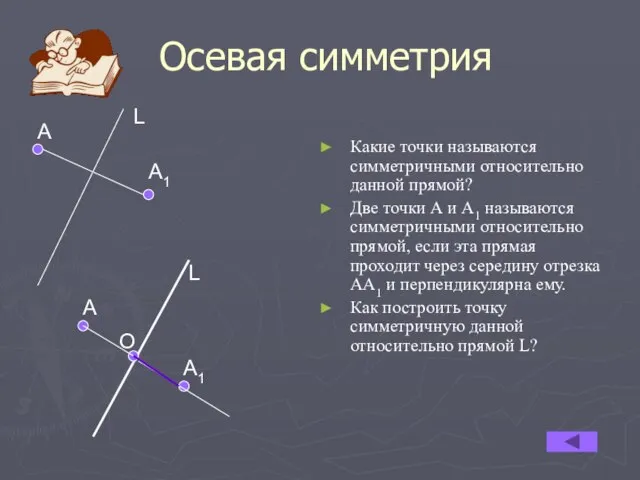
- 3. Осевая симметрия Какие точки называются симметричными относительно данной прямой? Две точки А и А1 называются симметричными
- 4. Центральная симметрия Какие точки называются симметричными относительно данной точки? Две точки А и А1 называются симметричными
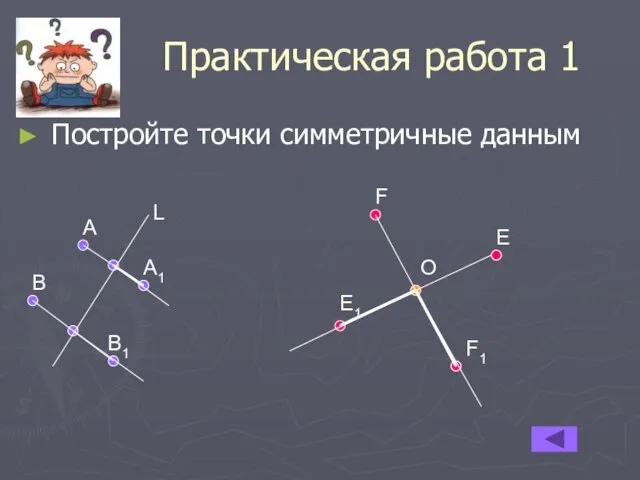
- 5. Практическая работа 1 Постройте точки симметричные данным А В А1 В1 L F E O E1
- 6. Отображение плоскости на себя Пусть каждой точке плоскости ставится в соответствие какая –то точка этой плоскости,
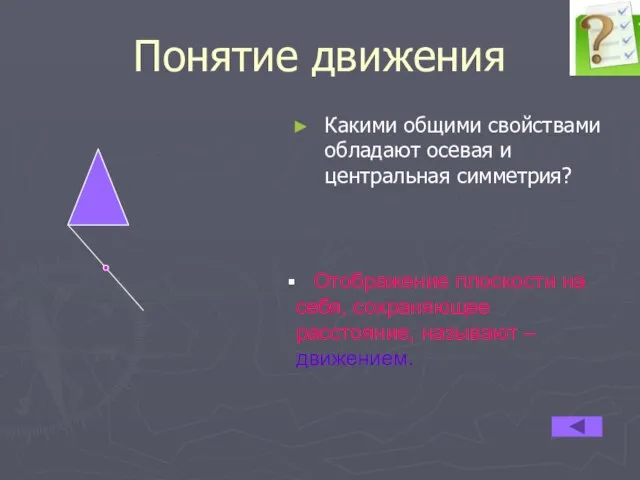
- 7. Понятие движения Какими общими свойствами обладают осевая и центральная симметрия? Отображение плоскости на себя, сохраняющее расстояние,
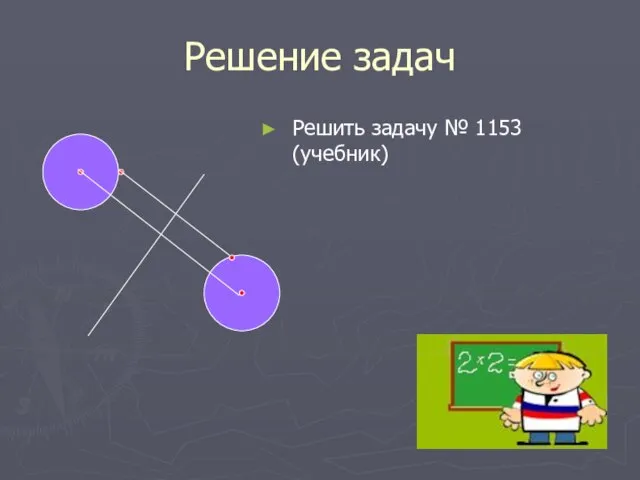
- 8. Решение задач Решить задачу № 1153 (учебник)
- 9. Итог урока Осевая и центральная симметрия - движение. Д/з п.113,114 вопросы 1 -6 № 1148(а)
- 12. Скачать презентацию




 Числовые последовательности
Числовые последовательности Презентация на тему Тренажер по математике 2 класс
Презентация на тему Тренажер по математике 2 класс  Уравнение сферы
Уравнение сферы Задачи на готовых чертежах по теме Подобие
Задачи на готовых чертежах по теме Подобие Площади. Теорема Пифагора. Урок - зачёт 8 класс
Площади. Теорема Пифагора. Урок - зачёт 8 класс Интеграл
Интеграл По следам теоремы Пифагора
По следам теоремы Пифагора Математика в мире животных и животные в математике
Математика в мире животных и животные в математике Тела вращения в природе
Тела вращения в природе Перпендикулярность плоскостей
Перпендикулярность плоскостей Дифуры 1 порядка
Дифуры 1 порядка Нематематики о математике
Нематематики о математике Ортогональная проекция плоской фигуры на плоскость и ее площадь
Ортогональная проекция плоской фигуры на плоскость и ее площадь Письменное умножение трёхзначного числа на однозначное
Письменное умножение трёхзначного числа на однозначное Деление окружности на 5 равных частей. Сопряжение
Деление окружности на 5 равных частей. Сопряжение Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Решение уравнений с одной переменной
Решение уравнений с одной переменной Правильные многогранникик
Правильные многогранникик Признаки равенства треугольников
Признаки равенства треугольников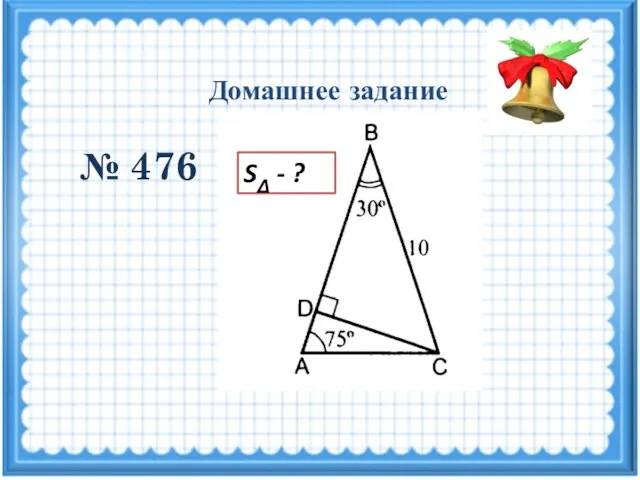 Домашнее задание № 476
Домашнее задание № 476 Сумма углов треугольника
Сумма углов треугольника Комбинаторика. Факториал. Вычисление факториала. Формула числа перестановок, размещений и сочетаний
Комбинаторика. Факториал. Вычисление факториала. Формула числа перестановок, размещений и сочетаний Презентация на тему Решение квадратных уравнений и неравенств
Презентация на тему Решение квадратных уравнений и неравенств  Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной
Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной Средняя линия треугольника
Средняя линия треугольника Презентация на тему КВН. Математика повсюду
Презентация на тему КВН. Математика повсюду  Корень уравнения
Корень уравнения Задачи на проценты. ОГЭ
Задачи на проценты. ОГЭ