Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной

Цели обучения:
6.2.2.14
решать системы линейных неравенств с одной переменной;

Критерии оценивания
Учащиеся
знают:
как решать системы линейных неравенств с одной переменной
как записывать, используя математическую символику, ответы к решениям систем неравенств;
умеют
решать системы линейных неравенств с одной переменной
изображать решения систем неравенств на координатной прямой;
записывать решения систем неравенств в виде числового промежутка и записывать заданный числовой промежуток в виде неравенства.

Найти пересечение множеств [-3; 2]∩(0; 7)
[-3; 2]∩(0; 7)
= (0;2]
Системы линейных неравенств

[-3; 2]∩(0; 7)
может быть задано
аналитически:
Несколько неравенств с одной переменной образуют систему неравенств, если ставится задача найти все общие решения заданных неравенств.
Пересечение множеств
Системы линейных неравенств

Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называют решением системы неравенств.
Определение:
Системы линейных неравенств

Определение:
Множество всех решений системы неравенств представляет собой общее решение системы неравенств.
(0;2]
Системы линейных неравенств

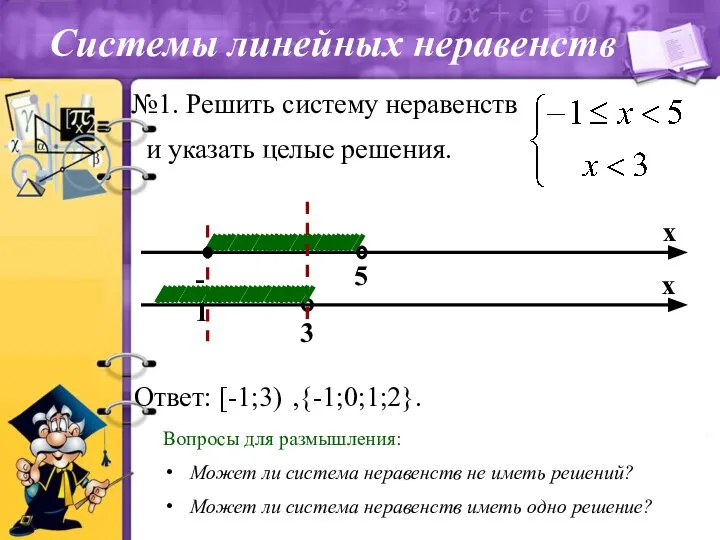
и указать целые решения.
Вопросы для размышления:
Может ли система неравенств не иметь решений?
Может ли система неравенств иметь одно решение?
Ответ: [-1;3)
,{-1;0;1;2}.
№1. Решить систему неравенств
Системы линейных неравенств

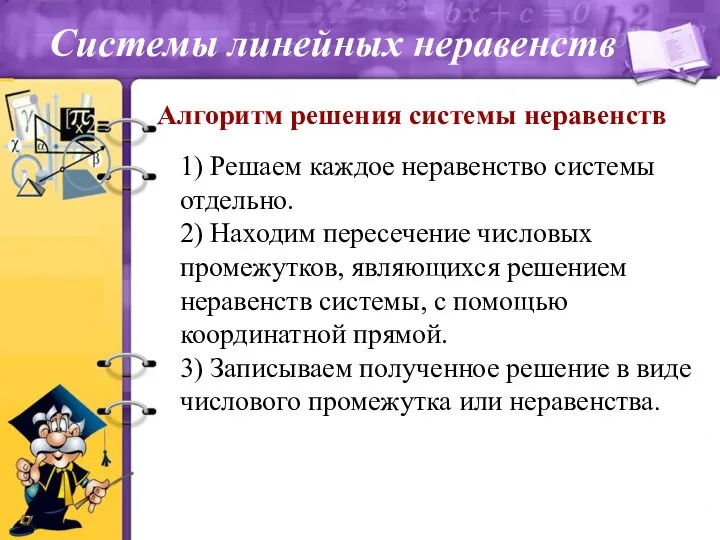
Алгоритм решения системы неравенств
1) Решаем каждое неравенство системы отдельно.
2) Находим пересечение числовых промежутков, являющихся решением неравенств системы, с помощью координатной прямой.
3) Записываем полученное решение в виде числового промежутка или неравенства.
Системы линейных неравенств