Содержание
- 2. Дифференциальные уравнения. Определение решения При решении различных задач математики, физики, химии и других наук часто пользуются
- 3. Задачи, приводящие к дифференциальным уравнениям
- 4. Другие задачи
- 5. Дифференциальные уравнения первого порядка. Основные понятия
- 7. Дифференциальное уравнение первого порядка. Основные понятия
- 8. Уравнения с разделяющимися переменными
- 13. Линейные уравнения
- 19. Метод вариации постоянной
- 20. Метод вариации постоянной
- 21. Метод вариации постоянной
- 22. Метод вариации постоянной
- 23. Метод вариации постоянной
- 24. Метод вариации постоянной
- 25. Метод вариации постоянной
- 29. Уравнение Бернулли
- 32. Уравнение в полных дифференциалах
- 34. Скачать презентацию































 Треугольные узоры. Правильный треугольник
Треугольные узоры. Правильный треугольник Сложение и вычитание числа 2
Сложение и вычитание числа 2 История числа 1
История числа 1 Открытый банк заданий ЕГЭ по математике
Открытый банк заданий ЕГЭ по математике Прямая. Ортогональные проекции прямой линии
Прямая. Ортогональные проекции прямой линии Презентация на тему Равнобедренный треугольник, признаки равенства треугольников
Презентация на тему Равнобедренный треугольник, признаки равенства треугольников  Вписанная и описанная окружность
Вписанная и описанная окружность Метод Гаусса
Метод Гаусса Числовые и буквенные выражения. (5 класс)
Числовые и буквенные выражения. (5 класс) Математические структуры
Математические структуры Устный счет. 6 класс
Устный счет. 6 класс Презентация на тему Числовые неравенства и их свойства
Презентация на тему Числовые неравенства и их свойства  КВН Знакомьтесь: геометрия
КВН Знакомьтесь: геометрия Натуральные числа. Тест по математике для учащихся
Натуральные числа. Тест по математике для учащихся Единицы времени
Единицы времени Решение уравнений, содержащих параметры
Решение уравнений, содержащих параметры Деление плоскости на 9 частей
Деление плоскости на 9 частей Ряды Фурье
Ряды Фурье Метод Зейделя
Метод Зейделя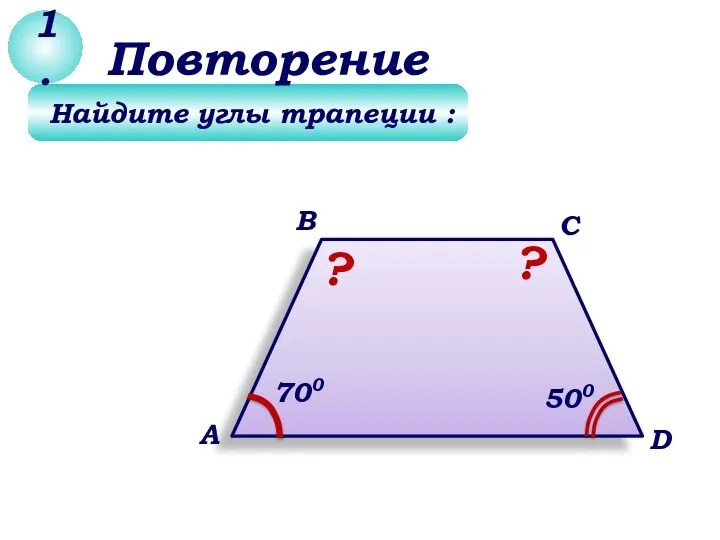 Задачи по геометрия 8 класс
Задачи по геометрия 8 класс Описание линейной дискретной системы в частотной области (ЛДС). Частотные характеристики ЛДС
Описание линейной дискретной системы в частотной области (ЛДС). Частотные характеристики ЛДС Решение неравенств. ЕГЭ, задание 15
Решение неравенств. ЕГЭ, задание 15 Учимся писать цифры
Учимся писать цифры Иррациональные уравнения. Основы школьного курса математики
Иррациональные уравнения. Основы школьного курса математики Урок-игра. Аукцион математических знаний
Урок-игра. Аукцион математических знаний Нормальные формы булевых функций
Нормальные формы булевых функций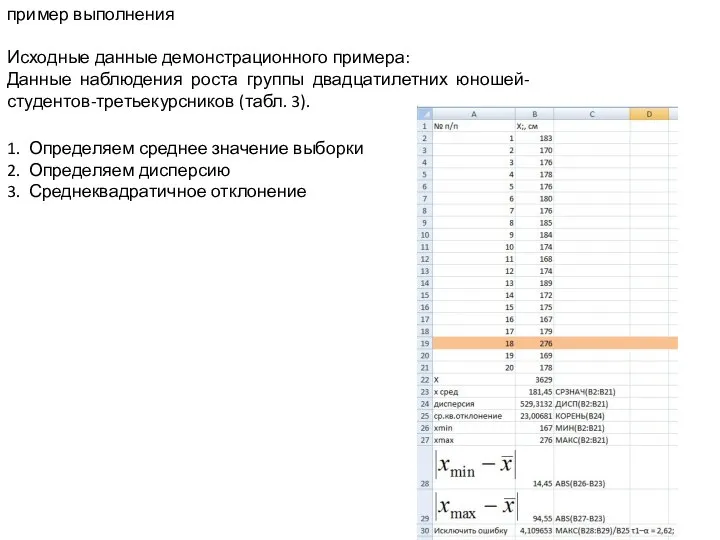 Данные наблюдения роста группы двадцатилетних юношей студентов
Данные наблюдения роста группы двадцатилетних юношей студентов Время и работа. Связь между величинами
Время и работа. Связь между величинами