Содержание
- 2. Замена переменной: универсальная тригонометрическая подстановка
- 3. Тогда Следовательно
- 4. Пример. Вычислить интеграл:
- 5. Решение:
- 6. 2 Если выражение R(sin x,cos x) при замене sin x на (-sin x) только меняет знак,
- 7. Пример. Вычислить интеграл:
- 8. Решение: Следовательно, можно применять рекомендуемую подстановку:
- 10. 3 Если выражение R(sin x,cos x) при замене cos x на (-cos x) только меняет знак,
- 11. Пример. Вычислить интеграл:
- 12. Решение: Следовательно, можно применять рекомендуемую подстановку:
- 14. 4 Интегралы вида где α и β – действительные числа, вычисляются с помощью формул, преобразующих произведение
- 15. Формулы преобразования:
- 16. Пример. Вычислить интеграл:
- 18. Скачать презентацию











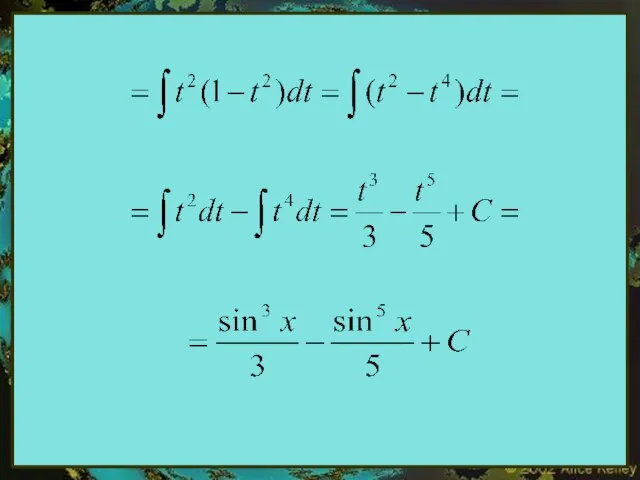



 Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Методичні основи вивчення часу і одиниць його вимірювання
Методичні основи вивчення часу і одиниць його вимірювання Алгебра событий
Алгебра событий Возрастание и убывание функций. Экстремумы
Возрастание и убывание функций. Экстремумы Решение однородных тригонометрических уравнений
Решение однородных тригонометрических уравнений Десятичные дроби. Колесо истории
Десятичные дроби. Колесо истории Сводка и группировка
Сводка и группировка Сложение и вычитание вида ±1
Сложение и вычитание вида ±1 Алгоритм метода конечных элементов (МКЭ)
Алгоритм метода конечных элементов (МКЭ) Нахождение дроби от числа
Нахождение дроби от числа Таблица сложения чисел с переходом через десяток. Тренажёр
Таблица сложения чисел с переходом через десяток. Тренажёр Интеграл. Первообразная
Интеграл. Первообразная Случаи вычитания 11-
Случаи вычитания 11- Дроби вокруг нас
Дроби вокруг нас Повторение пройденного (1 класс)
Повторение пройденного (1 класс) Квадратичная функция. Преобразование графика параболы путем параллельного переноса вдоль осей абцисс и ординат
Квадратичная функция. Преобразование графика параболы путем параллельного переноса вдоль осей абцисс и ординат Переводчицы. Задача
Переводчицы. Задача Сложение и вычитание числа 2
Сложение и вычитание числа 2 Задания по геометрии
Задания по геометрии Час. Минута
Час. Минута Алгоритмы направленного перебора
Алгоритмы направленного перебора Понятие множества
Понятие множества Презентация на тему Алгебра и начала математического анализа
Презентация на тему Алгебра и начала математического анализа  Тела вращения
Тела вращения Векторы в пространстве
Векторы в пространстве Элементы векторной алгебры
Элементы векторной алгебры Интерполяционный многочлен Ньютона
Интерполяционный многочлен Ньютона Тренажёр. Таблица умножения
Тренажёр. Таблица умножения