Содержание
- 2. Основные понятия Комплексным числом z называют выражение: где а и b – действительные числа, i –
- 3. Геометрическое изображение комплексных чисел Плоскость, на которой изображаются комплексные числа, называют плоскостью комплексной переменной. A(a; b)
- 4. Тригонометрическая форма записи комплексных чисел Тогда имеют место равенства: Следовательно, комплексное число z можно представить в
- 5. Действия над комплексными числами Равенство комплексных чисел. 1 2 Сложение и вычитание комплексных чисел.
- 6. Действия над комплексными числами 3 Умножение комплексных чисел. Сложение и вычитание комплексных чисел, изображенных векторами производится
- 7. Действия над комплексными числами На основании этого правила получим: тогда произведение находится по формуле: Если комплексные
- 8. Действия над комплексными числами 4 Деление комплексных чисел. Если комплексные числа заданы в тригонометрической форме:
- 9. Действия над комплексными числами Найти произведение и частное комплексных чисел:
- 10. Действия над комплексными числами 5 Возведение в степень комплексного числа. 6 Извлечение корня из комплексного числа.
- 11. Действия над комплексными числами Придавая k значения 0, 1, 2, …,n –1, получим n различных значений
- 12. Действия над комплексными числами Найти все значения кубического корня из единицы A В С
- 13. Показательная форма комплексного числа Рассмотрим показательную функцию от комплексной переменной z. Комплексные значения функции w определяются
- 14. Показательная форма комплексного числа Если в формуле (1) положим x = 0, то получим: Эта формула
- 16. Скачать презентацию













 Решение задач по теме Смежные и вертикальные углы. Перпендикулярные прямые
Решение задач по теме Смежные и вертикальные углы. Перпендикулярные прямые Координатная плоскость
Координатная плоскость Таблица сложения
Таблица сложения Теория о трех перпендикулярах
Теория о трех перпендикулярах Решение задач на межпредметные связи
Решение задач на межпредметные связи 764fab9c-7974-40e4-8362-2c4469fed7e2
764fab9c-7974-40e4-8362-2c4469fed7e2 Презентация на тему Умножение и деление на 10 и 100
Презентация на тему Умножение и деление на 10 и 100 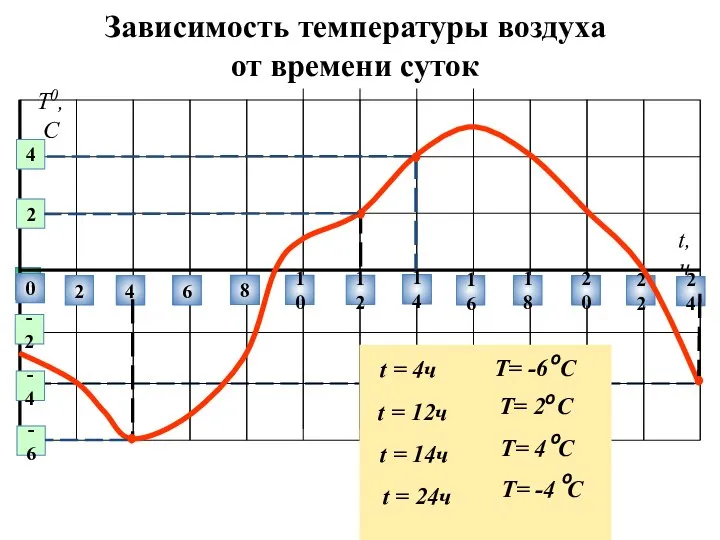 Зависимость температуры воздуха от времени суток
Зависимость температуры воздуха от времени суток Математическая тревожность
Математическая тревожность Цифра 10
Цифра 10 Логарифмические уравнения и их системы
Логарифмические уравнения и их системы Простейшие дифференциальные уравнения 2 порядка
Простейшие дифференциальные уравнения 2 порядка funktsia_svoystva_funktsii
funktsia_svoystva_funktsii Практическое применение теоремы косинусов и синусов. 9 класс
Практическое применение теоремы косинусов и синусов. 9 класс Логарифмическая функция
Логарифмическая функция Параллельные прямые
Параллельные прямые Умножаем и делим на 5
Умножаем и делим на 5 Пирамида. Египетские пирамиды
Пирамида. Египетские пирамиды Презентация на тему Уравнения в ЕГЭ по математике: примеры и решения
Презентация на тему Уравнения в ЕГЭ по математике: примеры и решения  Осевая симметрия
Осевая симметрия Решение задач на временные отношения (подготовка к олимпиаде по математике обучающихся 4 класса)
Решение задач на временные отношения (подготовка к олимпиаде по математике обучающихся 4 класса) Решение задач по теме Соотношения между сторонами и углами в прямоугольном треугольнике
Решение задач по теме Соотношения между сторонами и углами в прямоугольном треугольнике Квадрат та його властивості
Квадрат та його властивості Свойства логарифмов
Свойства логарифмов Презентация на тему Формулы сокращённого умножения
Презентация на тему Формулы сокращённого умножения  Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Многогранники
Многогранники Презентация на тему Кто хочет стать математиком
Презентация на тему Кто хочет стать математиком