Содержание
- 2. Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому
- 3. Представление левой части неравенства в виде суммы неотрицательных слагаемых (правая часть равна 0) с использованием тождеств.
- 4. для любых действительных х и у Пример 2. Доказать, что для любых x и y Доказательство.
- 5. 2. Метод от противного Вот хороший пример применения данного метода. Доказать, что для a, b ϵ
- 6. Пример 5. Доказать, что для любых чисел А,В,С справедливо неравенство Доказательство. Очевидно, что данное неравенство достаточно
- 7. Пусть теперь нашлись такие неотрицательные числа А, В и С, для которых выполняется неравенство , что
- 8. для хϵR для хϵR Использование свойств квадратного трехчлена Метод основан на свойстве неотрицательности квадратного трехчлена ,
- 9. для хϵR Пример 7. Доказать, что для любых действительных х и у имеет место быть неравенство
- 10. Пример 8. Доказать, что для любых действительных значениях х и у. Доказательство. Пусть , Это означает,
- 11. Метод введения новых переменных или метод подстановки Пример 9. Доказать, что для любых неотрицательных чисел х,
- 12. для аϵR Использование свойств функций. Пример 10. Докажем неравенство для любых а и b. Доказательство. Рассмотрим
- 13. Пример 11. Докажем, что для любых Доказательство. на R. Если , то знаки чисел и совпадают,
- 14. Применение метода математической индукции Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12. Доказать,
- 15. *3 3) Докажем истинность утверждения при n=k+1. Сравним и : , Имеем: Вывод: утверждение верно для
- 16. Использование замечательных неравенств Теорема о средних (неравенство Коши) Неравенство Коши – Буняковского Неравенство Бернулли Рассмотрим каждое
- 17. Применение теоремы о средних (неравенства Коши) Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего
- 18. Пусть n=2, , , тогда Пусть n=2, a>0, тогда Пусть n=3, , , , тогда Пример
- 19. Неравенство Коши - Буняковского Неравенство Коши - Буняковского утверждает, что для любых ; справедливо соотношение Доказанное
- 20. Пример 14. Доказать, что для любых a,b,c ϵ R справедливо неравенство Доказательство. Запишем исследуемое неравенство в
- 21. Неравенство Бернулли Неравенство Бернулли утверждает, что если х>-1, то для всех натуральных значений n выполняется неравенство
- 22. Пример 16. Доказать, что для любых n ϵ N Доказательство. Положив х=0,5 и применив теорему Бернулли
- 24. Скачать презентацию





















 Презентация на тему Окружность, ее центр и радиус
Презентация на тему Окружность, ее центр и радиус  Вектор. Равенство векторов
Вектор. Равенство векторов Степень, графики функций, пропорции на уроках математики и физики
Степень, графики функций, пропорции на уроках математики и физики Связь деления и умножения
Связь деления и умножения Интегрирование некоторых классов функций. Лекция 2
Интегрирование некоторых классов функций. Лекция 2 Сравнение, сложение и вычитание дробей с разными знаменателями
Сравнение, сложение и вычитание дробей с разными знаменателями Математика. 1 класс
Математика. 1 класс Построение графиков функций
Построение графиков функций Площадь фигур
Площадь фигур Уравнение. Правила решения уравнения
Уравнение. Правила решения уравнения Умножение смешанных дробей
Умножение смешанных дробей Площадь геометрических фигур. Задачи
Площадь геометрических фигур. Задачи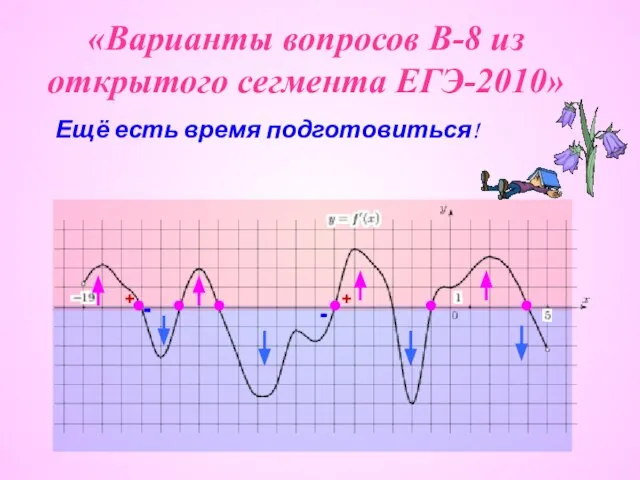 Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Критерий Пирсона
Критерий Пирсона Формулы сложения. Тригонометрические формулы
Формулы сложения. Тригонометрические формулы Анализ ошибок. Параллелепипеды. 10 класс
Анализ ошибок. Параллелепипеды. 10 класс Практическая работа
Практическая работа Построение таблиц истинности для логических выражений
Построение таблиц истинности для логических выражений Круг, окружность, длина и площадь окружности
Круг, окружность, длина и площадь окружности Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира Вычисли и запомни
Вычисли и запомни Площадь треугольника
Площадь треугольника Применение производной функции для отыскания точек экстремума
Применение производной функции для отыскания точек экстремума Проценты. Часть 2
Проценты. Часть 2 Площадь полной поверхности призмы
Площадь полной поверхности призмы Косинус острого угла прямоугольного треугольника
Косинус острого угла прямоугольного треугольника Пирамида
Пирамида Как посчитать консонанс
Как посчитать консонанс