Содержание
- 2. Одной из основных задач, возникающих при исследовании функции, является нахождение промежутков монотонности функции (промежутков возрастания и
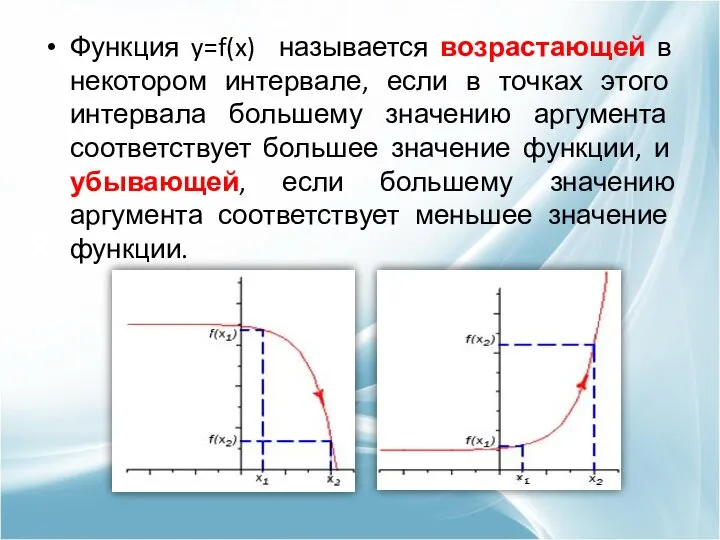
- 3. Функция y=f(x) называется возрастающей в некотором интервале, если в точках этого интервала большему значению аргумента соответствует
- 4. возрастающая убывающая убывающая убывающая возрастающая возрастающая и убывающая на интервалах возрастающая и убывающая на интервалах возрастающая
- 5. Если дифференцируемая функция y=f(x) возрастает (убывает) в данном интервале, то производная этой функции не отрицательна (не
- 6. Если производная функции y=f(x) положительна (отрицательна) на некотором интервале, то функция в этом интервале монотонно возрастает
- 7. Находим область определения функции f(x). Вычисляем производную f’(x) данной функции. Находим точки, в которых f’(x)=0 или
- 8. Область определения: R. Функция непрерывна. Вычисляем производную : y’=6x²-6x-36. Находим критические точки: y’=0. x²-x-6=0 Д=1-4*(-6)*1=1+24=25 Делим
- 9. Область определения: R. Функция непрерывна. Вычисляем производную : y’=3x²-6x. Находим критические точки: y’=0. x²-2x=0 x(x-2)=0 x1=0
- 10. Точку x=x0 называют точкой минимума функции y=f(x), если у этой точки существует окрестность, для всех точек
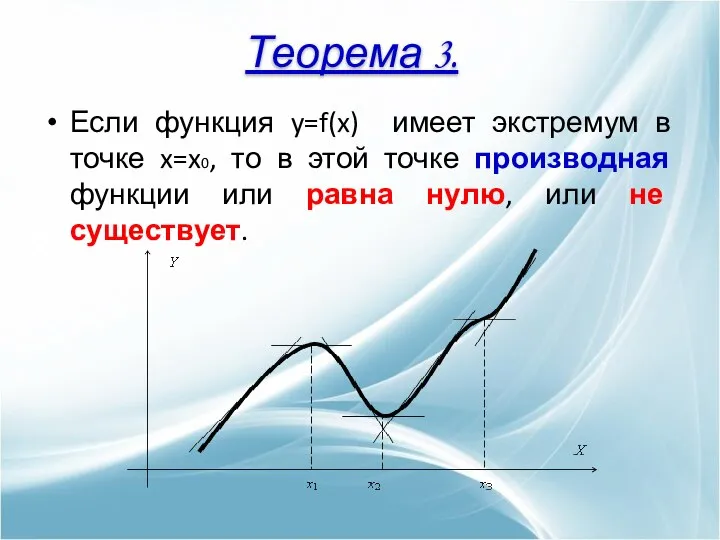
- 11. Если функция y=f(x) имеет экстремум в точке x=x0, то в этой точке производная функции или равна
- 12. Если производная f’(x) при переходе через точку x0 меняет знак, то точка x0 является точкой экстремума
- 13. Область определения: R. Функция непрерывна. Вычисляем производную : y’=-6x²-6x+12. Находим критические точки: y’=0. -x²-x+2=0 Д=1-4*(-1)*2=1+8=9 x1=1;
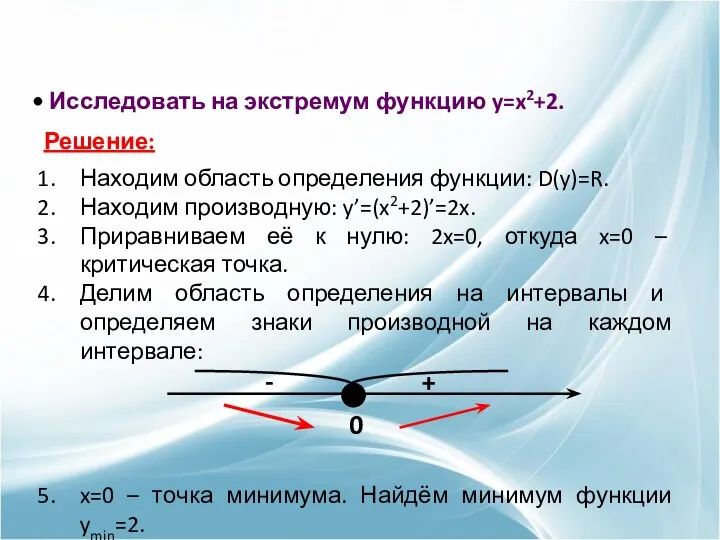
- 14. Исследовать на экстремум функцию y=x2+2. Решение: Находим область определения функции: D(y)=R. Находим производную: y’=(x2+2)’=2x. Приравниваем её
- 15. Исследовать на экстремум функцию y=x3+3x2+9x-6. Решение: Находим область определения функции: D(y)=R. Находим производную: y’=(x3+3x2+9x-6)’=3x2+6x+9. Приравниваем её
- 17. Скачать презентацию










 Некоторые законы распределения случайных величин. Нормальный закон распределения (закон Гаусса)
Некоторые законы распределения случайных величин. Нормальный закон распределения (закон Гаусса) Математика. Занятие 31
Математика. Занятие 31 Подобные треугольники. (8 класс)
Подобные треугольники. (8 класс) Числа 6 и 7. Письмо цифры 7 (1 класс)
Числа 6 и 7. Письмо цифры 7 (1 класс) Эквивалентные преобразования формул
Эквивалентные преобразования формул Численные методы решения систем линейных уравнений
Численные методы решения систем линейных уравнений Косинусоида. Задание № 9
Косинусоида. Задание № 9 Проценты. ОГЭ и ЕГЭ
Проценты. ОГЭ и ЕГЭ Треугольники. Задачи
Треугольники. Задачи Решение СЛАУ методом Крамера
Решение СЛАУ методом Крамера Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Устный счёт для дошкольников
Устный счёт для дошкольников Десятичные дроби произвольного знака
Десятичные дроби произвольного знака Вычитание смешанных чисел. 5 класс
Вычитание смешанных чисел. 5 класс Арифметический пейзаж
Арифметический пейзаж электронный учебник по интеллектике в 5 классе. знакомство с вероятностью
электронный учебник по интеллектике в 5 классе. знакомство с вероятностью Приближенные решения уравнений
Приближенные решения уравнений Цикл for
Цикл for Вторая производная и её физический смысл
Вторая производная и её физический смысл Max cut problem
Max cut problem Третий признак равенства треугольников. 7 класс
Третий признак равенства треугольников. 7 класс Тригонометрия (В5, В7) на ЕГЭ
Тригонометрия (В5, В7) на ЕГЭ Играем и считаем. Комплекс учебно-развивающих компьютерных игровых тренажеров по начальному обучению математике
Играем и считаем. Комплекс учебно-развивающих компьютерных игровых тренажеров по начальному обучению математике Параллельные прямые
Параллельные прямые Задача на арифметическую прогрессию (2)
Задача на арифметическую прогрессию (2)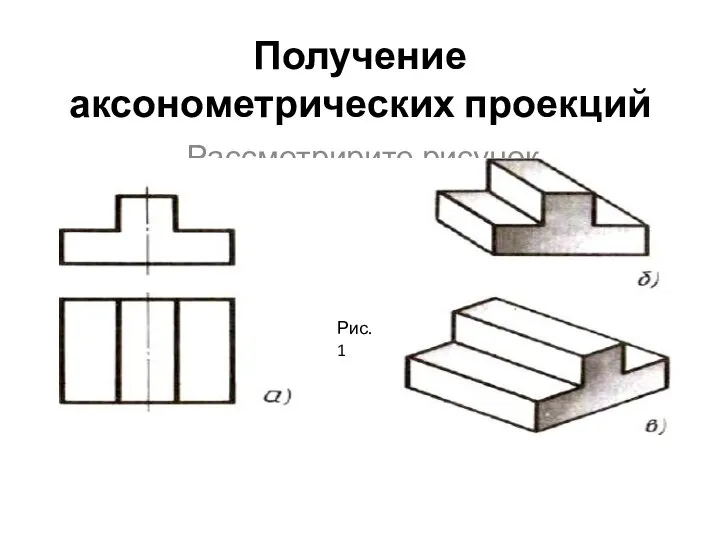 Получение аксонометрических проекций
Получение аксонометрических проекций Движение
Движение Виды кривых, замечательные кривые. Окружность и круг
Виды кривых, замечательные кривые. Окружность и круг