Содержание
- 2. Задача. Придать интерполяционной формуле более простой вид. Слагаемые должны располагаться в порядке убывания их значимости.
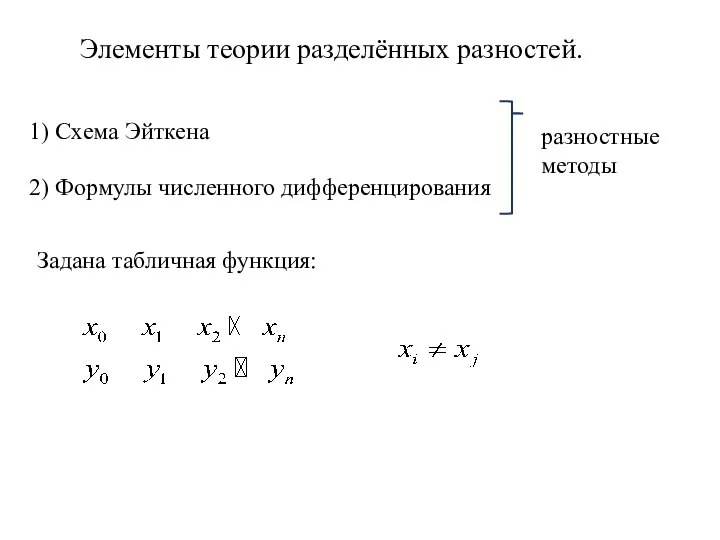
- 3. Элементы теории разделённых разностей. 1) Схема Эйткена 2) Формулы численного дифференцирования разностные методы Задана табличная функция:
- 4. разделённые разности первого порядка разделённые разности второго порядка
- 5. разделённая разность k-го порядка Полезные свойства разделённых разностей 1) Разделённая разность k-го порядка равна:
- 6. 2) Разделённая разность суммы или разности функций равна сумме или разности разделённых разностей слагаемых, соответственно уменьшаемого
- 7. Вывод: Разделённые разности n-го порядка многочлена n-й степени постоянны. (Все последующие равны нулю) Свойство 5 применяют
- 8. Построим таблицу разделённых разностей
- 9. Строим полином Ньютона Задана табличная функция: При построении полинома Ньютона в качестве базисных функций возьмем следующие:
- 10. График многочлена должен проходить через заданные узлы, т.е. Из этих условий найдём коэффициенты:
- 11. − разделённая разность 0-го порядка − разделённая разность 1-го порядка − разделённая разность 2-го порядка
- 12. Для равноотстоящих узлов: − разделённая разность 1-го порядка − разделённая разность 2-го порядка
- 13. Общая формула для коэффициента многочлена Ньютона имеет вид: Окончательный вид многочлена Ньютона: Этой формулой пользуются для
- 14. Второй интерполяционный многочлен Ньютона для интерполирования назад. 4) Разделённая разность есть симметрическая функция своих аргументов, т.е.
- 15. Погрешность многочлена Ньютона. где при
- 16. Пример. Вычислить в точках x = 0,1 и x = 4,5 значения функции, заданной таблично.
- 17. При воспользуемся первой формулой Ньютона. При воспользуемся второй формулой Ньютона.
- 19. Скачать презентацию















 Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром.
Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром. Построение сечений
Построение сечений Признаки равенства треугольников
Признаки равенства треугольников Решение систем линейных алгебраических уравнений. Тема 2
Решение систем линейных алгебраических уравнений. Тема 2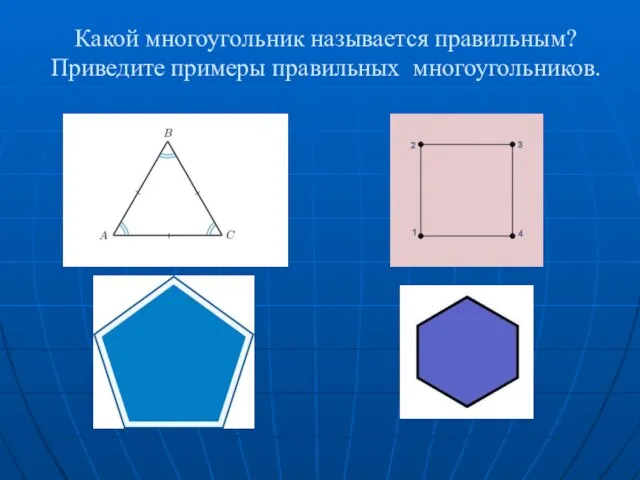 Какой многоугольник называется правильным? Приведите примеры правильных многоугольников
Какой многоугольник называется правильным? Приведите примеры правильных многоугольников Методы составления уравнений неголономной механики в задаче волнового твердотельного гироскопа
Методы составления уравнений неголономной механики в задаче волнового твердотельного гироскопа Построение сечений
Построение сечений Блок - схемы алгоритмов
Блок - схемы алгоритмов Графики
Графики Решение СЛУ
Решение СЛУ Сечение поверхностей плоскостью
Сечение поверхностей плоскостью Решение показательных уравнений. Корень уравнения
Решение показательных уравнений. Корень уравнения Пределы
Пределы Случаи сложения 470 +80 и вычитания 560-90
Случаи сложения 470 +80 и вычитания 560-90 Численные методы решения систем линейных уравнений
Численные методы решения систем линейных уравнений Комплексные корни квадратных уравнений
Комплексные корни квадратных уравнений Импорт-экспорт данных. Прикладные методы расчета и программные комплексы (5)
Импорт-экспорт данных. Прикладные методы расчета и программные комплексы (5) Геометричекие тела
Геометричекие тела Презентация на тему Математический калейдоскоп
Презентация на тему Математический калейдоскоп  Презентация на тему Умножение многочлена на многочлен
Презентация на тему Умножение многочлена на многочлен  Решение задач с пропорциональными величинами
Решение задач с пропорциональными величинами П 3
П 3 Логарифмические уравнения
Логарифмические уравнения Многогранники. Единица объема. Объем прямоугольного параллелепипеда
Многогранники. Единица объема. Объем прямоугольного параллелепипеда Функция нескольких переменных
Функция нескольких переменных Квадратичная функция
Квадратичная функция Квадратные неравенства
Квадратные неравенства Четырёхугольники. Тест
Четырёхугольники. Тест