Презентация на тему Простые числа

Цели и задачи работы:
Исследовать множество простых чисел.
Выяснить, существует ли математическая формула для их отыскания.
Выяснить, существует ли самое большое простое число?
Изучить сопутствующую теорию и историческое развитие данной темы.
Исследовать современное состояние изучаемого вопроса.

Содержание
Основная часть
1) Теоретические сведения
2) Решето Эратосфена
3) Таблица простых чисел до 1000
4) Работа с таблицей простых чисел
5) Теорема Евклида
6) Числа Мерсенна
7) Скатерть (спираль) Улама
8) Современные исследования
9) Количество простых чисел
Выводы
Список использованных источников

1) Теоретические сведения
Простое число — это натуральное число, которое имеет ровно 2 натуральных делителя (только 1 и самого себя).
Составное число — натуральное число большее 1, не являющееся простым.
1 – особое число, оно не является ни простым, ни составным
Таким образом, все натуральные числа, за исключением единицы, разбиваются на простые и составные. Изучением свойств простых чисел занимается теория чисел.
Простые числа-близнецы это пара простых чисел, отличающихся на 2.
Если натуральное число a делится на натуральное число b,то число b называют делителем числа a, а число а – кратным числа b.

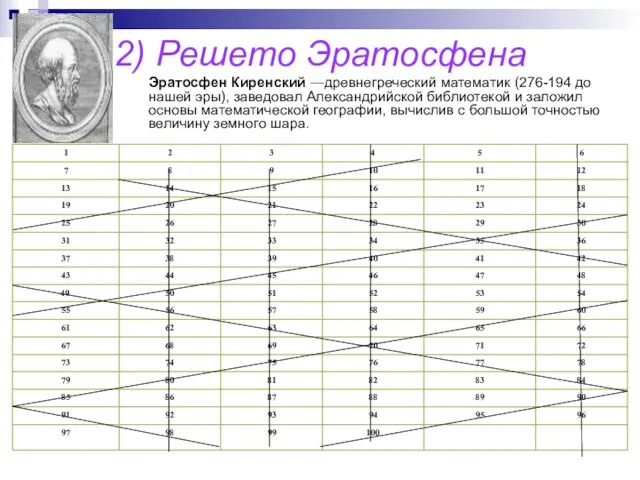
2) Решето Эратосфена
Эратосфен Киренский —древнегреческий математик (276-194 до нашей эры), заведовал Александрийской библиотекой и заложил основы математической географии, вычислив с большой точностью величину земного шара.

Итак, «Решето Эратосфена»
работает как своего рода аналоговая вычислительная машина. И, значит, вот что изобрел великий грек: он изобрел СЧЕТНУЮ МАШИНУ. Простые числа располагаются на числовом ряду весьма причудливым образом, но, создав Решето Эратосфена достаточно большого размера, мы отсеем (построим) их ВСЕ без исключения. Все они окажутся в дырках совершенно правильного геометрически Решета!
Найти редкие оазисы простых чисел, затерянные в обширных пустынях составных чисел, нелегко. Решето Эратосфена позволяет это сделать!
Анализируя «Решето Эратосфена» видно, что все простые числа либо на 1 меньше, либо на 1 больше чисел, кратных 6.

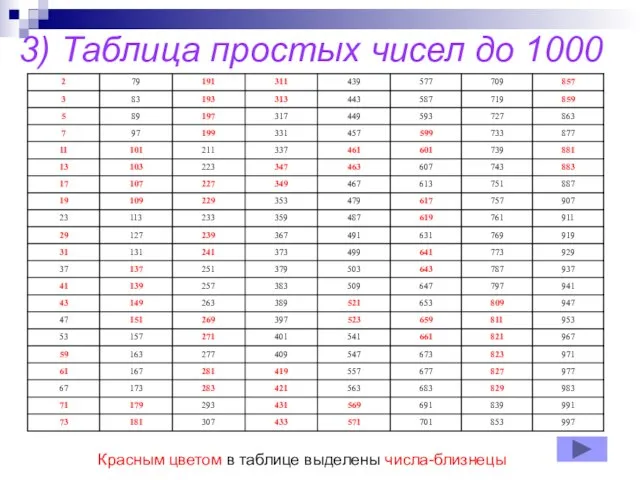
3) Таблица простых чисел до 1000
Красным цветом в таблице выделены числа-близнецы

4) Работа с таблицей простых чисел
Количество простых чисел до 1000: 168 чисел.
Простые числа от 2 до 100: 25 чисел
Простые числа от 100 до 200: 21 число
Простые числа от 200 до 300: 16 чисел
Простые числа от 300 до 400: 16 чисел
Простые числа от 400 до 500: 17 чисел
Простые числа от 500 до 600: 14 чисел
Простые числа от 600 до 700: 16 чисел
Простые числа от 700 до 800: 14 чисел
Простые числа от 800 до 900: 15 чисел
Простые числа от 900 до 1000: 14 чисел
Числа - близнецы до 500: 24 пары
Числа - близнецы от 500 до 1000: 11 пар
Всего до тысячи 35 пар чисел-близнецов.
Вывод: количество простых чисел постепенно уменьшается.

5) Теорема Евклида
Евклид - древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Биография, сведения о нем крайне скудны. Его научная деятельность протекала в Александрии в 3 веке до н. э.
Евклид — первый математик александрийской школы.
Теорема.
Евклид доказал, что простых чисел бесконечно много. Можно сказать также, что среди простых чисел нет самого большого числа.
Так две с лишним тысячи лет назад Евклид лишил математиков надежды получить когда-нибудь полный список простых чисел.
Много ученых пытались найти общую формулу для записи простых чисел, но все их попытки не увенчались успехом.

6) Числа Мерсенна
Маре́н Мерсе́нн (1588 — 1648) — французский математик, физик, философ и теолог. На протяжении первой половины XVII века был по существу координатором научной жизни Европы, ведя активную переписку практически со всеми видными учёными того времени.
Числа вида 2 р -1, где р – простое число, называются числами Мерсенна, впервые заметившего, что среди таких чисел много простых.
Это числа: 3, 7, 31, 127, 2047, 8191, 131071, 524287 при р = 2, 3, 5, 7, 11, 13, 17, 19. Среди них есть простые: 3, 7, 31, 127. Однако, среди них есть и составные.
Например, при р = 11, это число 2047 = 23∙89 – составное.

7) Скатерть (спираль) С. Улама
Станислав Мартин Улам (13 апреля, 1909, Львов —13 мая, 1984, Санта-Фе) — выдающийся польский математик, ученик Банаха, переехавший в Принстон в 1934 году и позднее участвовавший в создании американской водородной бомбы в рамках ядерного проекта Лос-Аламосской лаборатории, что в городе Лос-Аламосе, также внёс большой вклад в развитие некоторых математических методов.
Метод «Скатерти Станислава Улама» (1963 г.) относится не к традиционной математике, а к числонавтике. Суть и цель его метода заключается в выявлении и визуализации простых чисел из натуральных. Это великолепная находка математика, который, в отличие от обычных людей, прекрасно ЧУВСТВОВАЛ цифры и числа. Именно это и позволило ему уловить неожиданный геометрический феномен простых чисел.
Сам метод появился из неких числовых манипуляций, которые С. Улам случайно осуществил на бумажной столовой салфетке....
Он начертил на ней вертикальные и горизонтальные линии и хотел заняться составлением шахматных этюдов, но потом передумал и начал нумеровать пересечения, поставив в центре 1, и, двигаясь по спирали против часовой стрелки, записывал все натуральные числа до 100. Без всякой задней мысли Улам обводил все простые числа кружками. Каково было его удивление, когда он увидел, что простые числа стали выстраиваться вдоль прямых линий!

На рисунке простые числа отмечены зеленым цветом.
Видно, как простые числа располагаются на прямых диагональных линиях.
В вычислительном отделе Лос-Аламосской лаборатории, где работал Улам, имелась магнитная лента, на которой было записано 90 млн. простых чисел. Улам вместе с Майроном Л. Стейном и Марком Б. Уэллсом составили программу для вычислительной машины МАNIAK, позволившую нанести на спираль последовательные целые числа от 1 до 65000.

8) Современные исследования
Тайн у природы ещё предостаточно. Реальность имеет множество форм своего проявления и отображения. Но, рано или поздно, люди всегда пытаются проникнуть в скрытые тайны, чтобы постигнуть их.
Современным исследователем данного вопроса является Алексей Алексеевич Корнеев, который метод Улама назвал «Методом числового вмещения» (А.А.Корнеев, Москва, 2007-2008г.).
Кроме этого, он утверждает, что при анализе этого метода не было сделано должных выводов и обобщений в отношении смысла этого феномена. Например, можно было сразу же задуматься о фундаментальной роли и значении спиральной формы движения.

Мы видим тип этого движения буквально повсюду
Это и строение галактик во Вселенной, это и формы живого (спиральные тела ракушек, улиток, и пр.), это, наконец, строение наследственного вещества живых существ – молекул ДНК.

Глобальный Принцип Улама & Ko (гипотеза)
Поскольку в наблюдаемом нами мире преобладают спиральные формы движения (как и в опыте С. Улама), то для тех же галактик вполне разумно допустить существование неких незримых, но вполне определённых траекторий, вдоль которых просто обязаны локализоваться особые точки пространства (или особые объекты), по аналогии с точками локализации простых чисел.
Корнеев утверждает, что это было бы закономерным явлением, ибо в строении и в структуре галактик мы наблюдаем само естество Природы. Здесь действуют именно натуральные процессы и ряды явлений, прообразами для которых вполне могут быть натуральные и простые числа…

Эта гипотеза графически отображена на рисунке

Таким образом,
Корнеев предлагает провести практические исследования в сфере астрономии для обнаружения особых геометрических феноменов и особых объектов, подобных расположению простых чисел на скатерти С. Улама.
Он предсказывает, что, если изложенный им взгляд на данную проблему будет воспринят учеными других специальностей, то не только астрономы, но и биологи, а также генетики порадуют нас своими неожиданными открытиями из жизни ... «спиральных реальностей»!
Кроме этого, Корнеев утверждает, что и сами числа изучены недостаточно, у них есть скрытые качества! Не зря ряд чисел удивительным образом встраивается во все природные явления

Итак, в наше время изучение простых чисел продолжается…
Современные компьютеры помогают находить большие простые числа, но их возможности тоже ограничены, так как множество простых чисел бесконечно.
С помощью ЭВМ найдено самое большое простое число Мерсенна
2 р -1 при р = 216091.
Самые большие известные числа-близнецы
1 000 000 009 649 и 1 000 000 009 651.
Нет пока ответа на вопрос о том, существует ли самая большая пара чисел-близнецов.

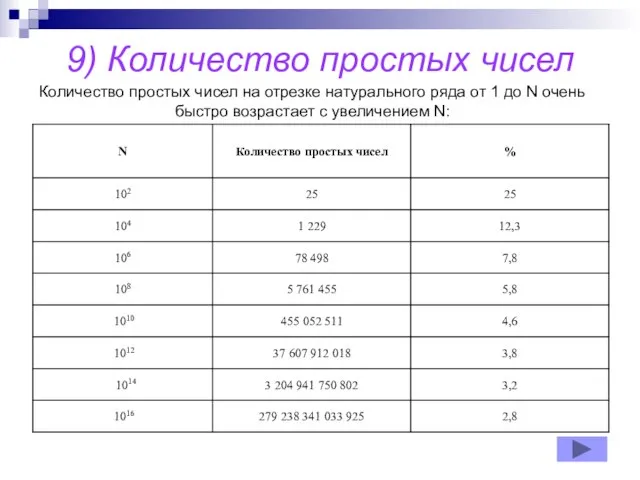
9) Количество простых чисел
Количество простых чисел на отрезке натурального ряда от 1 до N очень быстро возрастает с увеличением N:

3. Выводы
Изучив весь материал, я пришла к выводу, что решением задачи о Млечном пути является: СПИРАЛЬ!
Можно сказать, что простые числа представляют собой как бы кирпичики, из которых строятся все остальные числа.
Для простых чисел не существует формулы, по которой их можно вычислить.
Не существует самого большого простого числа, последовательность простых чисел бесконечна.
Многие ученые на протяжении многих веков вносили свой вклад в изучение темы «Простые числа»
В настоящее время исследование темы продолжается, ученые делают, и будут делать новые открытия!