Объём произвольного тела вращения

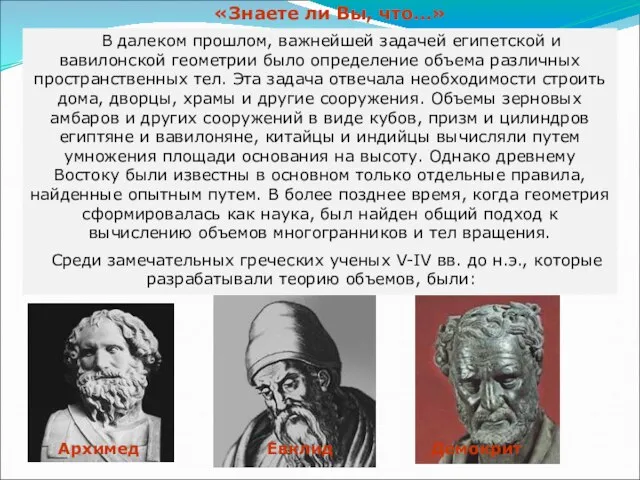
В далеком прошлом, важнейшей задачей египетской и вавилонской геометрии было определение объема различных пространственных тел. Эта задача отвечала необходимости строить дома, дворцы, храмы и другие сооружения. Объемы зерновых амбаров и других сооружений в виде кубов, призм и цилиндров египтяне и вавилоняне, китайцы и индийцы вычисляли путем умножения площади основания на высоту. Однако древнему Востоку были известны в основном только отдельные правила, найденные опытным путем. В более позднее время, когда геометрия сформировалась как наука, был найден общий подход к вычислению объемов многогранников и тел вращения.
Среди замечательных греческих ученых V-IV вв. до н.э., которые
разрабатывали теорию объемов, были:
«Знаете ли Вы, что…»
Архимед
Евклид
Демокрит

Геометрические тела в архитектурных сооружениях

Геометрические тела в архитектурных сооружениях

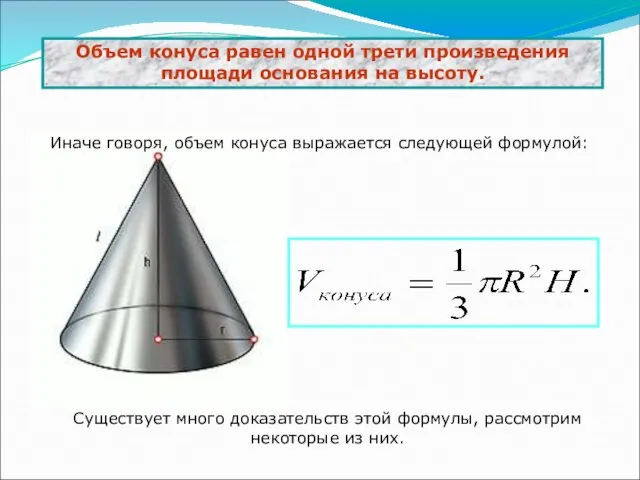
Объем конуса равен одной трети произведения площади основания на высоту.
Иначе говоря, объем конуса выражается следующей формулой:
Существует много доказательств этой формулы, рассмотрим некоторые из них.

Первое доказательство.
За величину объёма конуса принимается предел, к которому стремится объем правильной пирамиды, вписанной в конус, при неограниченном удвоении числа сторон её основания.

Определение объема произвольного тела вращения
Интегральное исчисление, созданное Ньютоном и Лейбницем, превратило вычисление объемов в стандартную операцию. Она записывается следующей формулой:
Определение объема произвольного тела вращения

Второе доказательство:
Сечение конуса плоскостью, параллельной основанию, подобно основанию. Если плоскость проходит на расстоянии х от вершины, то коэффициент подобия равен
Поэтому площадь сечения Q(x) такой плоскостью равна:
где S - площадь основания.
Значит, объем конуса К будет:
x
H
Sосн
Sсеч

Третье доказательство:
0
x
y
H
y=kx
α
α
R
У=kx

От теории - к практике…
Задача 1.
Куча песка имеет форму конуса, длина окружности основания которого 31,4 м, а образующая 5,4 м. Сколько трехтонных машин потребуется для вывоза песка, если масса 1м3 песка составляет 2т?
Задача 2.
Вибросито для процеживания окрасочных составов имеет форму конуса. Боковая поверхность его вдвое больше площади основания. Определите вместимость вибросита, если радиус основания R = 20 см.

«… Читал я где-то,
Что царь однажды воинам своим
Велел снести земли по горсти в кучу.
И гордый холм возвысился,
И царь мог с высоты с весельем озирать
И дол, покрытый белыми шатрами,
И море, где бежали корабли.»
В своем драматическом произведении «Скупой рыцарь» Александр Сергеевич Пушкин рассказывает одну старинную легенду восточных народов:

СПРАВКА
1горсть ≈ 0,2 дм3
Войско в 100 000 воинов считалось очень внушительным.
Угол откоса ≤ 450, иначе земля начнет осыпаться.
Используя полученные знания, проверьте, прав ли Александр Сергеевич Пушкин?

Решение к задаче 4*. V=0,2. 100 000=20 000(дм3)=20(м3).
Так как H=R, то V=1/3πH3 , Н3=3*Y/π
Ответ: 2,7 метров.
Надо обладать очень богатым воображением,
чтобы земляную кучу в 2,7 м
(1,5 человеческого роста)
назвать «гордым холмом».
Сделав расчет для меньшего угла, мы получили бы
еще более скромный
результат

ИСТОРИЧЕСКАЯ СПРАВКА
У Аттилы было самое многочисленное войско, которое знал древний мир.
Историки оценивают его в 700 000 человек.
Если бы даже все воины Аттилы участвовали
в насыпании холма, образовалась бы куча повыше вычисленной нами,
но не очень.
Домашнее задание
Попробуйте сами дома вычислить высоту такого кургана и подумать, удовлетворила ли бы такая высота честолюбие Аттилы или нет?

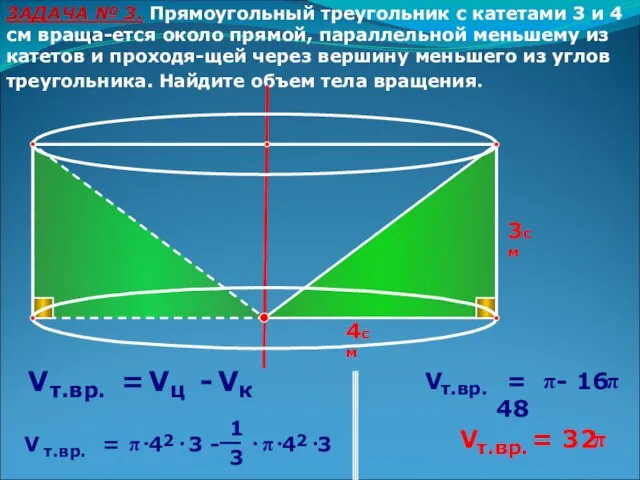
ЗАДАЧА № 3. Прямоугольный треугольник с катетами 3 и 4 см враща-ется около прямой, параллельной меньшему из катетов и проходя-щей через вершину меньшего из углов треугольника. Найдите объем тела вращения.
4см
3см