Содержание
- 2. Находим приращение функции Δy=f(x+Δx)-f(x) 2 3 Составляем отношение: 4 Находим
- 3. ПРИМЕР. Найдем производную функции Дадим аргументу х приращение Δх и найдем значение функции y+Δy: 1 2
- 4. 3 Составляем отношение
- 5. Находим 4 Полученный результат является частным случаем производной от степенной функции Можно показать, что в общем
- 6. производная степенной функции
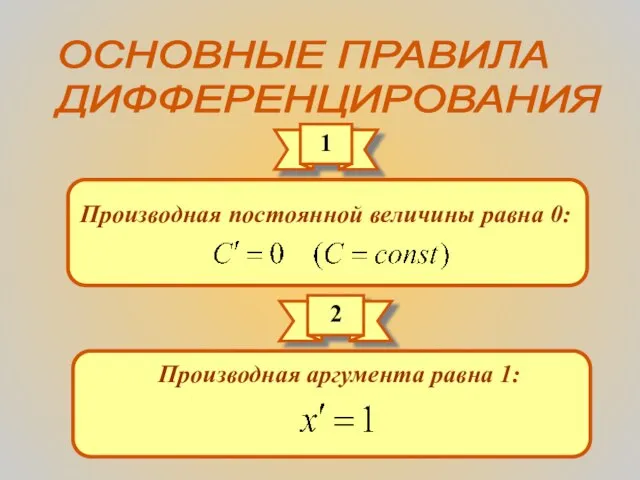
- 7. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ 1 Производная постоянной величины равна 0: 2 Производная аргумента равна 1:
- 8. 3 Производная алгебраической суммы (разности) конечного числа дифференцируемых функций равна сумме (разности) производных этих функций:
- 9. ДОКАЗАТЕЛЬСТВО: Пусть u=u(x) и v=v(x) -дифференцируемые функции. Найдем производную функции y=u + v. Дадим аргументу х
- 10. Находим приращение функции Составляем отношение Находим предел этого отношения:
- 11. 4 Производная произведения двух дифференцируемых функций равна сумме произведений производной первого сомножителя на второй и производной
- 12. ДОКАЗАТЕЛЬСТВО: Пусть u=u(x) и v=v(x) -дифференцируемые функции. Найдем производную функции y=uv. Дадим аргументу х приращение Δх,
- 13. Находим приращение функции Составляем отношение
- 14. Находим предел этого отношения: Имеем по определению производной:
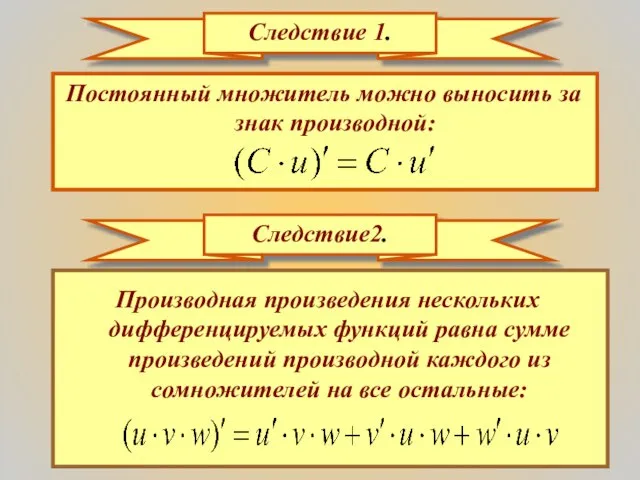
- 15. Следствие 1. Постоянный множитель можно выносить за знак производной: Следствие2. Производная произведения нескольких дифференцируемых функций равна
- 16. 5 Производная частного двух дифференцируемых функций находится по формуле:
- 17. ПРИМЕРЫ. 1 Найти производную функции и вычислить ее значение в точке х=1.
- 18. Решение. Находим значение производной в точке х=1:
- 19. 2 Найти производную функции и вычислить ее значение в точке х=1.
- 20. Решение. Находим значение производной в точке х=1:
- 21. 3 Найти производную функции и вычислить ее значение в точке х=1.
- 23. Скачать презентацию


















 Презентация на тему Параллельность прямых и плоскостей (10 класс)
Презентация на тему Параллельность прямых и плоскостей (10 класс)  Презентация на тему Эллипс
Презентация на тему Эллипс  Решение примеров
Решение примеров Приёмы устных вычислений
Приёмы устных вычислений Алгебра. Лекция 3
Алгебра. Лекция 3 Сложение десятичных дробей
Сложение десятичных дробей Презентация на тему ЗАДАНИЯ С РАЗВЕРНУТЫМ ОТВЕТОМ ПОВЫШЕННОГО УРОВНЯ СЛОЖНОСТИ С5. ПОДГОТОВКА К ЕГЭ
Презентация на тему ЗАДАНИЯ С РАЗВЕРНУТЫМ ОТВЕТОМ ПОВЫШЕННОГО УРОВНЯ СЛОЖНОСТИ С5. ПОДГОТОВКА К ЕГЭ  Прямоугольник. Ось симметрии
Прямоугольник. Ось симметрии Прямоугольная система координат в пространстве. Координаты середины отрезка. Расстояние между двумя точками. Уравнение сферы
Прямоугольная система координат в пространстве. Координаты середины отрезка. Расстояние между двумя точками. Уравнение сферы Сочетание традиций и инноваций в учебниках математики Н. Я. Виленкина – залог успешного обучения
Сочетание традиций и инноваций в учебниках математики Н. Я. Виленкина – залог успешного обучения Творческая работа по математике (Г.В. Дорофеев; Т.Н. Миракова; Т.Б. Бука 2-3 класс)
Творческая работа по математике (Г.В. Дорофеев; Т.Н. Миракова; Т.Б. Бука 2-3 класс)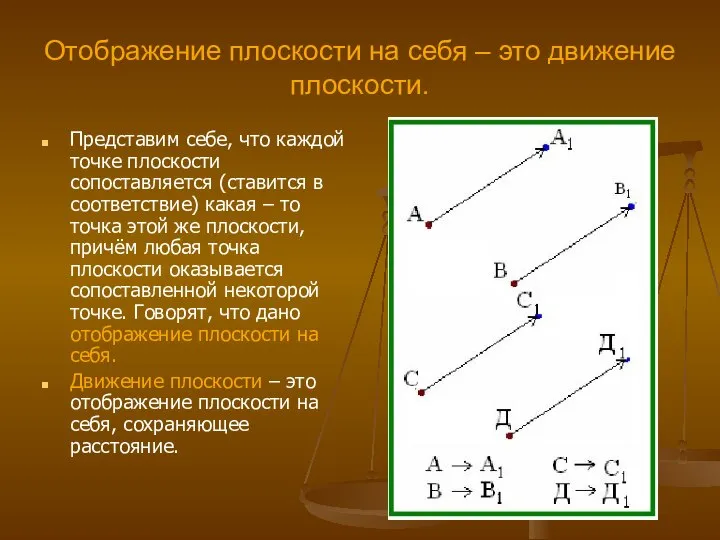 Геометрические преобразования плоскости
Геометрические преобразования плоскости Теория вероятностей. Подготовка к ГИА
Теория вероятностей. Подготовка к ГИА Точки перегиба
Точки перегиба Путешествие в Изумрудный город
Путешествие в Изумрудный город Многоликая теорема Пифагора
Многоликая теорема Пифагора Декартова система координат
Декартова система координат Можно ли измерить длину окружности?
Можно ли измерить длину окружности? Динамика нелинейного тентообразного отображения с параметром
Динамика нелинейного тентообразного отображения с параметром Квадратный трехчлен. Самостоятельная работа
Квадратный трехчлен. Самостоятельная работа Элементы аналитической геометрии. Уравнение прямой на плоскости
Элементы аналитической геометрии. Уравнение прямой на плоскости Математический дизайн
Математический дизайн Устная работа. Вычисления
Устная работа. Вычисления Окружность. Основные теоремы
Окружность. Основные теоремы Соответствия между множествами. Отображения. Функции
Соответствия между множествами. Отображения. Функции Задача о смесях
Задача о смесях Схема Бернулли. Формула полной вероятности. Формула Байеса
Схема Бернулли. Формула полной вероятности. Формула Байеса Признаки делимости на 11
Признаки делимости на 11