Содержание
- 2. Системой m линейных уравнений с n неизвестными х1, х2, …, хn называется система вида aij -
- 3. Решением системы (*) называется такой набор чисел (с1, с2,…, сn), что при его подстановке в систему
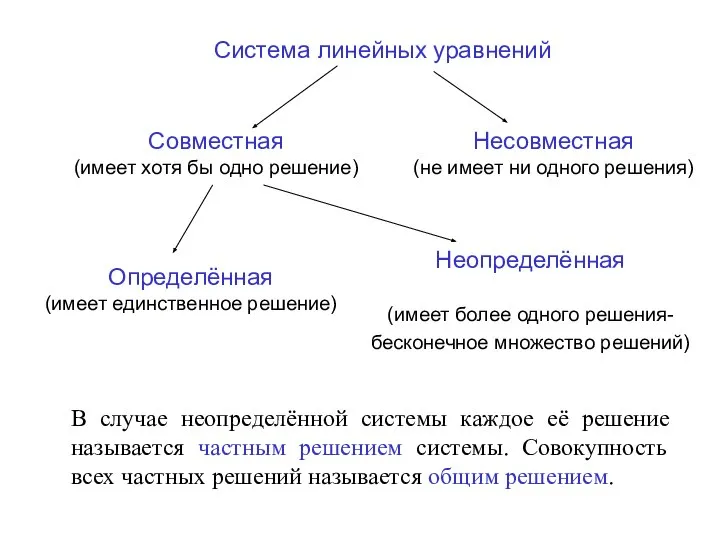
- 4. Система линейных уравнений Совместная (имеет хотя бы одно решение) Несовместная (не имеет ни одного решения) Определённая
- 5. Если b1=b2=…=bm=0, то система называется однородной; в противном случае она называется неоднородной. Две системы называются эквивалентными
- 6. Элементарными преобразованиями линейной системы называются следующие преобразования: - перестановка уравнений системы; - умножение или деление коэффициентов
- 7. Систему (*) можно записать в матричной форме: АХ=В, где матрица коэффициентов системы; матрица-столбец (вектор-столбец) неизвестных матрица-столбец
- 8. Расширенной матрицей системы (*) называется матрица А В
- 9. Исследование системы линейных уравнений. Теорема Кронекера-Капелли. Система линейных уравнений (*) совместна тогда и только тогда, когда
- 10. Исследовать систему линейных уравнений означает определить, совместна она или нет, а для совместной системы- выяснить, является
- 11. Правила решения произвольной системы линейных уравнений. Найти ранги основной и расширенной матриц системы. Если rang(A)≠rang(A|B), то
- 12. Выразить базисные (главные) неизвестные через свободные. Придавая свободным неизвестным произвольные значения, получим соответствующие значения базисных (главных)
- 13. 3. Метод Гаусса Систему уравнений приводят к эквивалентной ей системе с треугольной матрицей (к ступенчатому виду).
- 14. 1. Исследовать систему линейных уравнений. Если она совместна, то найти её общее и одно частное решение.
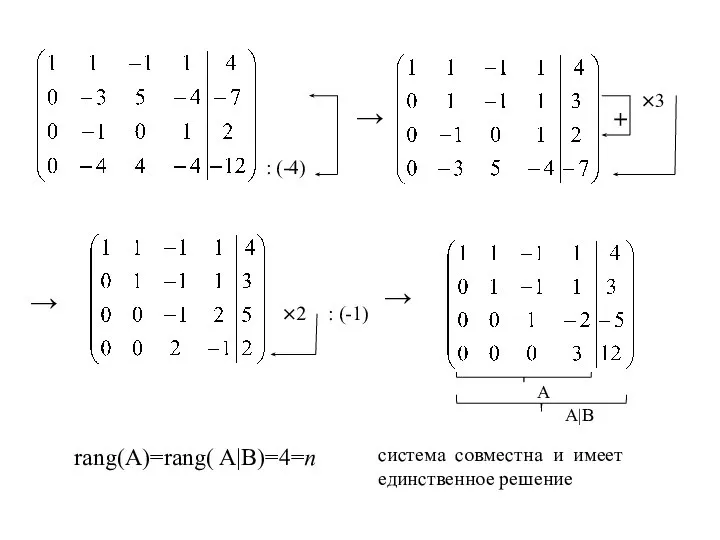
- 15. Прямой ход ×(-2) ×(-1) ×(-3) →
- 16. → : (-4) + ×3 → ×2 : (-1) → rang(A)=rang( A|B)=4=n система совместна и имеет
- 17. обратный ход Ответ: (1; 2; 3; 4)
- 18. 2. Исследовать систему линейных уравнений. Если она совместна, то найти её общее и одно частное решение.
- 19. ×(-6) ×7 ×3 →
- 20. → + → rang(A)=rang(A|B)=2 система совместна и имеет бесконечное множество решений базисный минор порядка r =2:
- 22. общее решение х1 х2
- 23. пусть тогда частное решение Ответ: общее решение: частное решение: Делаем проверку и записываем ответ:
- 24. 3. Исследовать систему линейных уравнений. Если она совместна, то найти её общее и одно частное решение.
- 25. → rang(A)≠rang(A|B) ⇒ система несовместна rang(A)=2; rang(A|B)=3 А A|B Ответ: система несовместна
- 26. Если b1=b2=…=bm=0, то система называется однородной.
- 27. Однородная система линейных уравнений. Пусть дана система m линейных однородных уравнений с n неизвестными х1, х2,
- 28. Однородная система всегда совместна, так как существует тривиальное решение х1= х2=…=хn=0 Однородная система имеет бесконечное множество
- 29. 1. Решить систему линейных уравнений :
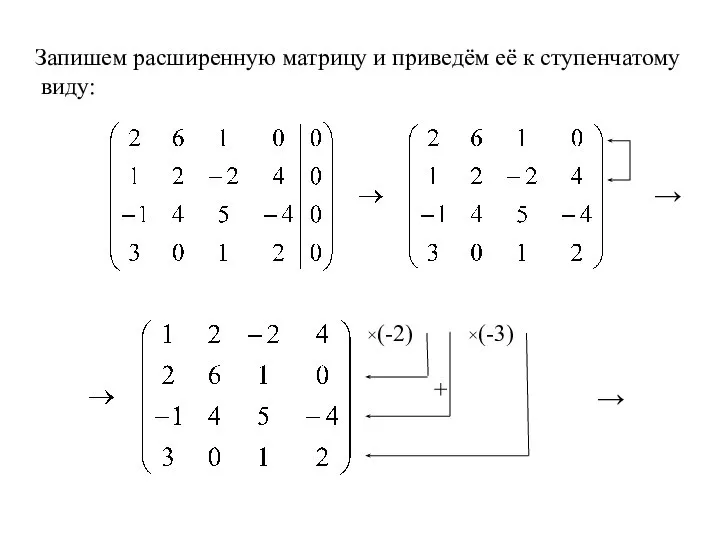
- 30. Запишем расширенную матрицу и приведём её к ступенчатому виду: ×(-2) ×(-3) → → +
- 31. ×(-3) ×3 → : 2 : 12 ×11
- 32. rang(A)=rang(A|B)=4=(n=4) ⇒ система совместна и определённа, то есть имеет единственное решение х1= х2= х3 =х4=0. А
- 33. Ответ: (0, 0, 0, 0)
- 34. 2. Решить систему линейных уравнений : ×(-2) : 3 →
- 35. rang(A)=rang(A|B)=2 система совместна и имеет бесконечное множество решений базисный минор порядка r =2: базисные переменные: х1,
- 36. ⇒ Тогда общее решение системы: (0, х3, х3)
- 38. Скачать презентацию















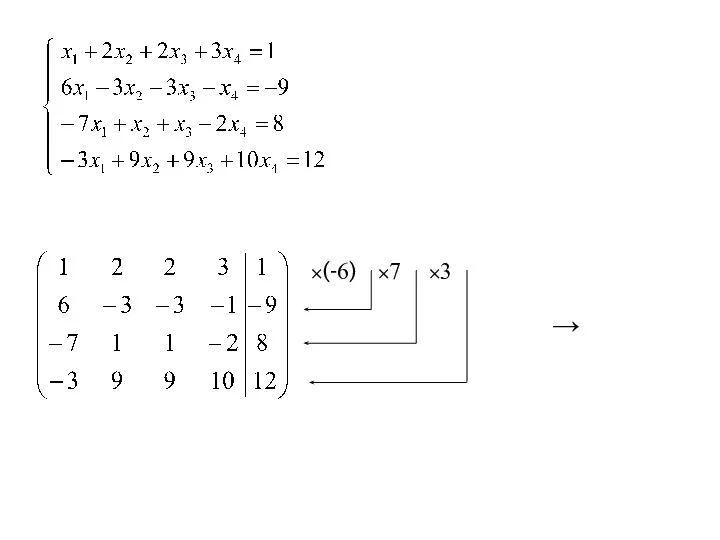

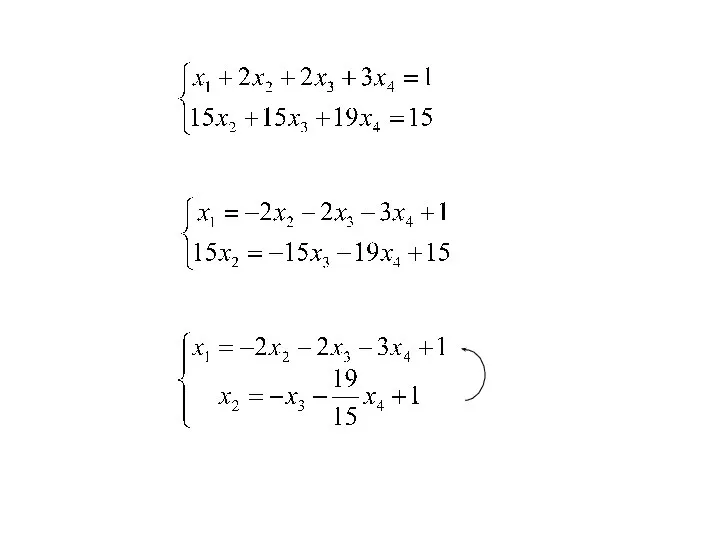
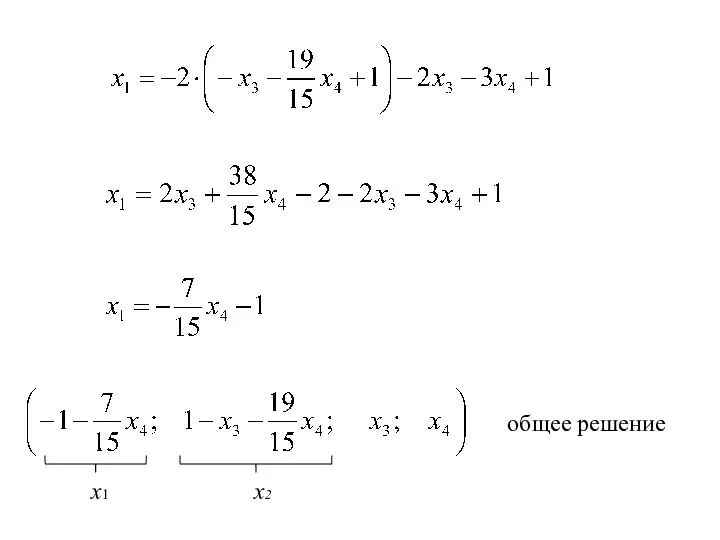







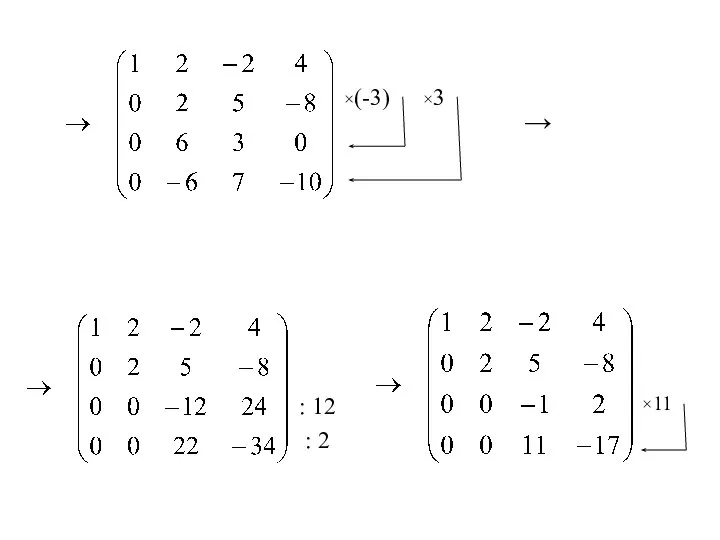





 Основы математической статистики
Основы математической статистики Какой многоугольник называется правильным? Приведите примеры правильных многоугольников
Какой многоугольник называется правильным? Приведите примеры правильных многоугольников Презентация на тему Комбинаторные задачи
Презентация на тему Комбинаторные задачи  Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента Методика изучения Массы
Методика изучения Массы Линейная функция
Линейная функция Параллельность прямых и плоскостей в пространстве с решением
Параллельность прямых и плоскостей в пространстве с решением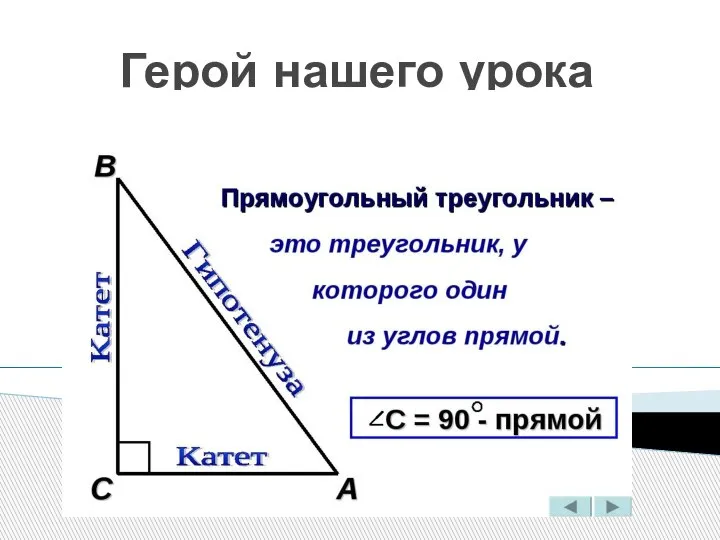 Площадь прямоугольного треугольника
Площадь прямоугольного треугольника Счет
Счет Геометрические приложения двойных интегралов
Геометрические приложения двойных интегралов Устный счёт. Транспорт
Устный счёт. Транспорт Подготовка к ЕГЭ В8
Подготовка к ЕГЭ В8 Площадь треугольника
Площадь треугольника Как вычислить площадь поверхности тела человека
Как вычислить площадь поверхности тела человека Решение задач с помощью пропорций
Решение задач с помощью пропорций Треугольники. Треугольник в науке
Треугольники. Треугольник в науке Клуб весёлых и находчивых. Турнир любителей математики
Клуб весёлых и находчивых. Турнир любителей математики Цилиндр
Цилиндр Применение параллелограмма
Применение параллелограмма Медиана, биссектриса, высота
Медиана, биссектриса, высота Презентация на тему Понятие движения (9 класс)
Презентация на тему Понятие движения (9 класс)  Коэффициенты квадратного уравнения
Коэффициенты квадратного уравнения Логические и традиционные головоломки
Логические и традиционные головоломки 6. СЛАУ. Методы решения (1)
6. СЛАУ. Методы решения (1) Треугольники. Основные определения
Треугольники. Основные определения 6a04a5dd-75c3-461b-a240-737df2a5d137
6a04a5dd-75c3-461b-a240-737df2a5d137 Отношения и пропорция
Отношения и пропорция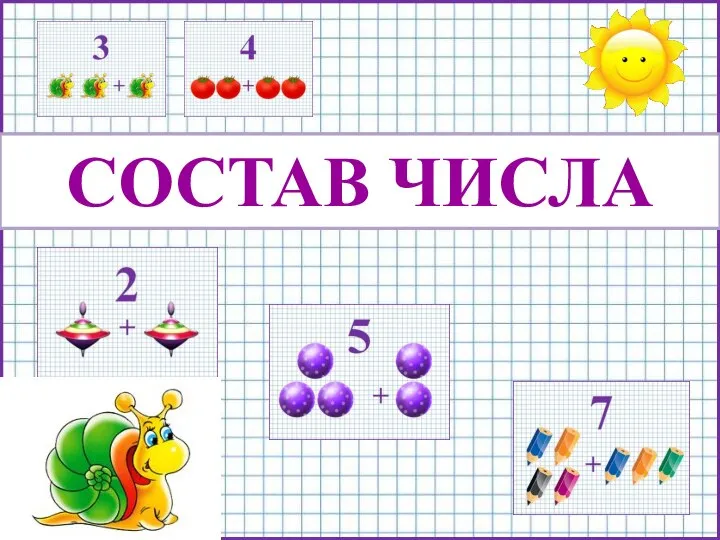 Состав чисел первого десятка
Состав чисел первого десятка