Презентация на тему Сечения призмы

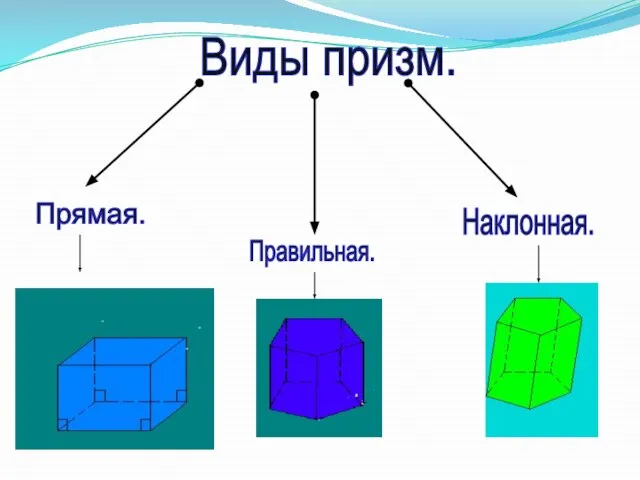
Виды призм.
Прямая.
Правильная.
Наклонная.

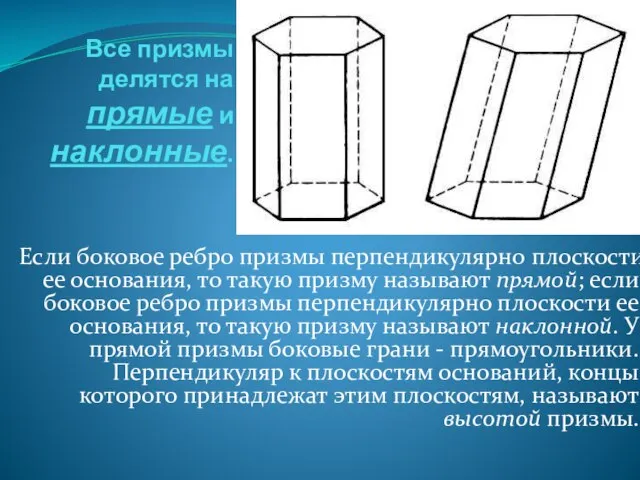
Все призмы делятся на прямые и наклонные.
Если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют прямой; если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют наклонной. У прямой призмы боковые грани - прямоугольники. Перпендикуляр к плоскостям оснований, концы которого принадлежат этим плоскостям, называют высотой призмы.

Свойства призмы.
1. Основания призмы являются равными многоугольниками.
2. Боковые грани призмы являются параллелограммами.
3о. Боковые ребра призмы равны.

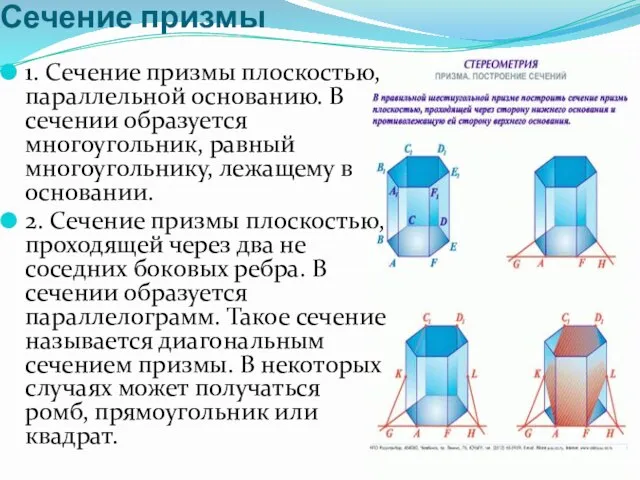
Сечение призмы
1. Сечение призмы плоскостью, параллельной основанию. В сечении образуется многоугольник, равный многоугольнику, лежащему в основании.
2. Сечение призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется параллелограмм. Такое сечение называется диагональным сечением призмы. В некоторых случаях может получаться ромб, прямоугольник или квадрат.

Наиболее доступными и эффективными методами построения сечения призмы являются три метода:
1. Метод следов.
3. Комбинированный метод.
2. Метод вспомогательных сечений.
www.matematika-na5.narod.ru

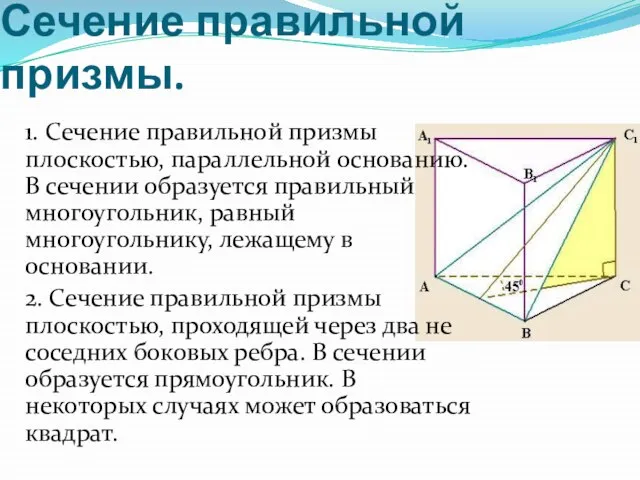
Сечение правильной призмы.
1. Сечение правильной призмы плоскостью, параллельной основанию. В сечении образуется правильный многоугольник, равный многоугольнику, лежащему в основании.
2. Сечение правильной призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется прямоугольник. В некоторых случаях может образоваться квадрат.

Задача.
Дано: Сторона основания правильной треугольной призмы равна 8 см, боковое ребро - 6 см. Найдите Sсеч, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.
Решение: Треугольник A1B1C1 - равнобедренный(A1B=C1B как диагональ равных граней)
1)Рассмотрим треугольник BCC1– прямоугольный
BC12=BС2+CC12
BC1= √ 64+36=10 см
2) Рассмотрим треугольник BMC1– прямоугольный
BC12=BM2+MC12
BM2=BC12-MC12
BM2=100-16=84
BM= √ 84=2 √ 21 см
3) Sсеч=12 A1C1*BM= 12*2√ 21 см*8=8 √ 21

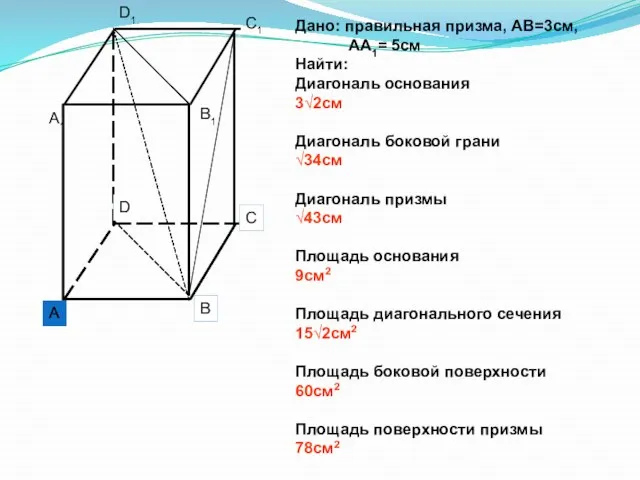
Дано: правильная призма, АВ=3см,
АА1= 5см
Найти:
Диагональ основания
3√2см
Диагональ боковой грани
√34см
Диагональ призмы
√43см
Площадь основания
9см2
Площадь диагонального сечения
15√2см2
Площадь боковой поверхности
60см2
Площадь поверхности призмы
78см2

Применение призмы в архитектуре