Презентация на тему Симметрия 8 класс

ЗАДАЧА №1
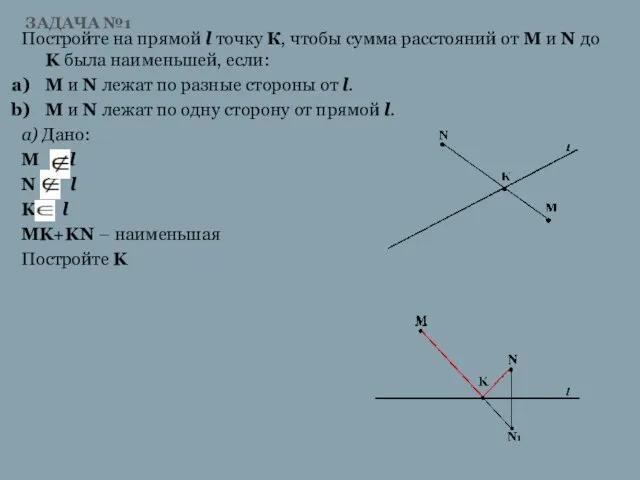
Постройте на прямой l точку К, чтобы сумма расстояний от M и N до K была наименьшей, если:
M и N лежат по разные стороны от l.
M и N лежат по одну сторону от прямой l.
а) Дано:
М l
N l
K l
MK+KN – наименьшая
Постройте K

ЗАДАЧА №2
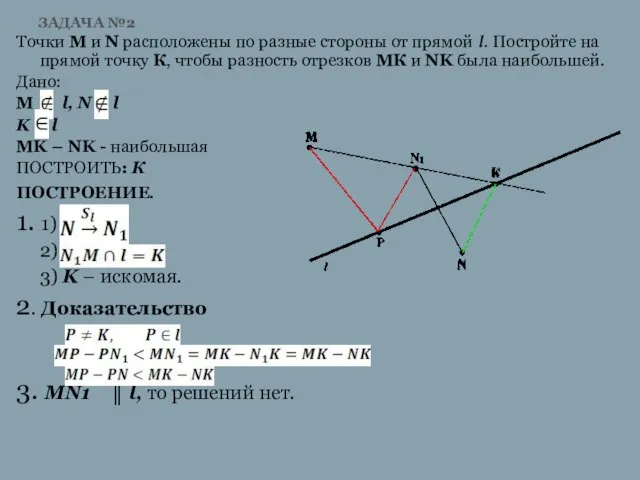
Точки M и N расположены по разные стороны от прямой l. Постройте на прямой точку К, чтобы разность отрезков МК и NK была наибольшей.
Дано:
M l, N l
K l
MK – NK - наибольшая
ПОСТРОИТЬ: К
ПОСТРОЕНИЕ.
1. 1)
2)
3) K – искомая.
2. Доказательство
3. МN1 ║ l, то решений нет.

ЗАДАЧА №3
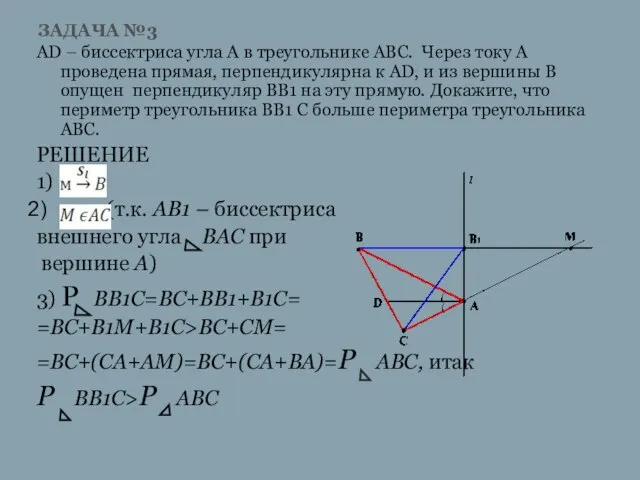
AD – биссектриса угла А в треугольнике АВС. Через току А проведена прямая, перпендикулярна к АD, и из вершины В опущен перпендикуляр ВВ1 на эту прямую. Докажите, что периметр треугольника ВВ1 С больше периметра треугольника АВС.
РЕШЕНИЕ
1)
(т.к. АВ1 – биссектриса
внешнего угла ВАС при
вершине А)
3) Р ВВ1С=ВС+ВВ1+В1С=
=ВС+В1М+В1С>ВС+СМ=
=ВС+(СA+AM)=BC+(CA+BA)=P ABC, итак
P BB1C>Р АВС

ЗАДАЧА №4
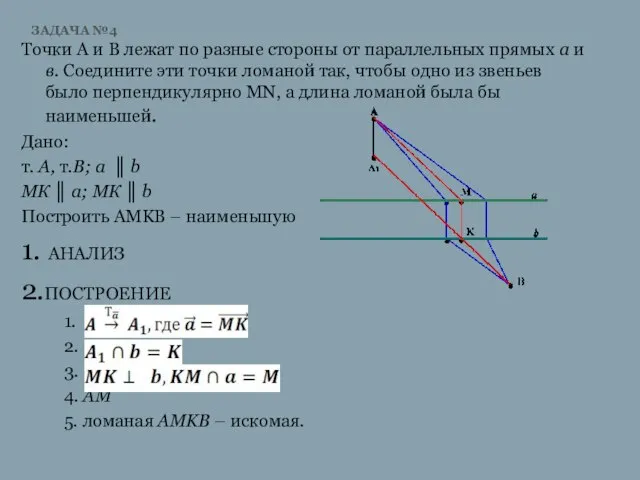
Точки А и В лежат по разные стороны от параллельных прямых а и в. Соедините эти точки ломаной так, чтобы одно из звеньев было перпендикулярно МN, а длина ломаной была бы наименьшей.
Дано:
т. А, т.B; а ║ b
МК ║ a; MК ║ b
Построить AMKВ – наименьшую
1. АНАЛИЗ
2.ПОСТРОЕНИЕ
1.
2.
3.
4. AM
5. ломаная AMKB – искомая.

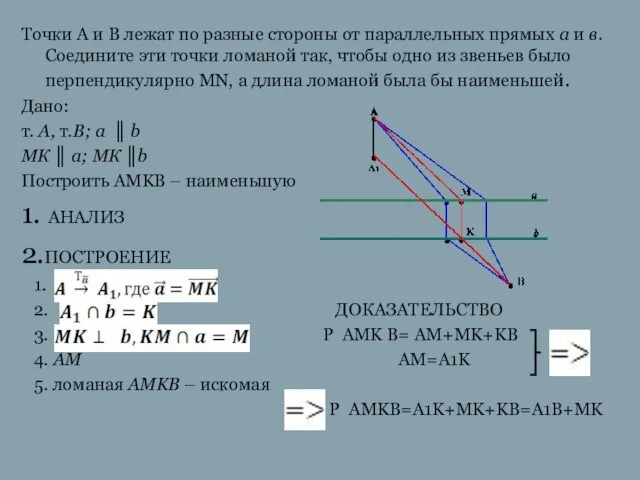
Точки А и В лежат по разные стороны от параллельных прямых а и в. Соедините эти точки ломаной так, чтобы одно из звеньев было перпендикулярно МN, а длина ломаной была бы наименьшей.
Дано:
т. А, т.B; а ║ b
МК ║ a; MК ║b
Построить AMKВ – наименьшую
1. АНАЛИЗ
2.ПОСТРОЕНИЕ
1.
2. ДОКАЗАТЕЛЬСТВО
3. P AMK B= AM+MK+KB
4. AM AM=A1K
5. ломаная AMKB – искомая
P AMKB=A1K+MK+KB=A1B+MK

ЗАДАЧА №5
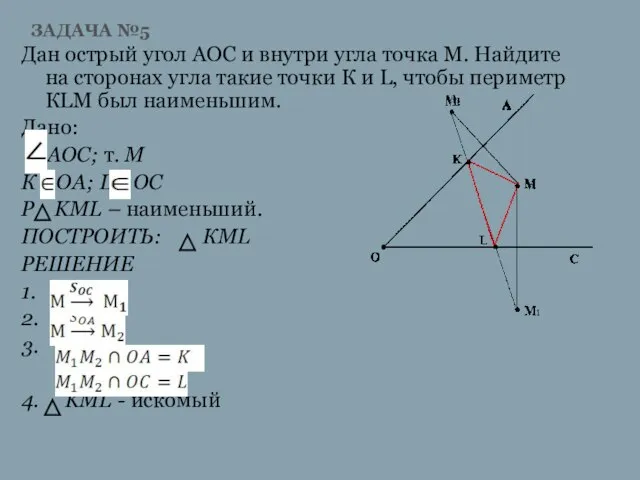
Дан острый угол АОС и внутри угла точка М. Найдите на сторонах угла такие точки К и L, чтобы периметр КLМ был наименьшим.
Дано:
АОС; т. М
К ОА; L OC
P KML – наименьший.
ПОСТРОИТЬ: КМL
РЕШЕНИЕ
1.
2.
3.
4. KML - искомый