Слайд 2Цели и задачи: почему я выбрал эту тему?
Я считаю, что без точки,

прямой, отрезка, луча и угла мы не смогли бы жить. Потому что всё, на что бы не упал наш взгляд , состоит из этих составляющих. Например: книги, техника, орнаменты, деревья, картины, мебель, дома и так далее. Без их участия существуют только окружности и все, у чего нет углов. И я хочу, чтобы все обратили внимание на эти, казалось бы, незначительные вещи.
Слайд 3План презентации:
1.История геометрии ( в двух частях ).
2.Точка, прямая и отрезок:
2.1.Провешивание

прямой на местности
2.2.Пересекающиеся и параллельные прямые.
3.Луч и угол.
3.1.Смежные и вертикальные углы.
3.2.Градусная мера угла
Слайд 4История геометрии. Часть 1.
Евклид (ок. 300 до н.э.)
Греческий математик, чей главный

труд «Начала» остается основой большей части современной геометрии. Одна из известных аксиом Евклидовой геометрии гласит: если дана линия и точка вне ее, то через эту точку можно провести только одну линию, параллельную первой. Эту аксиому нельзя доказать, и попытки заменить ее на другую, по которой через точку вне прямой нельзя провести ни одной линии, параллельной данной, или можно провести множество таких линий, привели к созданию в XIX веке так называемых неевклидовых геометрий ( например, геометрии Лобачевского), которые очень важны для многих сторон современной физики.
Слайд 5История геометрии. Часть 2.
Лобачевский, Николай Иванович (1792-1856).
Русский математик, предложивший заменить один из

главных постулатов геометрии Евклида о параллельных на аксиому, что в плоскости через точку, лежащую вне прямой, можно провести более одной прямой, не пересекающей первую. Это открытие, не получившее признания современников, совершило затем переворот в представлении о природе пространства и оказало огромное влияние на развитие математического мышления.
Слайд 6Точки, прямые и отрезки
Правило: Через любые две точки можно провести только одну
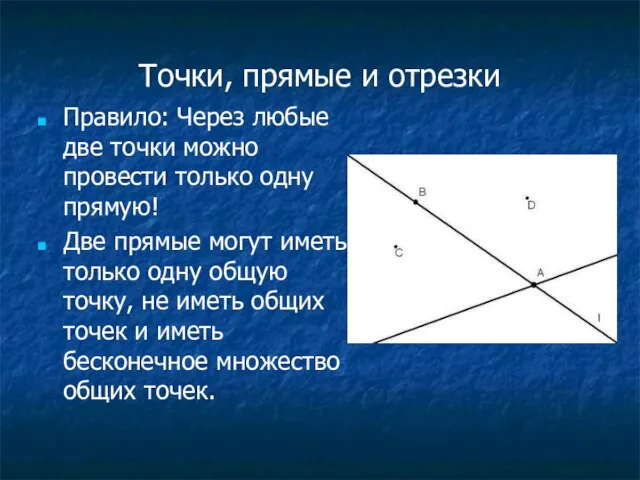
прямую!
Две прямые могут иметь только одну общую точку, не иметь общих точек и иметь бесконечное множество общих точек.
Слайд 7Точка, прямая и отрезок: провешивание прямой на местности.
Когда-то перед людьми встала такая

задача:
Построить отрезок большей длины, чем сама вещь, отрезок которой строили.
Как вышли из положения:
просто приложили к листу бумаги линейку, отметили какие-нибудь точки A и B и лежащею между ними точку C. Затем они передвинули линейку вправо так, чтобы ее левый конец оказался около точки C, и отметили точку D около правого конца линейки. Такой прием называется провешиванием прямой на плоскости.
Слайд 8Пересекающиеся и параллельные прямые
Существуют пересекающиеся и параллельные прямые.
Пересекающимися называют линии, которые имеют

хотя бы одну общую точку.
Параллельными прямыми называют линии, не имеющие ни одной общей точки.
Слайд 9Углы
Угол называется развернутым, если обе его стороны лежат на одной прямой. Если

угол неразвернутый, то одна из частей называется внутренней, а другая – внешней областью. Таким образом, точки A,B,F,I,M лежат на внешней области угла, а точки D,C на внутренней области. Точка E лежит на самом углу.








 Трапеция
Трапеция Угол. Виды углов
Угол. Виды углов Линейные пространства и линейные операторы. Лекция 5
Линейные пространства и линейные операторы. Лекция 5 Сложение и вычитание. Скобки
Сложение и вычитание. Скобки Функции. 8 класс
Функции. 8 класс Относительные показатели: динамики, плана, координации
Относительные показатели: динамики, плана, координации Экспедиция в страну дроби
Экспедиция в страну дроби Формулы комбинаторики. Формула числа перестановок, размещений и сочетаний
Формулы комбинаторики. Формула числа перестановок, размещений и сочетаний Несобственные интегралы. Лекция 5
Несобственные интегралы. Лекция 5 Мишка. Тренажёр - раскраска
Мишка. Тренажёр - раскраска определение и свойства числ.функции
определение и свойства числ.функции Сумма n первых членов геометрической прогрессии (9 класс)
Сумма n первых членов геометрической прогрессии (9 класс) Конус. Цилиндр. Сфера
Конус. Цилиндр. Сфера الأعداد انسبية
الأعداد انسبية Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Презентация на тему Методы решений тригонометрических уравнений
Презентация на тему Методы решений тригонометрических уравнений  Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Презентация на тему Решение квадратных уравнений и неравенств
Презентация на тему Решение квадратных уравнений и неравенств  Презентация на тему Римские цифры (3 класс)
Презентация на тему Римские цифры (3 класс)  Сантиметр - единица измерения длины
Сантиметр - единица измерения длины Окружность Аполлония
Окружность Аполлония Ознакомление с составной задачей
Ознакомление с составной задачей Золотое сечение. 9 класс
Золотое сечение. 9 класс мощность множеств Леонгардт
мощность множеств Леонгардт Квадратичная функция. Парабола
Квадратичная функция. Парабола Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами Построение треугольника
Построение треугольника Задачи про виноград и изюм. ЕГЭ. Профильный уровень
Задачи про виноград и изюм. ЕГЭ. Профильный уровень