Оценка сложных систем в условиях неопределенности

Специфические черты организационно-технических систем
1. Наличие в управляемой системе в качестве элементов (подсистем) целенаправленных индивидуумов и наличие в системе управления ЛПР,
2. Алгоритм управления часто строит сама система управления, преследуя помимо предъявляемых старшей системой целей, собственные цели, не всегда совпадающие с внешними.
3. На этапе оценки ситуации в ряде случаев исходят не из фактической ситуации, а из той модели, которой пользуется ЛПР при управлении объектом.
4. В процессе принятия решения большую роль играют логические рассуждения ЛПР, не поддающиеся формализации классическими методами математики.
5. При выборе управляющего воздействия ЛПР может оперировать нечеткими понятиями, отношениями и высказываниями.
6. В большом классе задач управления организационно-техническими системами отсутствуют объективные критерии оценивания достижения целевого и текущего состояний объекта управления

Оценка эффективности для неопределенных операций

Критерий среднего выигрыша
Данный критерий предполагает задание вероятностей состояний обстановки pi. Эффективность систем оценивается как среднее ожидаемое значение (математическое ожидание) оценок эффективности по всем состояниям обстановки:
Оптимальной системе будет соответствовать эффективность
Если в данном примере задаться вероятностями применения противником программных воздействий p1=0,4; p2=0,2; p3=0,1; p4=0,3; то получим следующие оценки систем:
K(a1)=0,4*0,1+0,2*0,5+0,1*0,1+0,3*0,2=0,21
K(a2)=0,4*0,2+0,2*0,3+0,1*0,2+0,3*0,4=0,28
K(a3)=0,4*0,1+0,2*0,4+0,1*0,4+0,3*0,3=0,25
Оптимальное решение - система a2.

Критерий Лапласа
В основе критерия лежит предположение: поскольку о состояниях обстановки ничего не известно, то их можно считать равновероятными.
Исходя из этого
Рассчитаем эффективность систем по данному критерию для приведенного примера:
K(a1)=0,25*(0,1+0,5+0,1+0,2)=0,225
K(a2)=0,25*(0,2+0,3+0,2+0,4)=0,275
K(a3)=0,25*(0,1+0,4+0,4+0,3)=0,3
Оптимальное решение - система a3. Критерий Лапласа представляет собой частный случай критерия среднего выигрыша.

Критерий осторожного наблюдателя (Вальда)
Это максиминный критерий, он гарантирует определенный выигрыш при наихудших условиях.
В каждой строке матрицы эффективности находится минимальная из оценок систем по различным состояниям обстановки
Применение критерия максимина к нашему примеру дает следующие оценки:
К(а1) = min(0,l; 0,5; 0,1; 0,2) = 0,1;
К(а2) = min(0,2; 0,3; 0,2; 0,4) = 0,2;
К(а3) = min(0,1; 0,4; 0,4; 0,3) = 0,1;
Оптимальное решение - система а2.
Максиминный критерий ориентирует на решение, не содержащее элементов риска: при любом из возможных состояний обстановки выбранная система покажет результат операции не хуже найденного максимина.

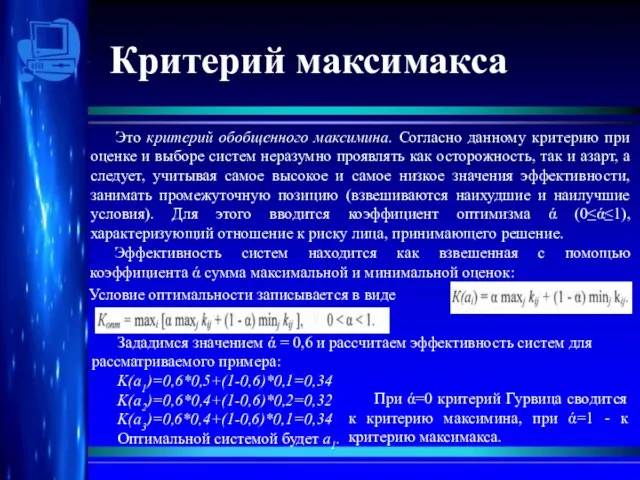
Критерий максимакса
Это критерий обобщенного максимина. Согласно данному критерию при оценке и выборе систем неразумно проявлять как осторожность, так и азарт, а следует, учитывая самое высокое и самое низкое значения эффективности, занимать промежуточную позицию (взвешиваются наихудшие и наилучшие условия). Для этого вводится коэффициент оптимизма ά (0≤ά≤1), характеризующий отношение к риску лица, принимающего решение.
Эффективность систем находится как взвешенная с помощью коэффициента ά сумма максимальной и минимальной оценок:
Условие оптимальности записывается в виде
Зададимся значением ά = 0,6 и рассчитаем эффективность систем для рассматриваемого примера:
K(a1)=0,6*0,5+(1-0,6)*0,1=0,34
K(a2)=0,6*0,4+(1-0,6)*0,2=0,32
K(a3)=0,6*0,4+(1-0,6)*0,1=0,34
Оптимальной системой будет а1.
При ά=0 критерий Гурвица сводится к критерию максимина, при ά=1 - к критерию максимакса.

Критерий минимального риска (Сэвиджа)
Минимизирует потери эффективности при наихудших условиях. Для оценки систем на основе данного критерия матрица эффективности должна быть преобразована в матрицу потерь (риска). Каждый элемент матрицы потерь определяется как разность между максимальным и текущим значениями оценок эффективности в столбце:Δkij=maxikij-kij
После преобразования матрицы используется критерий минимакса:
K(ai)=maxj Δkij
Kopt=mini(maxj Δkij)
Матрица потерь
K(a1)=max(0,1;0;0,3;0,2)=0,3
K(a2)=max(0;0,2;0,2;0)=0,2
K(a3)=max(0,1;0,1;0;0,1)=0,1
Оптимальное решение - система аз.
Критерий минимального риска отражает сожаление по поводу того, что выбранная система не оказалась наилучшей при определенном состоянии обстановки.

Сравнительные результаты оценки систем
Эффективность систем в неопределенных операциях может оцениваться по целому ряду критериев. На выбор того или иного критерия оказывает влияние ряд факторов:
природа конкретной операции и ее цель (в одних операциях допустим риск, в других нужен гарантированный результат);
причины неопределенности (одно дело, когда неопределенность является случайным результатом действия объективных законов природы, и другое, когда она вызывается действиями разумного противника, стремящегося помешать в достижении цели);
характер лица, принимающего решение (одни люди склонны к риску в надежде добиться большего успеха, другие предпочитают действовать всегда осторожно).

Литература
Ю.П.Сурмин «Теория систем и системный анализ»
В.С.Анфилатов, А.А.Емельянов, А.А.Кукушкин «Системный анализ в управлении»
Т.П.Барановская, В.И.Лойко, М.И.Семёнов, А.И.Трубилин «Информационные системы и технологии в экономике»
В.К.Душин «Теоретические основы информационных процессов и систем»
М.Месарович, Я.Такахара «Общая теория систем»
А.В. «Теория информационных процессов и систем» http://www.studfiles.ru/dir/cat32/subj418/file14036.html