- Главная
- Математика
- Презентация на тему Возрастание и убывание функций

Содержание
- 2. Познакомимся на примере с возрастанием и убыванием функции. На рисунке ниже изображен график функции, определенной на
- 3. Возрастание и убывание четных функций Для четных функций задача нахождения промежутков возрастания и убывания сильно упрощается.
- 4. Возрастание и убывание функции синус Докажем, что синус возрастает на промеждутках [-π/2+2πn ; π/2+2πn], n -
- 5. Возрастание и убывание функции косинус Промежутками возрастания косинуса являются отрезки [-π+2πn ; 2πn], n - целое.
- 6. Упражнение №82а
- 7. Упражнение №82б
- 8. Упражнение №82в
- 9. Упражнение №82г
- 10. Упражнение №83а
- 11. Упражнение №83в
- 12. Упражнение №77,78
- 14. Скачать презентацию
Слайд 2Познакомимся на примере с возрастанием и убыванием функции. На рисунке ниже изображен
Познакомимся на примере с возрастанием и убыванием функции. На рисунке ниже изображен
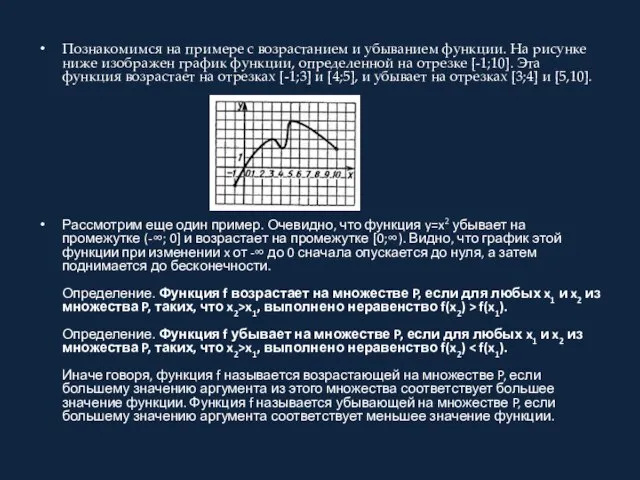
график функции, определенной на отрезке [-1;10]. Эта функция возрастает на отрезках [-1;3] и [4;5], и убывает на отрезках [3;4] и [5,10].
Рассмотрим еще один пример. Очевидно, что функция y=x2 убывает на промежутке (-∞; 0] и возрастает на промежутке [0;∞). Видно, что график этой функции при изменении x от -∞ до 0 сначала опускается до нуля, а затем поднимается до бесконечности. Определение. Функция f возрастает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) > f(x1). Определение. Функция f убывает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) < f(x1). Иначе говоря, функция f называется возрастающей на множестве P, если большему значению аргумента из этого множества соответствует большее значение функции. Функция f называется убывающей на множестве P, если большему значению аргумента соответствует меньшее значение функции.
Рассмотрим еще один пример. Очевидно, что функция y=x2 убывает на промежутке (-∞; 0] и возрастает на промежутке [0;∞). Видно, что график этой функции при изменении x от -∞ до 0 сначала опускается до нуля, а затем поднимается до бесконечности. Определение. Функция f возрастает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) > f(x1). Определение. Функция f убывает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) < f(x1). Иначе говоря, функция f называется возрастающей на множестве P, если большему значению аргумента из этого множества соответствует большее значение функции. Функция f называется убывающей на множестве P, если большему значению аргумента соответствует меньшее значение функции.
Слайд 3Возрастание и убывание четных функций
Для четных функций задача нахождения промежутков возрастания и
Возрастание и убывание четных функций
Для четных функций задача нахождения промежутков возрастания и

убывания сильно упрощается. Достаточно всего лишь найти промежутки возрастания и убывания при x≥0 (см. рисунок внизу).
Пусть, например, функция f четна и возрастает на промежутке [a;b], где b>a≥0. Докажем, что эта функция убывает на промежутке [-b; -a].
Действительно, пусть -a≥x2>x1≥-b. Тогда f(-x2)=f(x2), f(-x1)=f(x1), причем a≤-x2<-x1≤b, и, поскольку f возрастает на [a;b], имеем f(-x1)>f(-x2), то есть f(x1)>f(x2).
Слайд 4Возрастание и убывание функции синус
Докажем, что синус возрастает на промеждутках [-π/2+2πn ;
Возрастание и убывание функции синус
Докажем, что синус возрастает на промеждутках [-π/2+2πn ;

π/2+2πn], n - целое. В силу периодичности функции синуса доказательство достаточно провести для отрезка [-π/2 ; π/2]. Пусть x2 > x1. Применим формулу разности синусов и найдем:
Из неравенства -π/2 ≤ x1 < x2 ≤ π/2 следует, что и , поэтому и , следовательно и .
Это доказывает, что на указанных промежутках синус возрастает.
Аналогичным образом легко доказать, что промежутки [π/2+2πn ; 3π/2+2πn], n - целое, являются промежутками убывания функции синуса.
Полученный результат можно легко проиллюстрировать с помощью рисунка единичной окружности (см. рисунок ниже). Если -π/2 ≤ t1 < t2 ≤ π/2, то точка Pt2 имеет ординату большую, чем точка Pt1. Если же π/2 ≤ t1 < t2 ≤ 3π/2, то ордината точки Pt2 меньше, чем ордината точки Pt1.
Слайд 5Возрастание и убывание функции косинус
Промежутками возрастания косинуса являются отрезки [-π+2πn ;
Возрастание и убывание функции косинус
Промежутками возрастания косинуса являются отрезки [-π+2πn ;

2πn], n - целое. Промежутками убывания косинуса являются отрезки [2πn ; π + 2πn], n - целое. Доказательство этих утверждений можно провести аналогично доказательству для синуса.
Однако, проще воспользоваться формулой приведения cos(x) = sin(x + π/2), из которой сразу следует, что промежутками возрастания косинуса являются промежутки возрастания синуса, сдвинутые на π/2 влево. Аналогичное утверждение можно сделать и для промежутков убывания.
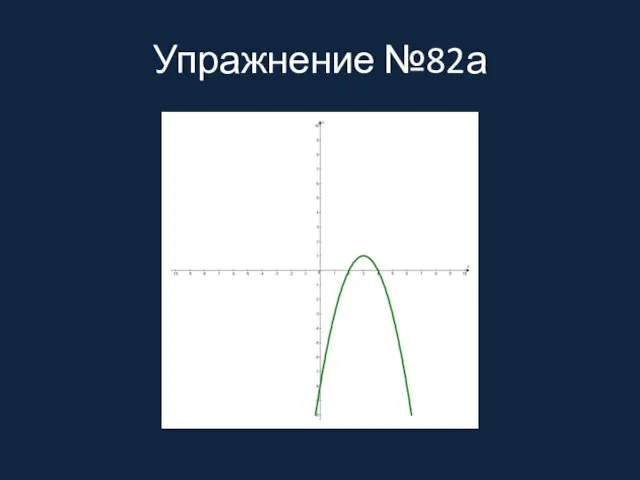
Слайд 6Упражнение №82а
Упражнение №82а
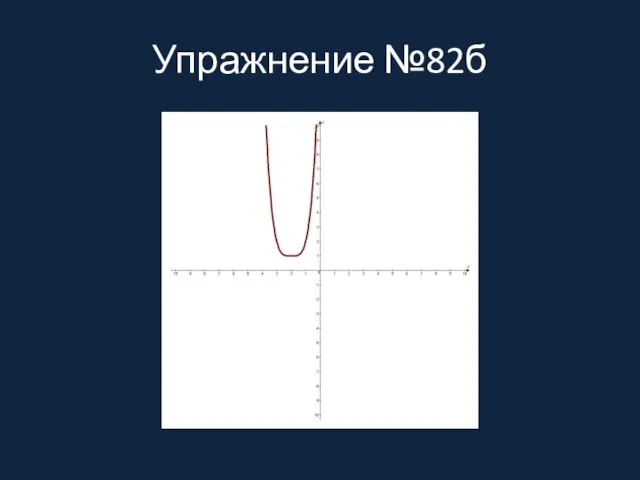
Слайд 7Упражнение №82б
Упражнение №82б
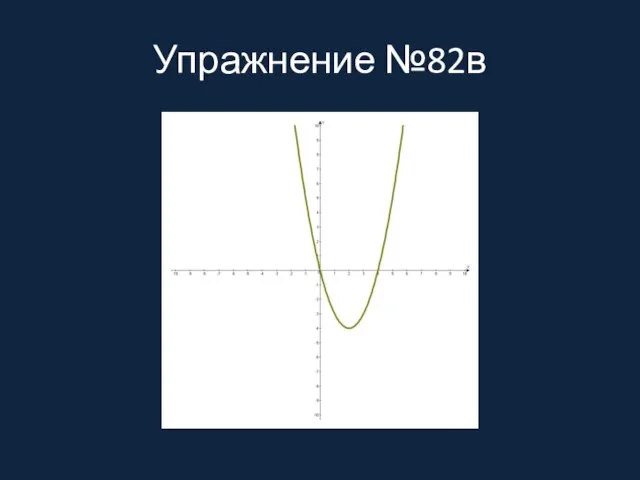
Слайд 8Упражнение №82в
Упражнение №82в
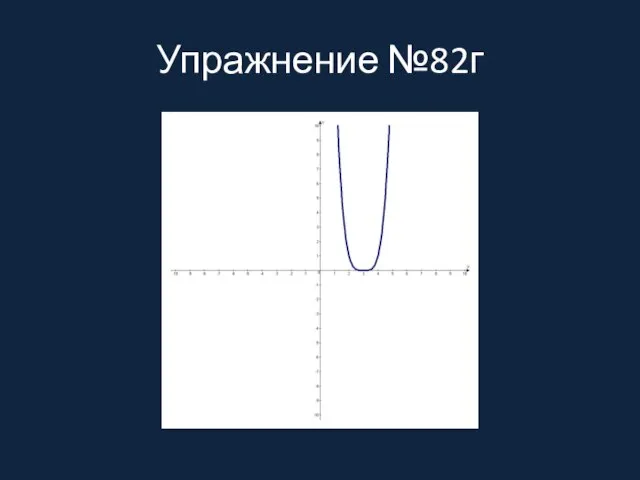
Слайд 9Упражнение №82г
Упражнение №82г
Слайд 10Упражнение №83а
Упражнение №83а

Слайд 11Упражнение №83в
Упражнение №83в

Слайд 12Упражнение №77,78
Упражнение №77,78

 Одночлен. Умножение
Одночлен. Умножение Первый признак равенства треугольников
Первый признак равенства треугольников Методы расчета ферм
Методы расчета ферм Теория динамических систем
Теория динамических систем Презентация на тему Логарифмическая линия в ЕГЭ - 2011
Презентация на тему Логарифмическая линия в ЕГЭ - 2011  Конфетное вычитание
Конфетное вычитание Проект Математическая вертикаль. Геометрия. 8 класс
Проект Математическая вертикаль. Геометрия. 8 класс I признак подобия треугольников
I признак подобия треугольников Решение треугольников
Решение треугольников Примеры арифметических операций при помощи стандартных функций
Примеры арифметических операций при помощи стандартных функций Презентация на тему Арифметические действия с дробями
Презентация на тему Арифметические действия с дробями  Знакомство с линиями чертежа. Наклонная
Знакомство с линиями чертежа. Наклонная Счет
Счет Первообразная и интеграл
Первообразная и интеграл Рациональные числа 6 класс - Презентация по математике_
Рациональные числа 6 класс - Презентация по математике_ Набор инсулина в шприц
Набор инсулина в шприц Занимательная математика
Занимательная математика Основы математического моделирования. Лекция 2
Основы математического моделирования. Лекция 2 Презентация на тему Функция у=кх2 ,ее свойства и график
Презентация на тему Функция у=кх2 ,ее свойства и график  Основные этапы исследования элементарных функций
Основные этапы исследования элементарных функций Бесконечность
Бесконечность Чирмешән муниципаль районы Лашман урта гомумбелем бирү мәктәбе
Чирмешән муниципаль районы Лашман урта гомумбелем бирү мәктәбе двугранный угол. перпендикулярные плоскости. признак
двугранный угол. перпендикулярные плоскости. признак Арифметический корень степени n
Арифметический корень степени n Презентация на тему ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ПЛОСКИЕ ФИГУРЫ
Презентация на тему ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ПЛОСКИЕ ФИГУРЫ  Сравнение двух прогрессий
Сравнение двух прогрессий Задачи на движение
Задачи на движение Координаты вокруг нас
Координаты вокруг нас