Содержание
- 2. Эйлер утверждал, что давление в центрах Солнца или Земли стремятся к нулю. Уравнение гидродинамики, которым пользуются
- 3. Леонард Эйлер Леонард Эйлер ( 15 апреля 1707, Швейцария – 18 сентября 1783, Российская империя, Санкт-Петербург)
- 4. Первая красавица Тождество Эйлера является следствием формул Эйлера, связывающих экспоненту комплексного числа с тригонометрическими функциями. Эта
- 5. Вторая красавица В простейшем случае эта формула связывает между собой количество вершин (V), ребер (E) и
- 6. Третья красавица Тождество Эйлера является частным случаем, если вместо x подставить «пи». Формула Эйлера
- 7. Мы предполагаем ,что эта формула – 4 красавица Эйлера dp/dr=-rho*g+2p/r Где 2p/r – мы назовем слагаемым
- 8. Выводы 1. Мы получили расширенную теорему о вириале. 2. Мы заметили, что при изменении радиуса температура
- 10. H – энтальпия, играет роль внутренней энергии в изобарных процессах. H = U + pV. Сумма
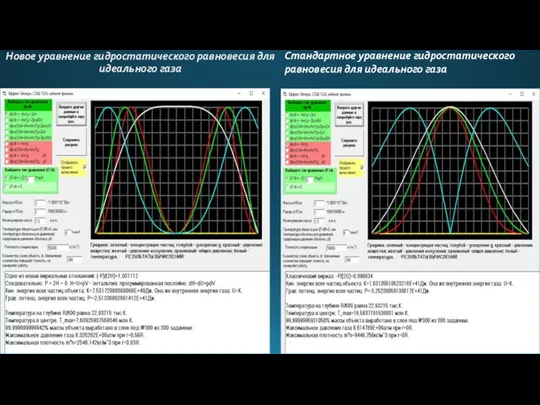
- 11. Новое уравнение гидростатического равновесия для идеального газа Стандартное уравнение гидростатического равновесия для идеального газа
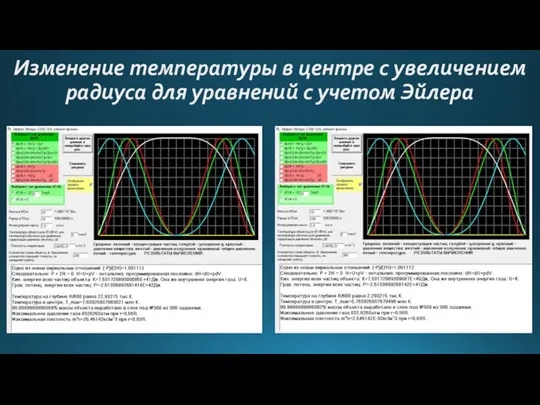
- 12. Изменение температуры в центре с увеличением радиуса для уравнений с учетом Эйлера
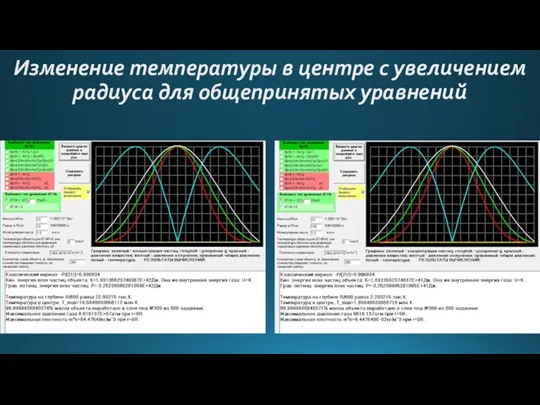
- 13. Изменение температуры в центре с увеличением радиуса для общепринятых уравнений
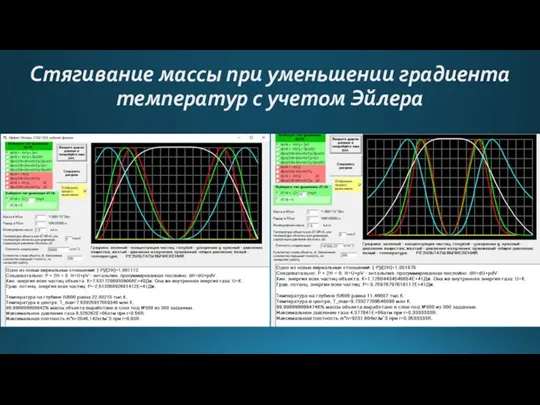
- 14. Стягивание массы при уменьшении градиента температур с учетом Эйлера
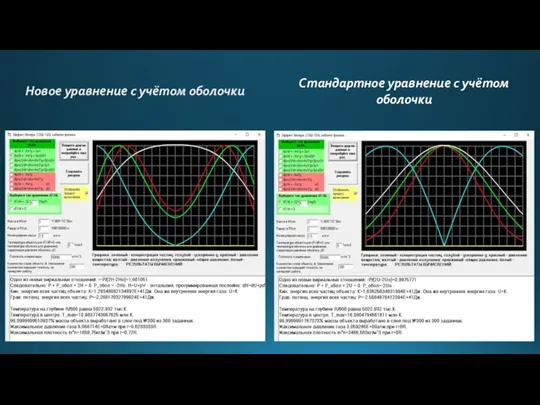
- 15. Новое уравнение с учётом оболочки Стандартное уравнение с учётом оболочки
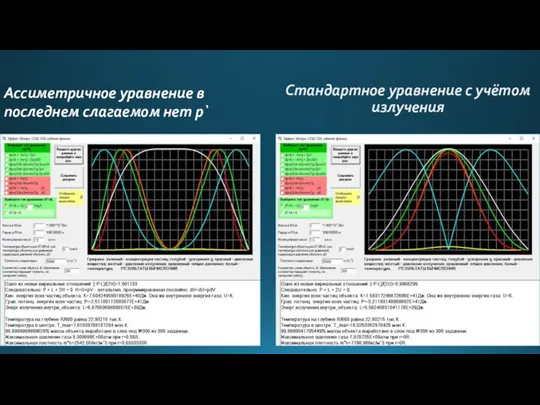
- 16. Стандартное уравнение с учётом излучения Ассиметричное уравнение в последнем слагаемом нет p`
- 18. Скачать презентацию








 Решение задач. Диагностика 1
Решение задач. Диагностика 1 Математический диктант. 6 класс
Математический диктант. 6 класс Числовые ряды
Числовые ряды Соотношение числа и цифры. Считаем от 1 до 9
Соотношение числа и цифры. Считаем от 1 до 9 Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма
Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма Повторим правила образования и записи чисел
Повторим правила образования и записи чисел Диофантово уравнение
Диофантово уравнение Векторы
Векторы Задачі_на_наслідки_із_аксіом_стереометрії
Задачі_на_наслідки_із_аксіом_стереометрії Числовые головоломки
Числовые головоломки 6cc84cfba09801fa77f2178065bede8f
6cc84cfba09801fa77f2178065bede8f Методы оптимизации. Ограничения в виде равенств и неравенств
Методы оптимизации. Ограничения в виде равенств и неравенств Наибольший общий делитель (НОД) и наименьшее общее кратное чисел (НОК)
Наибольший общий делитель (НОД) и наименьшее общее кратное чисел (НОК) Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка
Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка Regresní a korelační analýza
Regresní a korelační analýza Предел функции (часть 2)
Предел функции (часть 2)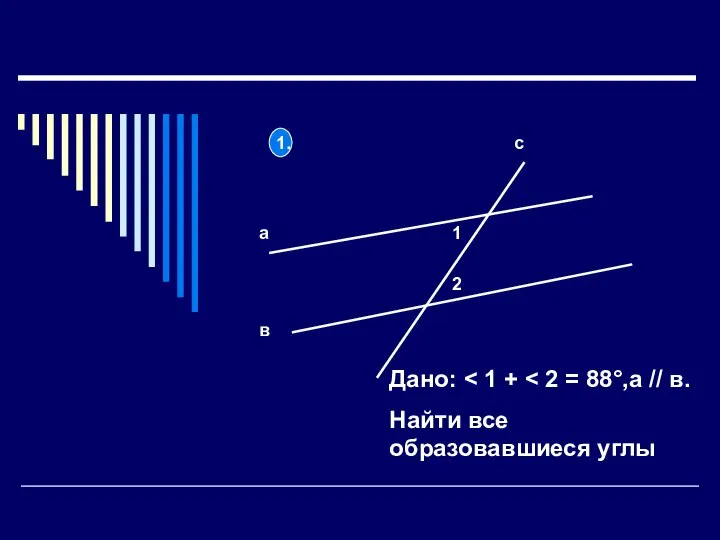 Признаки равенства треугольников
Признаки равенства треугольников Угол между прямой и плоскостью. Теорема о трёх перпендикулярах
Угол между прямой и плоскостью. Теорема о трёх перпендикулярах Подготовка к ЕГЭ (профильный уровень). Задания 5
Подготовка к ЕГЭ (профильный уровень). Задания 5 Уравнения и неравенства в целых числах
Уравнения и неравенства в целых числах Теорема Виета. Устная работа
Теорема Виета. Устная работа Минимизация переключательных функций
Минимизация переключательных функций Прямая и плоскость в пространстве. Лекция 6
Прямая и плоскость в пространстве. Лекция 6 Таблица умножения девяти. Тренажёр-раскраска
Таблица умножения девяти. Тренажёр-раскраска Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Методика изучения одномерных геометрических фигур в курсе математики начальных классов: точка, линия, прямая
Методика изучения одномерных геометрических фигур в курсе математики начальных классов: точка, линия, прямая Диаграммы Ламерея. Качественный анализ дискретных ДС
Диаграммы Ламерея. Качественный анализ дискретных ДС Сложение десятичных дробей
Сложение десятичных дробей