Слайд 2Типы заданий
Геометрический смысл производной
Касательная в точке
Механический смысл производной
Промежутки возрастания-убывания
Локальные экстремумы
Наибольшие/наименьшие значения на

отрезке
Слайд 3Геометрический смысл производной (теория)
Следующие величины равны
Значение производной f’(x0) в точке x0
Тангенс угла

наклона касательной к графику функции y= f (x0) в точке x0
Угловой коэффициент касательной к графику функции y= f (x0) в точке x0
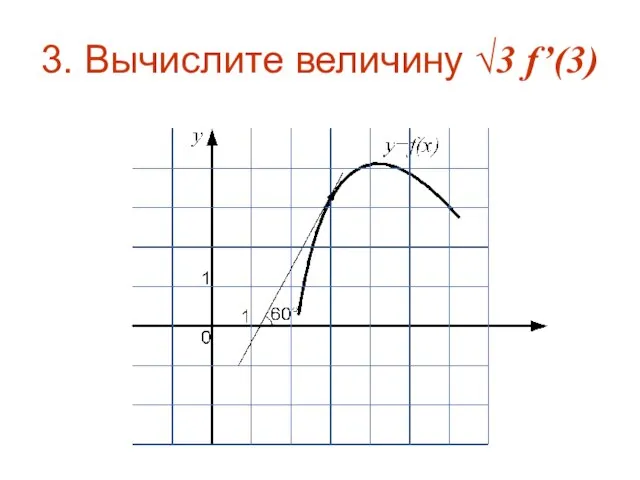
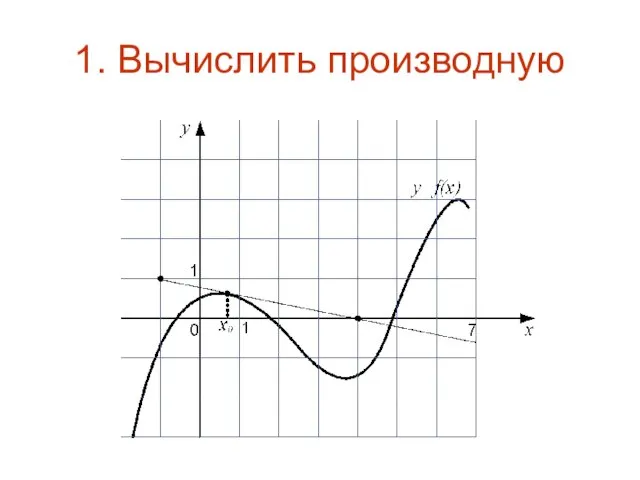
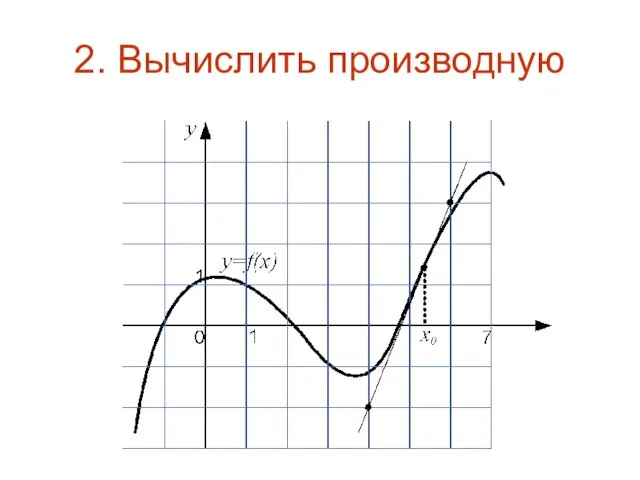
Слайд 63. Вычислите величину √3 f’(3)
Слайд 74. Точка касания
На рисунке изображен график производной функции y= f (x). Прямая
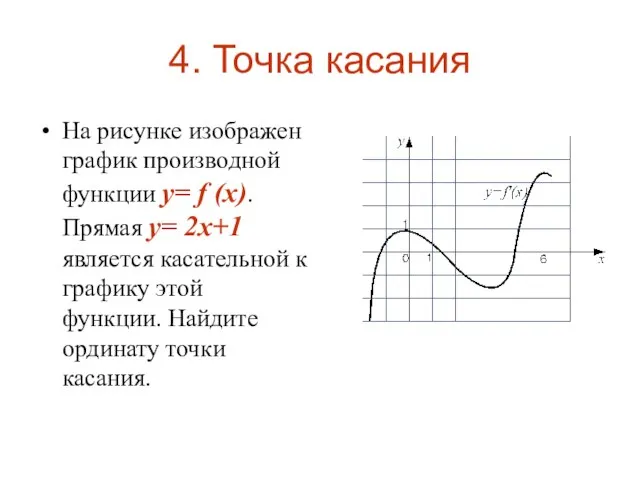
y= 2x+1 является касательной к графику этой функции. Найдите ординату точки касания.
Слайд 85. Точка касания
На рисунке изображен график производной функции y= f (x). Прямая
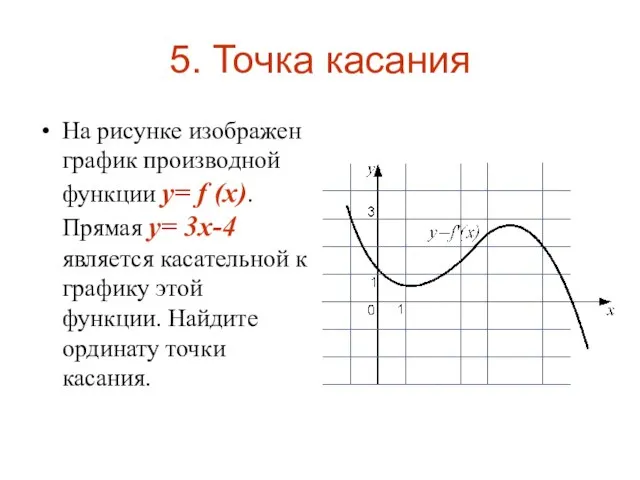
y= 3x-4 является касательной к графику этой функции. Найдите ординату точки касания.
Слайд 9Задачи 6-8
Касательная к графику функции y= 3 – 2x – x2 параллельна

прямой y= 4x. Найдите абсциссу точки касания.
Касательная к графику функции y= 3 – 2x – x2 проходит через точки А(1, 1) и В(-1, 5). Найдите абсциссу точки касания
Найдите положительное значение параметра b, при котором прямая y= -3 является касательной к графику функции y= 2x2 + bx – 1.
Слайд 10Задачи 9 - 12
Прямая y= x+2 является касательной к графику функции y=

аx2 – х + 6 . Найдите а.
Прямая y= 2x является касательной к графику функции y= - x2 +7х + с . Найдите с.
Прямая y= kx + b является касательной к графику функции y= - x2 +4х - 1 в точке А(1,2). Найдите b.
Касательная к графику функции y= x(x-2) проходит через точки А(1, -2) и В(-3, 6). Найдите ординату точки касания
Слайд 11Механический смысл производной
Если s(t) – функция, задающая закон движения материальной точки (пройденный

путь в зависимости от времени), то v(t)=s’(t) – мгновенная скорость точки
Слайд 12Движение материальной точки
Материальная точка движется прямолинейно по закону s(t)=1/3 t3 + ½

t2 – 9t +1, где s – расстояние от точки отсчета в метрах, а t – время в секундах с начала движения. Через сколько секунд после начала движения скорость точки будет равна 3 м/с?
Материальная точка движется прямолинейно по закону s(t)=6 + 2t – 0,25t2, где s – расстояние от точки отсчета в метрах, а t – время в секундах с начала движения. Через сколько секунд после начала движения точка остановится?
Материальная точка движется прямолинейно по закону s(t)= 4 + 2t – t2, где s – расстояние от точки отсчета в метрах, а t – время в секундах с начала движения. Какова была начальная скорость точки (в м/с)?
Слайд 13Промежутки возрастания-убывания
Определение возрастающей (убывающей) функции на промежутке
Функция является возрастающей на промежутке ↔

когда ее производная положительна в любой точке промежутка
Функция является убывающей на промежутке ↔ когда ее производная отрицательна в любой точке промежутка
Слайд 14Возрастание/убывание
На рисунке изображен график функции y=f(x). Определите количество целых точек на интервале
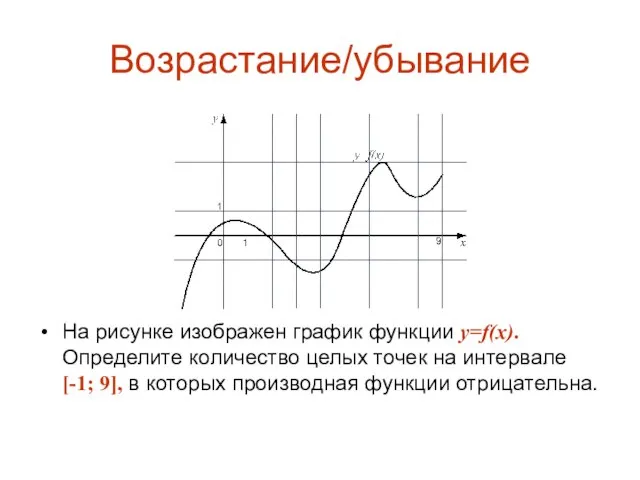
[-1; 9], в которых производная функции отрицательна.
Слайд 15Возрастание/убывание
На рисунке изображен график функции y=f(x). Определите количество целых точек на интервале
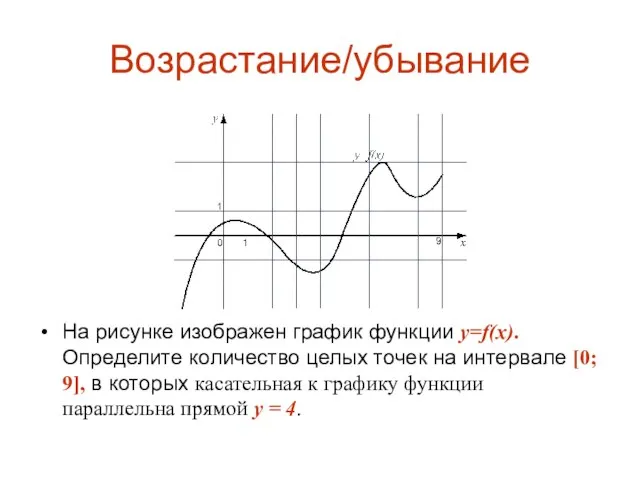
[0; 9], в которых касательная к графику функции параллельна прямой y = 4.
Слайд 16Возрастание/убывание
На рисунке изображен график функции y=f(x). Определите, в какой точке промежутка [5;
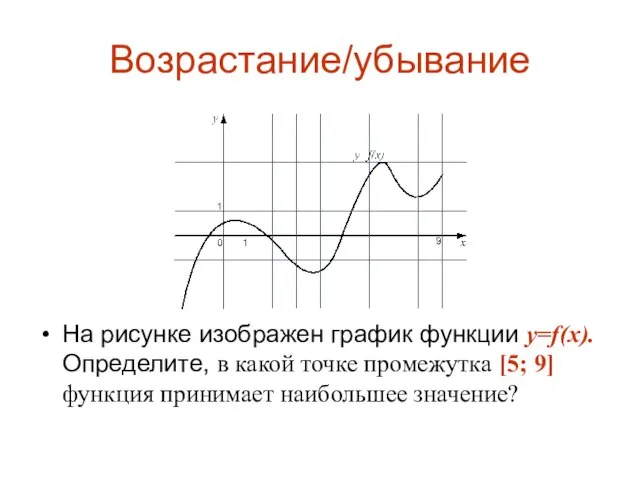
9] функция принимает наибольшее значение?
Слайд 17Возрастание/убывание
На рисунке изображен график производной функции y=f(x). Найдите промежутки возрастания данной функции,
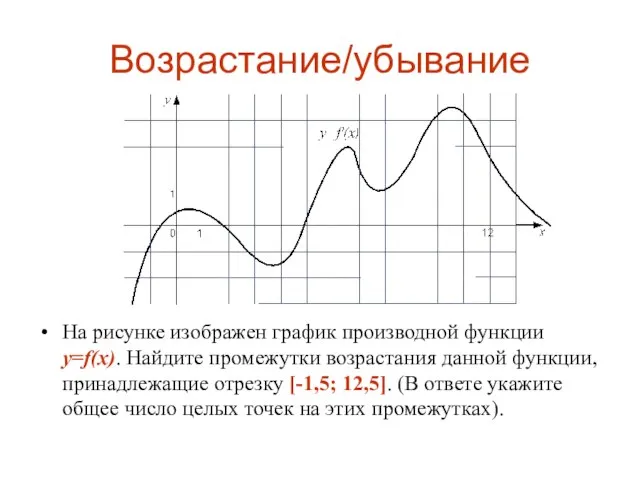
принадлежащие отрезку [-1,5; 12,5]. (В ответе укажите общее число целых точек на этих промежутках).
Слайд 18Возрастание/убывание
На рисунке изображен график производной функции y=f(x). Найдите сумму целочисленных абсцисс точек,
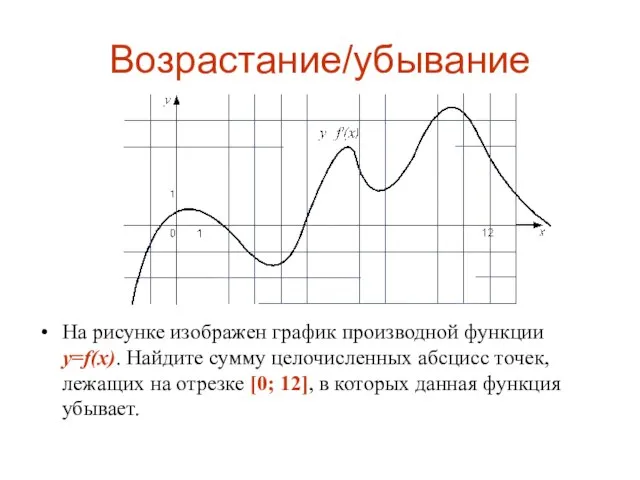
лежащих на отрезке [0; 12], в которых данная функция убывает.
Слайд 19Возрастание/убывание
Найдите количество промежутков убывания функции y=f(x), если ее производная имеет вид
f’(x)

= (x2 – 1)(x2 – 9)(x – 4)2
Слайд 20Локальные экстремумы
Определение максимума (минимума) функции
Точка х0 является точкой максимума функции y=f(x) ,

если f’(x0)=0 и при переходе через эту точку производная меняет знак с плюса на минус.
Точка х0 является точкой минимума функции y=f(x) , если f’(x0)=0 и при переходе через эту точку производная меняет знак с минуса на плюс.
Слайд 21Локальный экстремум
На рисунке изображен график производной функции y=f(x). Найдите целое положительное число
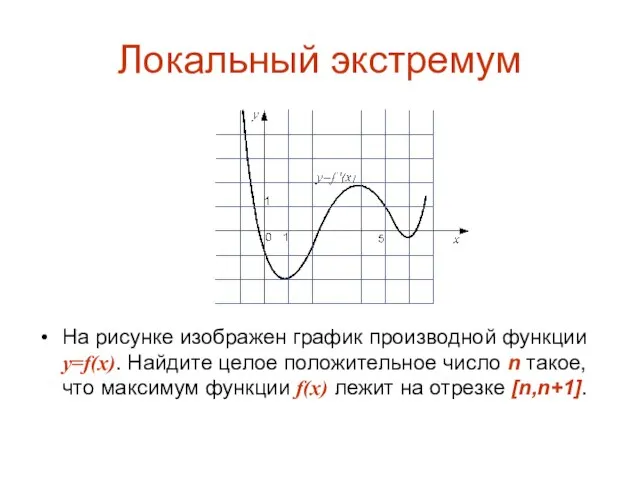
n такое, что максимум функции f(x) лежит на отрезке [n,n+1].
Слайд 22Локальный экстремум
На рисунке изображен график производной функции y=f(x). В точке максимума к
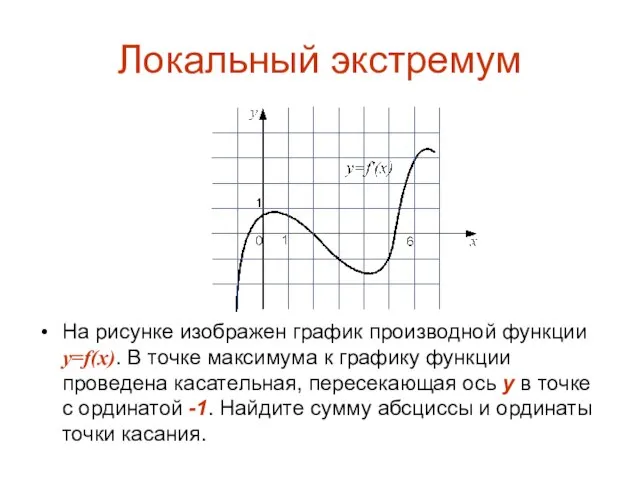
графику функции проведена касательная, пересекающая ось у в точке с ординатой -1. Найдите сумму абсциссы и ординаты точки касания.
Слайд 23Локальный экстремум
На рисунке изображен график производной функции y=f(x). В точке максимума к
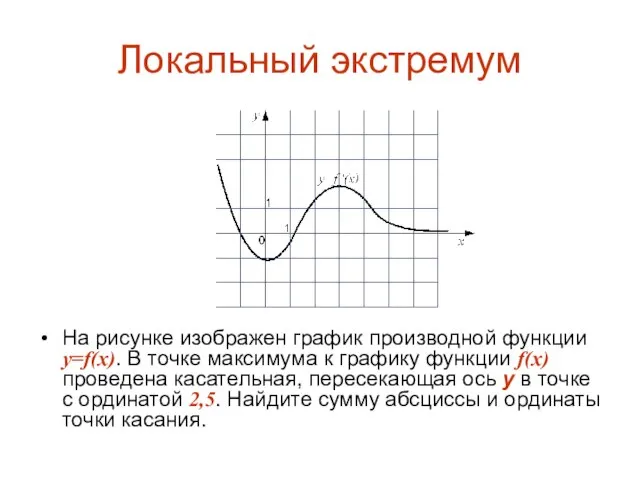
графику функции f(x) проведена касательная, пересекающая ось у в точке с ординатой 2,5. Найдите сумму абсциссы и ординаты точки касания.
Слайд 24Локальный экстремум
На рисунке изображен график производной функции y=f(x). Сколько минимумов имеет данная
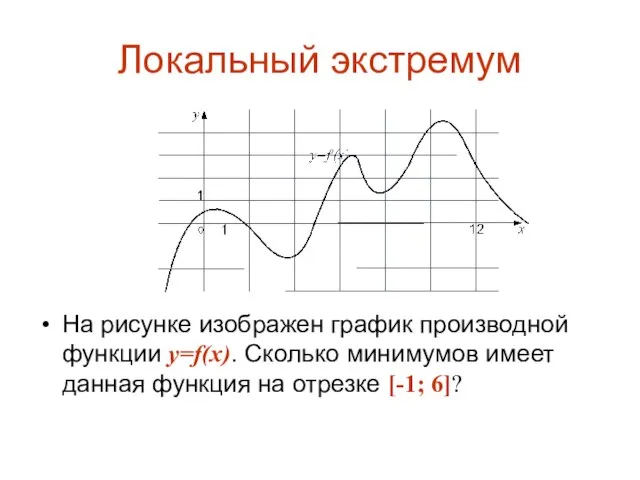
функция на отрезке [-1; 6]?
Слайд 25Локальный экстремум
Найдите количество точек максимума функции y=f(x), если
f’(x) = (x2 +

3x – 4)(x2 – 16)(x2 – 1)
Слайд 26Экстремумы на отрезке
Наибольшее значение функции на отрезке находится как наибольшее из локальных

максимумов и значений на границах
Наименьшее значение функции на отрезке находится как наименьшее из локальных минимумов и значений на границах
Слайд 27Экстремумы на отрезке
Найдите точку, в которой функция
y=2x3 + 9x2 – 60x

+1 принимает наибольшее значение на промежутке
[-6; 6].
Найдите значение функции
y=1/4x4 - 2x2 +5 в точке максимума
Найдите наименьшее значение функции y=π/√3 - √3 x – 2 cosx + 11 на отрезке [0; π/2]
























 Элементы теории множеств. Математические основы информатики
Элементы теории множеств. Математические основы информатики Степенная функция
Степенная функция Замена двузначного числа суммой разрядных слагаемых
Замена двузначного числа суммой разрядных слагаемых Рекурсивные алгоритмы
Рекурсивные алгоритмы Приёмы устных вычислений вида 260+310 670-140
Приёмы устных вычислений вида 260+310 670-140 Начертательная геометрия – это не просто, это очень просто
Начертательная геометрия – это не просто, это очень просто Отрезок, луч, прямая. Графический диктант 1. 5 класс
Отрезок, луч, прямая. Графический диктант 1. 5 класс Координатный луч. Урок 2
Координатный луч. Урок 2 Презентация на тему Изображение пространственных фигур
Презентация на тему Изображение пространственных фигур  Простейшие задачи в координатах
Простейшие задачи в координатах Веселая математика
Веселая математика Выборочное наблюдение
Выборочное наблюдение График квадратичной функции, содержащей переменную под знаком абсолютной величины
График квадратичной функции, содержащей переменную под знаком абсолютной величины Математическое моделирование и оптимальное управление каталитическими процессами в условиях неопределенности
Математическое моделирование и оптимальное управление каталитическими процессами в условиях неопределенности Различия между разными вариантами технологического процесса. Последовательный анализ
Различия между разными вариантами технологического процесса. Последовательный анализ Эконометрика как наука
Эконометрика как наука Математический анализ. Повтор лекций
Математический анализ. Повтор лекций Сумма углов в треугольнике
Сумма углов в треугольнике Применение производной к построению графиков функции
Применение производной к построению графиков функции Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Приёмы устных вычислений
Приёмы устных вычислений Задачи на движение. Нахождение времени. Взаимосвязь между величинами: скорость, время, расстояни
Задачи на движение. Нахождение времени. Взаимосвязь между величинами: скорость, время, расстояни Линейная алгебра Матрицы
Линейная алгебра Матрицы Теорема косинусов
Теорема косинусов Основное свойство дроби. Сокращение дробей
Основное свойство дроби. Сокращение дробей Тренажёр. Табличное умножение. В сказочном лесу
Тренажёр. Табличное умножение. В сказочном лесу Множества и операции над ними
Множества и операции над ними Степень числа с натуральным показателем
Степень числа с натуральным показателем