Презентация на тему Задания В-9 ЕГЭ-2010

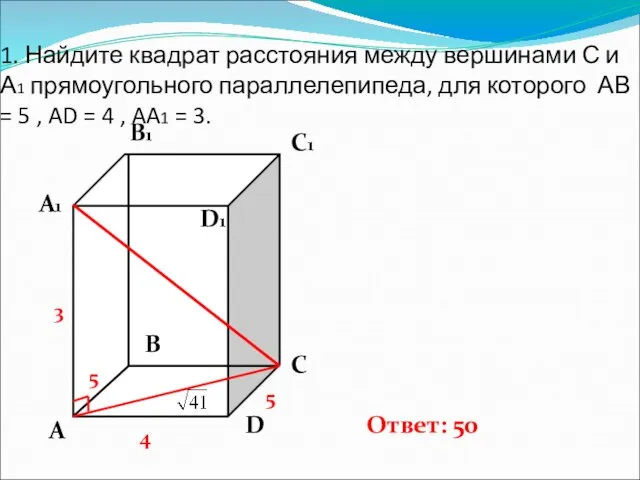
1. Найдите квадрат расстояния между вершинами С и А1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3.
Ответ: 50
4
5
3
5

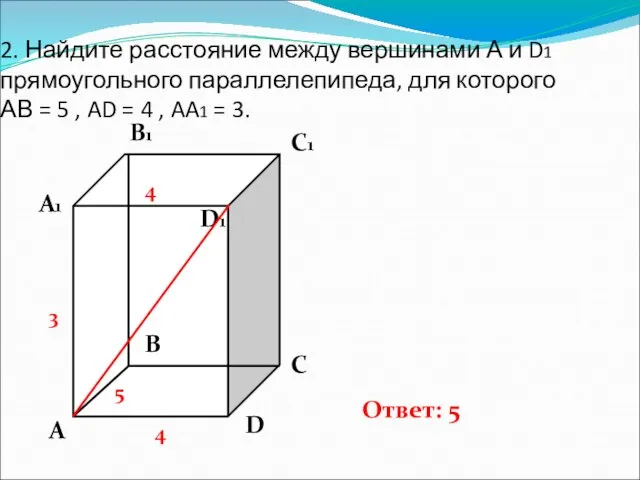
2. Найдите расстояние между вершинами А и D1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3.
Ответ: 5
5
4
3
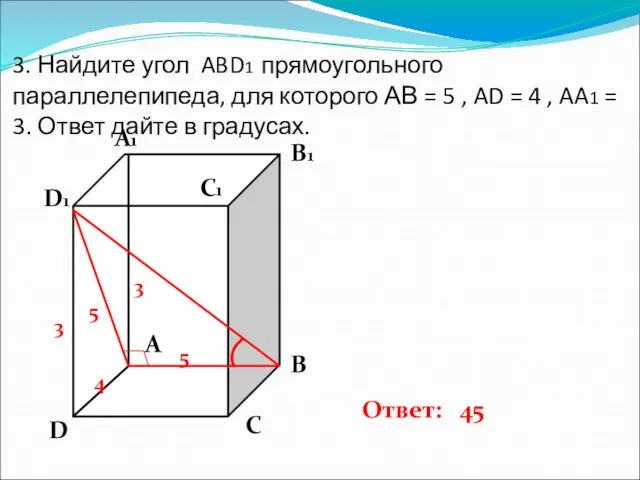
4

3. Найдите угол ABD1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3. Ответ дайте в градусах.
5
4
3
3
5
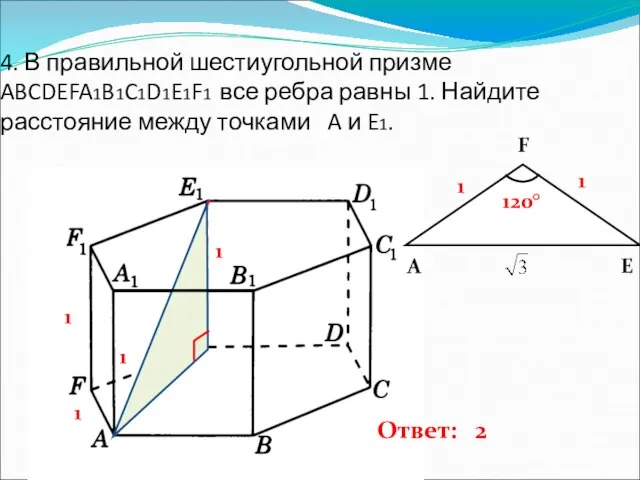
Ответ: 45

4. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками A и E1.
1
1
1
120°
1
Ответ: 2

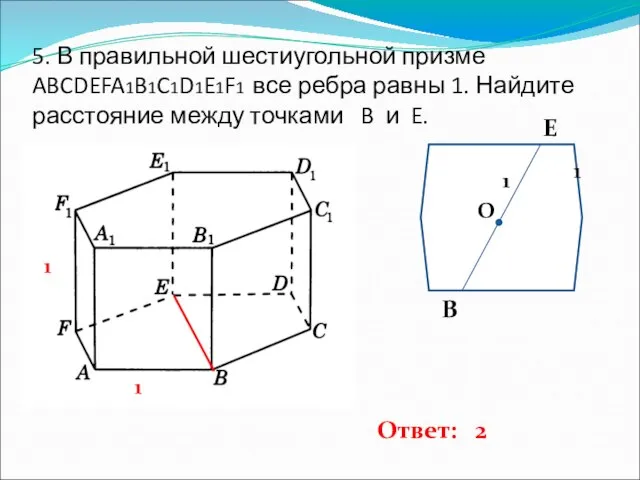
5. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками B и E.
1
1
1
1
Ответ: 2

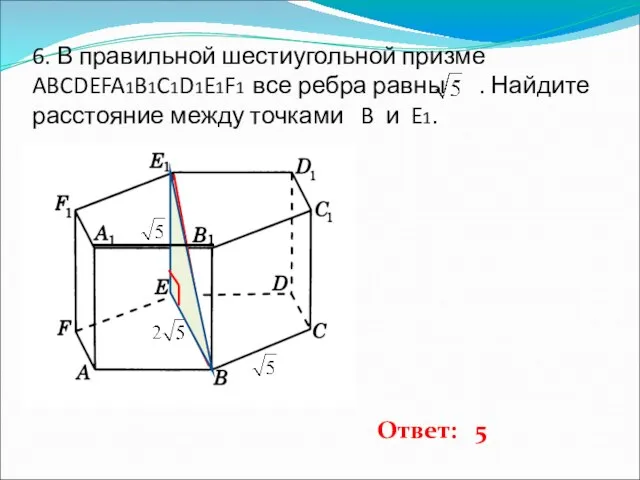
6. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны . Найдите расстояние между точками B и E1.
Ответ: 5

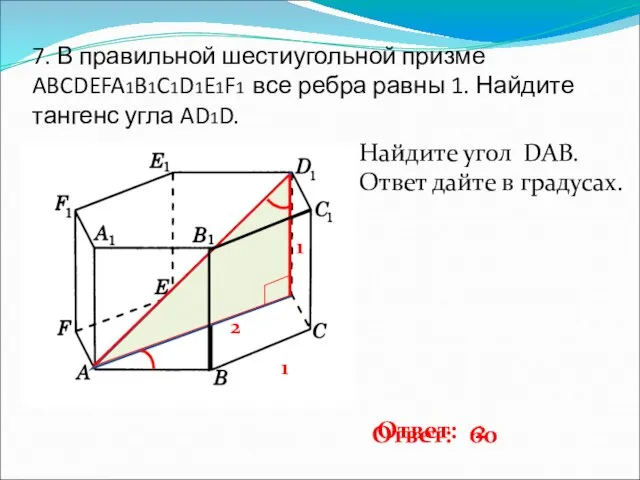
7. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите тангенс угла AD1D.
1
1
2
Ответ: 2
Найдите угол DAB. Ответ дайте в градусах.
Ответ: 60

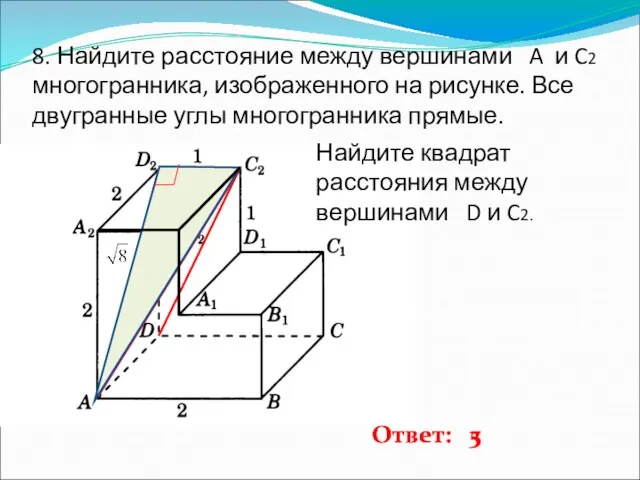
8. Найдите расстояние между вершинами A и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Ответ: 3
Найдите квадрат расстояния между вершинами D и C2.
Ответ: 5

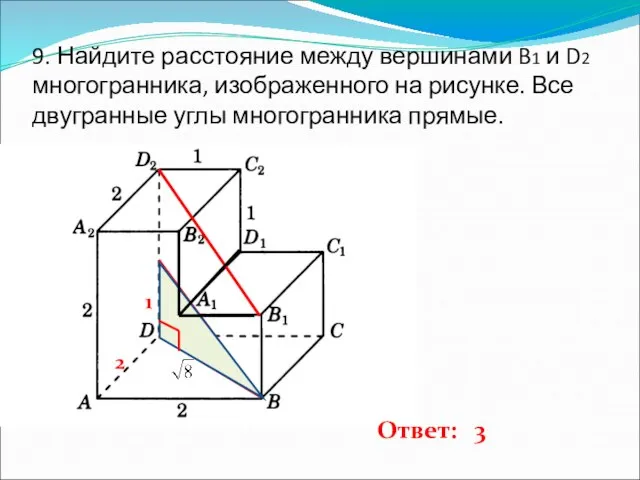
9. Найдите расстояние между вершинами B1 и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
1
2
Ответ: 3

10. Найдите квадрат расстояния между вершинами B и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
1
1
2
Ответ: 14

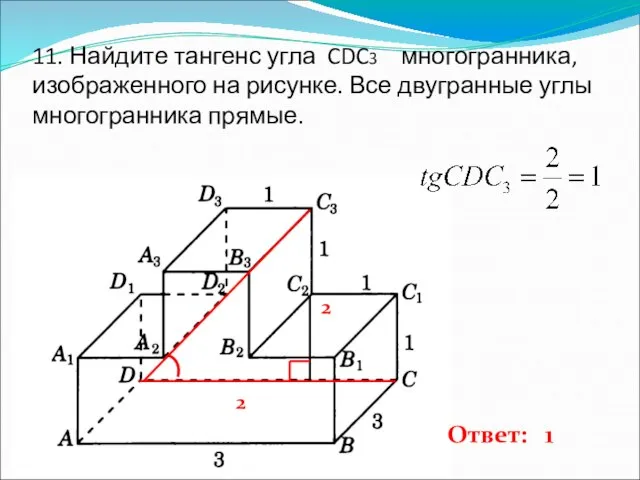
11. Найдите тангенс угла CDC3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
2
2
Ответ: 1

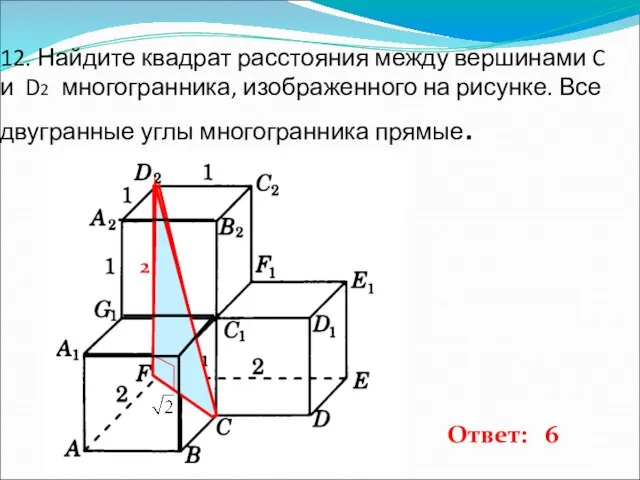
12. Найдите квадрат расстояния между вершинами C и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
2
Ответ: 6

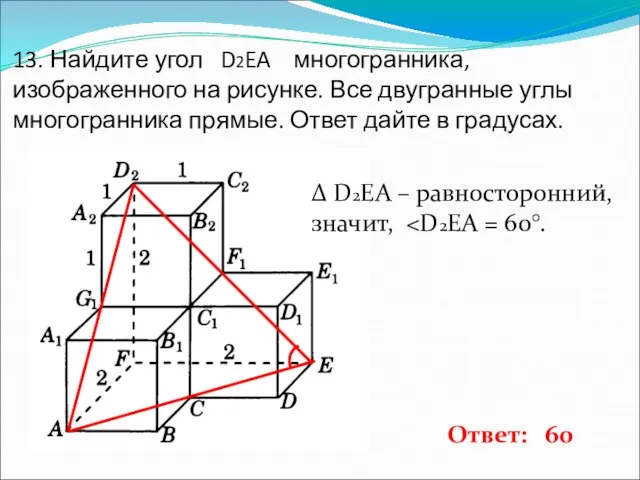
13. Найдите угол D2EA многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Δ D2EA – равносторонний, значит,
Ответ: 60

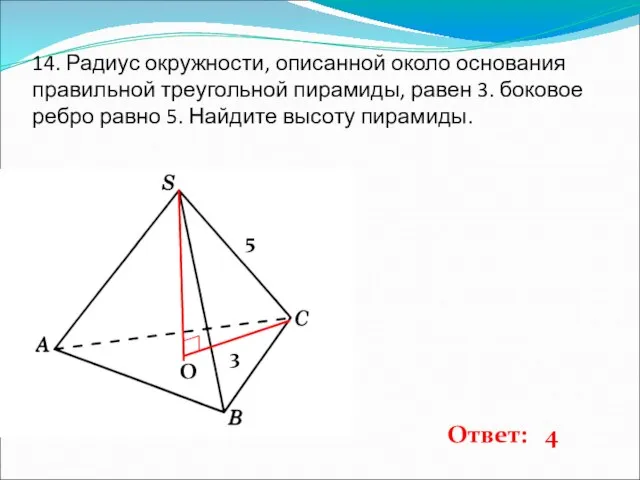
14. Радиус окружности, описанной около основания правильной треугольной пирамиды, равен 3. боковое ребро равно 5. Найдите высоту пирамиды.
3
5
Ответ: 4

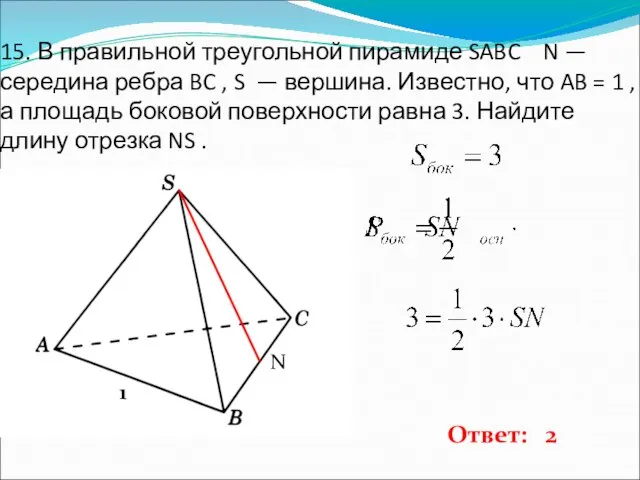
15. В правильной треугольной пирамиде SABC N — середина ребра BC , S — вершина. Известно, что AB = 1 , а площадь боковой поверхности равна 3. Найдите длину отрезка NS .
N
1
Ответ: 2

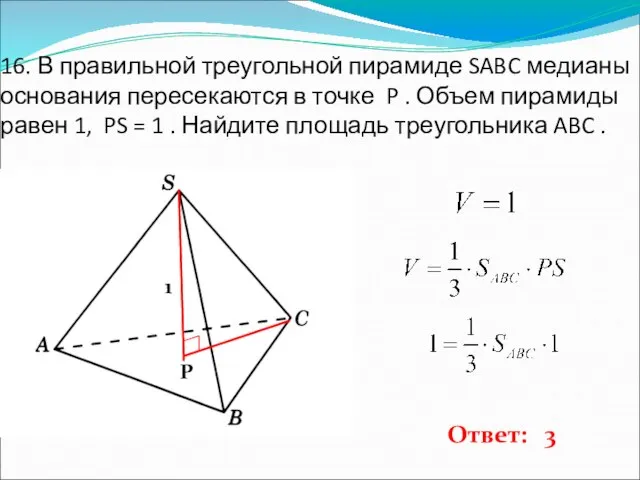
16. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке P . Объем пирамиды равен 1, PS = 1 . Найдите площадь треугольника ABC .
1
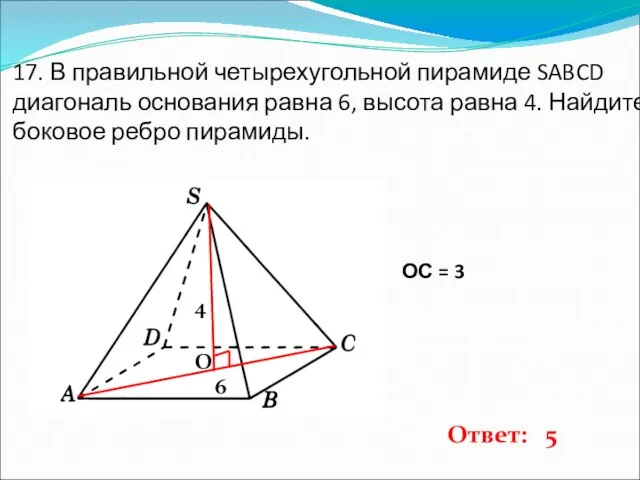
Ответ: 3

17. В правильной четырехугольной пирамиде SABCD диагональ основания равна 6, высота равна 4. Найдите боковое ребро пирамиды.
6
4
О
ОС = 3
Ответ: 5

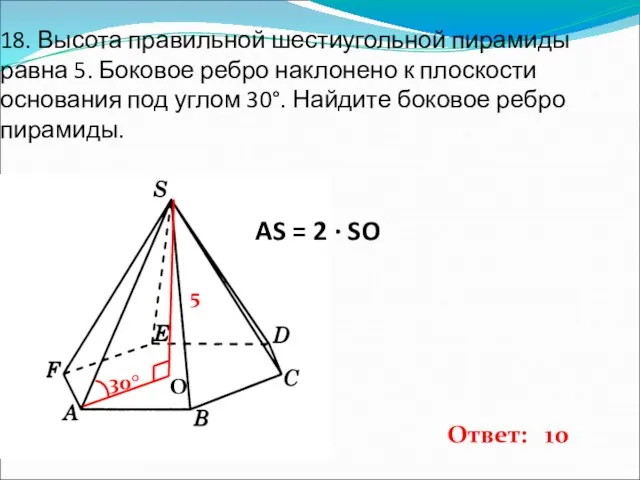
18. Высота правильной шестиугольной пирамиды равна 5. Боковое ребро наклонено к плоскости основания под углом 30°. Найдите боковое ребро пирамиды.
5
30°
О
AS = 2 · SO
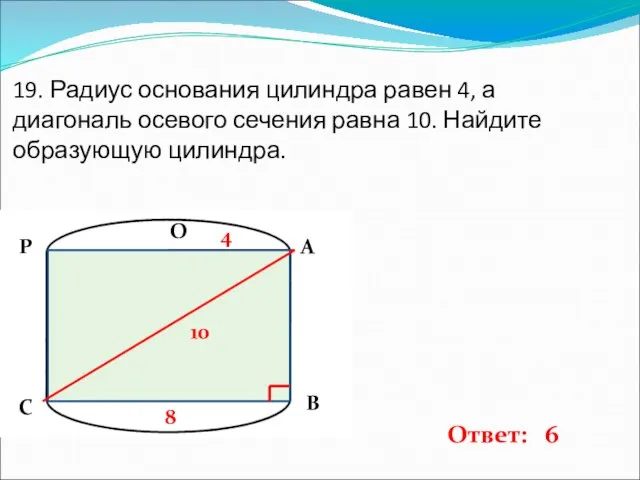
Ответ: 10

19. Радиус основания цилиндра равен 4, а диагональ осевого сечения равна 10. Найдите образующую цилиндра.
4
10
8
Ответ: 6
О
А

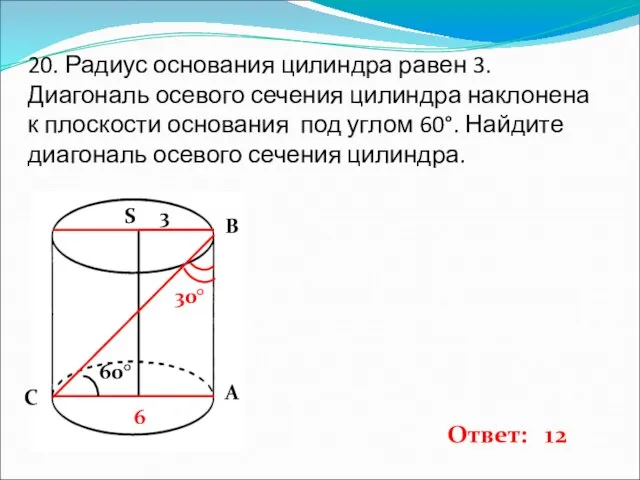
20. Радиус основания цилиндра равен 3. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 60°. Найдите диагональ осевого сечения цилиндра.
3
60°
6
30°
Ответ: 12
S
В
А
С

21. Площадь боковой поверхности цилиндра равна 2π, а диаметр основания — 1. Найдите высоту цилиндра.
1
0,5
H
R
Ответ: 2
О
А
В
S

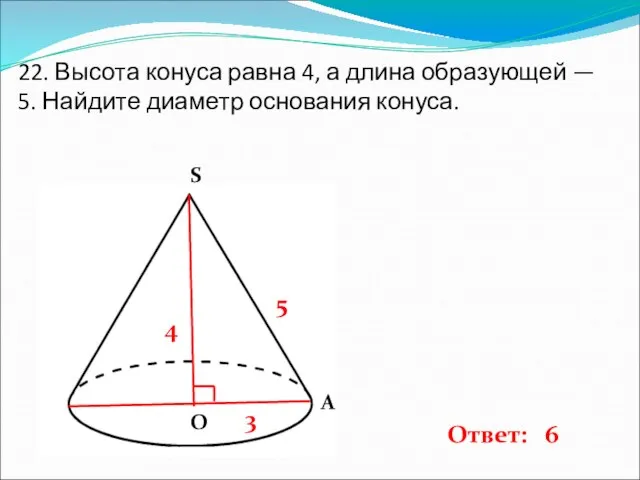
22. Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
4
5
3
S
O
A
Ответ: 6

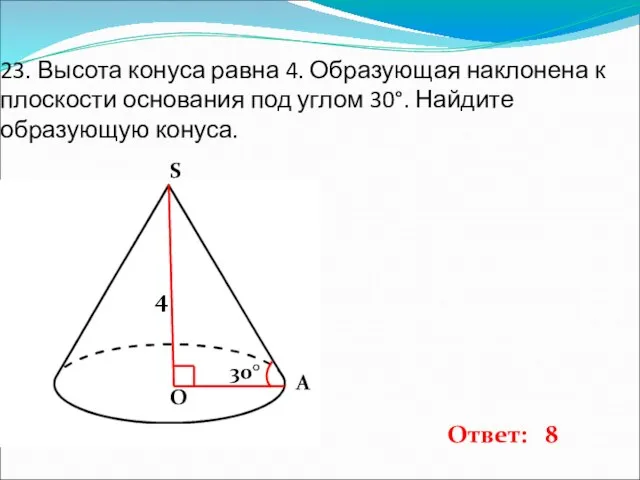
23. Высота конуса равна 4. Образующая наклонена к плоскости основания под углом 30°. Найдите образующую конуса.
4
30°
Ответ: 8
S
О
А

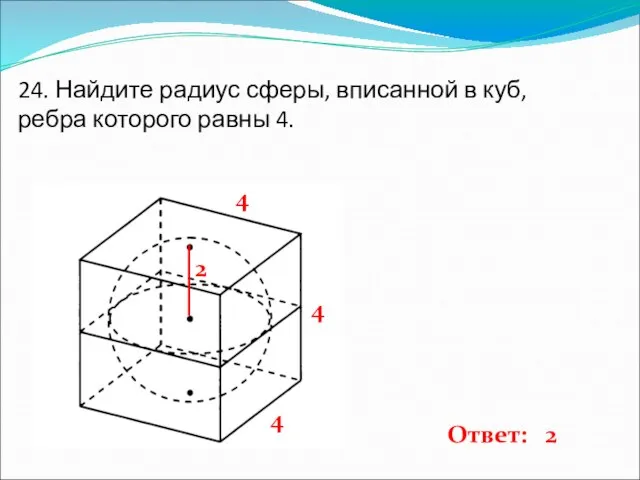
24. Найдите радиус сферы, вписанной в куб, ребра которого равны 4.
4
4
4
2
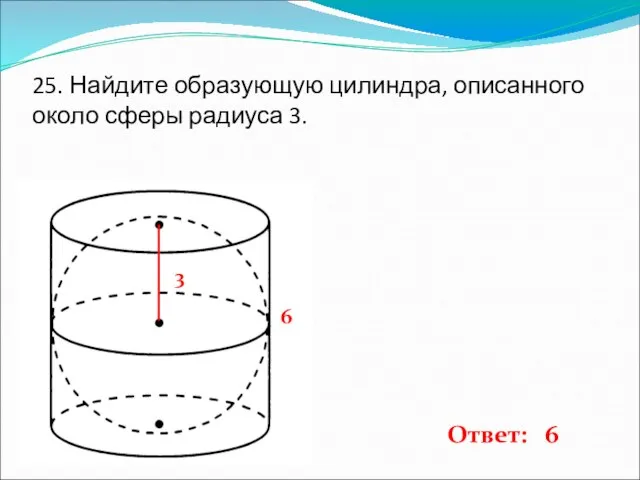
Ответ: 2

25. Найдите образующую цилиндра, описанного около сферы радиуса 3.
3
6
Ответ: 6

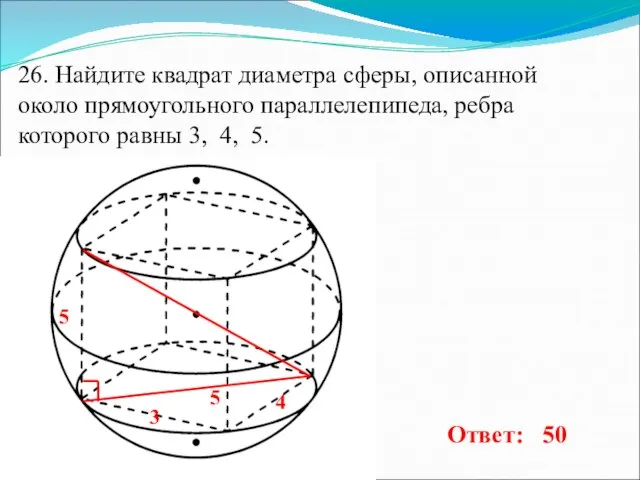
26. Найдите квадрат диаметра сферы, описанной около прямоугольного параллелепипеда, ребра которого равны 3, 4, 5.
3
4
5
5
Ответ: 50